滤正则序列与局部上同调

张英龙, 李思泽，2

(1.北京交通大学 理学院 北京 100044; 2.北京交通大学 轨道交通控制与安全国家重点实验室 北京 100044)

0 引言

深度(depth)在交换代数中是一个基本而又重要的概念，给出它的刻画具有十分重要的意义.文献[1]详细给出了深度的刻画和一些重要性质.其中,深度定义为极大正则序列的长度,由文献[1]知,不同的极大正则序列有相同的长度.

1 预备知识

文中R表示诺特环，M，N表示有限生成R模,I表示R的理想,p,q表示R的素理想,Z⊆Spec(R)是闭集.由于作者所使用的技术手段主要是局部化,所以有必要把如下的一个关于局部化的基本结果叙述出来.

事实上,本引理是文献[3]性质Ⅲ.6.8的直接推论.

2 滤正则序列的定义和刻画

定义1称x1,…,xn∈R为关于Z的长为n的M滤正则序列，如果

∀i∈[1,…,n],Supp(0:M/(x1,…,xi-1)Mxi)⊆Z.

注1(1)x1,…,xn∈R是关于Z的M滤正则序列当且仅当存在1≤i≤n，使得x1,…,xi-1是关于Z的M滤正则序列，且xi,…,xn是关于Z的M/(x1,…,xi-1)M滤正则序列；

证明现证明其逆否命题，即

⟸若x∈q,q=ann(m)∈AssR(M){Z}，则m∈0:Mx,因此m/1∈(0:Mx)q.由ann(m)=q知m/1在Mq中非零，所以(0:Mx)q≠0且q∈Spec(R){Z}.

现有如下两个断言:

(1)对任意的z∈R{p},都有zm≠0,ann(zm)⊆q;

(2)S={ann(zm)|z∈R{p}}中的极大元为R中的素理想.

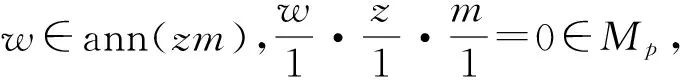
关于断言(2),用反证法.假设c∈R{p}使得ann(cm)为S中极大元,并假设ann(cm)不是素理想,则存在a,b∈R使得a∉ann(cm),b∉ann(cm),ab∈ann(cm).所以ann(acm)ann(cm),ann(bcm)ann(cm),故知ann(acm),ann(bcm)∉S.于是ac∈p,bc∈p,再由c∈R{p}知a,b∈p.

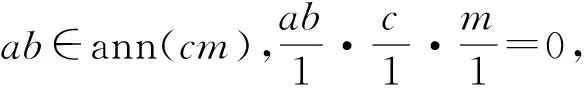
注2根据引理2,I中存在关于Z在的M滤正则元当且仅当I因此,由于M是诺特环R的有限生成模,由交换代数知识知AssR(M)是有限集,所以I中不包含关于Z在的M滤正则元当且仅当存在p∈AssR(M){Z},使得I⊆p.

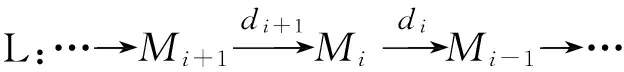
显然，L是关于Z的R模的拟正合序列当且仅当∀p∈Spec(R){Z},L是Rp模正合序列.

定理1设R是诺特环,M是有限生成R模,则下列条件等价：

(d)I中存在长度为n的关于Z的M滤正则序列.

证明(a)⟹(b)⟹(c)显然.

(c)⟹(d) 对n进行归纳证明.

(1)n=1.反证法.设I中不存在关于Z的M滤正则元,则由引理2知,存在p∈AssR(M){Z}，使得I⊆p.由R模正合列0→R/p→M可得,HomRp(k(p),Mp)≠0.另一方面,由p∈V(I)=Supp(N)可知,Np≠0由Nakayama引理知,Np/pRpNp是域k(p)上的非零向量空间.于是Homk(p)(Np/pRpNp,k(p))≠0.考虑合成同态Np→Np/pRpNp→k(p)→Mp.由R诺特,N有限生成知,(HomR(N,M))p≅HomRp(Np,Mp)≠0矛盾.故I中存在关于Z的M滤正则元.

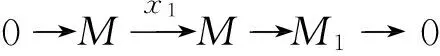
3 深度的定义和刻画

定义3定义M关于Z的相对I滤深度为包含在理想I中的关于Z的极大M滤正则序列的长度,记作depthZ(I,M).

(3)对于depthZ(I,M)是否无限及是否为零有如下的刻画：

(a)Supp(M)∩V(I)⊆Z⟺depthZ(I,M)=∞;

(b)AssR(M)∩V(I)Z⟺depthZ(I,M)=0.

⟸设depthZ(I,M)=∞,则任取p∈Supp(M)∩V(I){Z}.由于I⊆p,故依定义可知，I中关于Z的M滤正则序列都是Rp模Mp正则序列，由文献[1]知，这个长度≤depthRp(Mp)≤height(p)<∞.因此，必有Supp(M)∩V(I){Z}=∅,即Supp(M)∩V(I)⊆Z.

(b)由注(2)立得.

事实上,对于depthZ(I,M),还有

证明只需要对任意的正整数r证明下面两个结论的等价性即可.

(1)I中存在关于Z的长度为r的M滤正则序列;

(2)⟹(1) 对r进行归纳证明:

参考文献：

[1] Matsumura H. Commutative Algebra[M]. 2nd Ed. New York: The Benjamin/Cummings Publishing Company, 1980:95-114.

[2] Lü Rencai, Tang Zhongming. The f-depth of an ideal on a module[J]. Proceedings of the American Mathematical Society, 2001, 130(7): 1905-1912.

[3] Hartshorne R. Algebraic Geometry[M]. New York: Springer-Verlag, 1977: 235-236.

[4] Huneke C. Lectures on Local Cohomology[M]. Rhode Island: American Mathematical Society, 2008: 8-9.

[5] Weibel C A. An Introduction to Homological Algebra[M]. Cambridge: Cambridge University Press, 1994: 104-119.