多关系连接顺序选择与代价估计
冯凯平
0 前言
在关系数据库中,最难处理和优化的一个逻辑操作符是连接(JOIN),由于多个关系连接时可以有很多不同的顺序,因此对应于查询的执行计划的数目会随着该查询包含的关系个数呈指数级增长,当关系个数很多时,将导致搜索空间极度膨胀。[1]因此,当连接操作涉及多个关系时,需要考虑连接顺序。人们设计了多种连接顺序及方法,如遗传算法、模拟退火算法、蚁群算法、左偏树连接法等,其中左偏树连接其代价是较低的且容易实现。
1 连接顺序的选择
当对两个关系选择连接顺序时,一般来说将较小的关系先读入主存,这样可以较好地匹配来自另一个关系中的元组,当与另一个关系连接时,每次读入一个块,并将关系中的元组和已存入内存中的元组进行连接操作。
1.1 连接树
做如下符号约定:πL为投影(L为投影属性)、σC为选择(c为选择条件)、∞C为连接(c为连接条件)、×为关系的迪卡尔积、T(R)为关系R的元组数目、V(R,A)为关系R中属性A不同取值的种类数目。
假设有以下四个数据表,学籍表:XJ(姓名,年龄,专业,特质,…)、试题库表:ST(题号,适合专业,难度,…)、选课表:XK(课程,适用专业,姓名,…)、答题表:DT(考生姓名,题号,作答,用时,分值,…)。
实例1:查询专业为烹饪工艺、选修了“食品化学”课程的学生姓名。
Select b.姓名
From XK as a inner join XJ as b a.姓名=b.姓名
Where b.专业=”烹饪工艺”and课程=”食品化学”(1)
式(1)的逻辑代数树结构[2]。如图1所示:
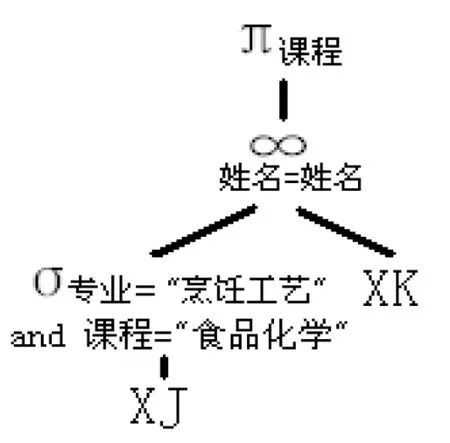
图1 式(1)的代数树
选择XJ作为第一个变元(左变元),其依据是,一个学生可以选择多门课程,如果规定每位学生必须选择一门以上的课程,那么关系XJ的规模必定小于XK,而且XJ又进行了σ年龄=20的选择操作,致使XJ的规模进一步缩小。所以选择XJ作为第一变元为最佳。
对于两个关系的连接,其树结构只有两种情形,原则上可以任意取一个关系作为第一变元。当关系多于两个时,如n个,树的形状数目T(n)按下式递归增长:[3][4]
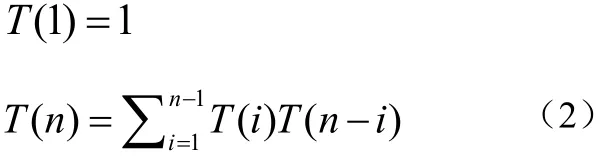
四个关系中其中的三种树结构,如图2所示:
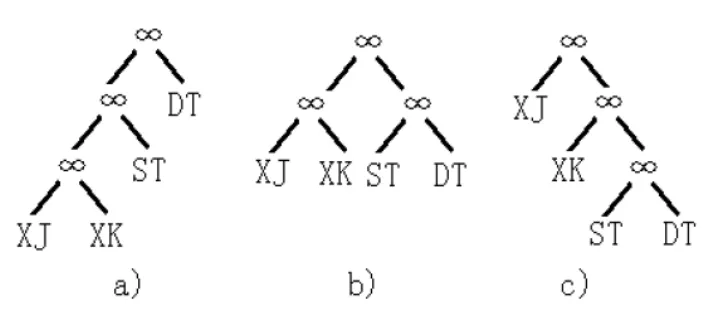
图2 四个关系的连接方法
把每一个关系(叶结点)放在树中不同的位置进行排序,共有4!=24种排序方法。当n=4时,T(4)=5,此时,总的树形结构共5*4!=120种。
1.2 左偏连接树
左偏树是一棵二叉树,图2a)中,所有的叶结点都在右方,是左偏树,根据各个变元排列顺序的不同,共有24种树形可供选择。图2c)则为右偏树,图2b)为紧密树。左偏树有以下两项优点:[3]
第一,查询计划的搜索可以用于较大的查询;
第二,基于左偏树查询算法的查询计划比其他种类的树结构的算法更加有效。
实际应用中,作为一个叶结点,中间还可以带有其他操作符号,如图1,左结点加入了选择操作。
考虑图2a)左偏树。假设4个关系规模的大小顺序是XJ、XK、ST、DT,以左变元开始建立树关系,其意义在于以树左方的变元优先存储在主存中。在进行XJ∞XK连接操作之前,首先将XJ存入内存,然后计算XJ∞XK并存储。用B表示缓冲区块,此时占用的内存缓冲区大小为B(XJ)+B(XJ∞XK)。由于XJ和XK是四个关系较小的,所以主存缓冲区应当能够容纳这些块。下一步计算XJ∞XK∞ST并存入主存中,现在XJ已无保留的必要,所以缓冲区块的大小为B(XJ∞XK)+B(XJ∞XK∞XT)。同理,当再加入DT的连接后不再保留XJ∞XK。缓冲区可以存储连接的最终结果。
如果采用图2c)右偏树,首先将XJ存入主存缓冲区,用于“建立关系”,紧接着将XK∞ST∞DT载入内存进行XJ的“关系试探”,但是要计算XK∞ST∞DT需要将XK放入缓冲区以建立关系,然后计算出ST∞DT作为XK的试探关系。但是ST∞DT需要先将ST读入缓冲区。现在内存中同时有XJ、XK、ST3个关系。此意味着如果要进行n个叶结点的右偏树连接,就必须先将n-1个关系同时读入内存中,增加了缓冲区数目。而左偏树任何时候最多每次连接仅需开辟两个缓冲区容纳两个关系即可。
如果一个连接在主存中只能获得有限个缓冲区,当缓冲区过多时,将增加磁盘访问次数、加重CPU及I/O时间开销,最终使得所有算法的性能降低。
2 多属性连接的代价估计
实例2:自适应型考试是一种新型的先进测试方式,它为学生选取的题目适应学生特质。现需查询所选择的题目适合本人专业,且题目难度与自身特质相适应的学生。以题目难度与特质相差0.3为判定标准。将特质与难度都分成30个等级区间(实际应用中会出现缺值)。其SQL表达式为:

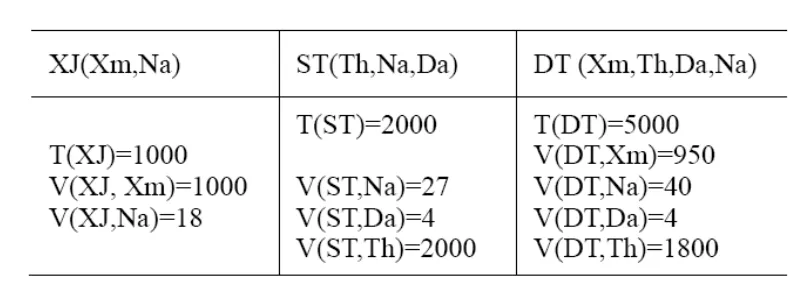
XJ和ST的T、V参数。根据其数据值,XJ与ST的连接概率做如下估计,如表1所示:

表1 XJ与ST的T、V参数表
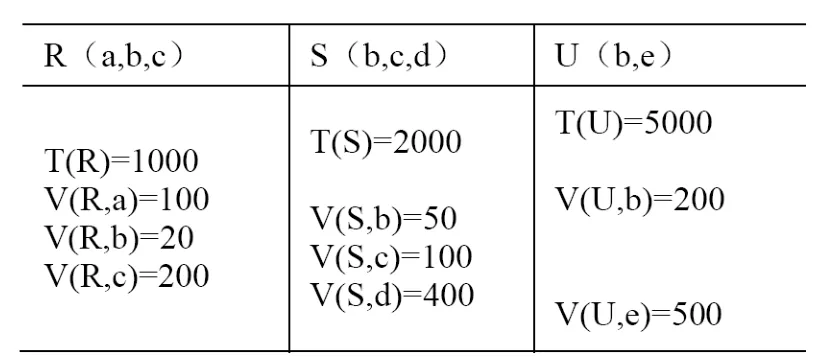
假设XJ中有一元组x,ST中有元组s,将属性“专业”和“适合专业”用Zy表示。如果V(XJ,Zy)≥V(ST,Zy),根据“值集包含”原理那么s的Zy必然出现在XJ中的诸Zy值之一。因此,x具有与s相同Zy的概率是1/V(XJ,Zy)。类似,如果V(XJ,Zy) 由此得知,在Zy上的相同概率是1/max(V(XJ,Zy),V(ST,Zy))。 同理,将学生“特质”和题目“难度”用Na表示,关于x和s在Na上取相同值的概率的方法应当是1/max(V(XJ,Na),V(ST,Na))。 由于Zy和Na值是独立的,元组在Zy和Na上相同的概率是这些因子之积。因此,源自XJ和ST的迪卡尔积T(XJ)·T(ST)元组中,在Zy和Na上匹配的期望值是:[4][5][6] 式(3)的最终估计值为1000*2000/(max(15,20)max(18,27))=3703个元组。 假设有n个关系R1、R2、……Rn,进行以下连接操作:S=R1∞R2∞…∞Rn。 假设属性A出现在k(1≤k≤n)个Ri中,在此k个关系中,值的集合的个数(即V(Ri,A)的各个值,其中i=1,2,…k)满足v1≤v2≤…≤vk,次序从最小到最大。假设从每个关系中选一个元组,所选的元组在属性A上相同的概率是多少? 考虑从具有最小数目的A值v1的关系中选取的元组t1。根据值集包含原理,这v1个值中的每一个值是在其他具有属性A的关系中所发现的A值中。考虑属性A上有vi个值的关系。它所选的元组ti在属性A上与ti相同的概率是1/vi。由于这个结论对于所有i=2,3…,k均为真,因此所有k个元组在A上相同的概率是积1/v2v3…vk。由此可得到以下规则: 从每个关系中元组数的积出发,然后,对于至少出现两次的属性A,除以除了V(R,A)中最小值之外的所有值。[3][4] 实例3:假定有3个关系的T、V统计值。考虑连接R(a,b,c)∞S(b,c,d)∞U(b,e),如表2所示: 表2 R、S与U的T、V参数表 为估计此连接大小,先将3个关系的T值做积操作,即1000×2000×5000。接着,查找那些出现多于两次的属性,它们是b出现3次,c两次。将积除以V(R,b)、V(S,b)、V(U,b)中较大的两个值,它们是50和200。最后,再除以V(R,c)、V(S,c)中较大的一个,即200。其估计结果是: 1000×2000×5000/(50×200×200)=5000 实例4有以下3个关系: 将XJ、ST、DT3个关系中具有同类性质的属性特质、难度、分值用符号Na表示;属性姓名、考生姓名用Xm表示;作答、答案用Da表示;题号用Th表示。某次考试后3个关系的属性值,如表3所示: 统计中等特质水平(16-25)的考生作答较大难度题目(25-30)的得分情况。 作如下假设:没有特低特质(1-12)区间的考生、没有特低难度(1-3)区间的试题。 按左偏树进行连接操作: Select a.姓名,c.分值 From Xs as a,Ti as b,Dt as c Where a.姓名=c.考生姓名and b.题号=c.题号and b.答案=c.作答and(b.难度>="25"and b.难度<="30")and(a.特质>="16"and a.特质<="25") 统计它们之间连接(即S=Xs ∞Ti∞Dt)之后的大小: 多连接查询的优化是一个复杂问题。本文通过应用实例分析,重点阐述了基于左偏树平均值统计的数据查询优化过程中连接操作代价的估计方法。这种算法通过各个关系之间的大小顺序作为选择连接下一个关系的依据,使得估计过程简单、明了。在关系数目不是太多时是一种比较好的选择。诚然,当连接关系较多时,可以考虑其他估计方法,如遗传统计法、群蚁统计法等。 [1]王莹,徐鑫.GAAA算法在数据库多连接查询优化中的研究应用[J].云南师范大学学报.2011,31(1),54-56. [2]伍军云,徐少平,林振荣等.一种新的关系数据库查询优化方法[J]计算机与现代化.2006,7,33-35. [3]Hector Garcia-Molina,Jeffrey D.Ullman,Jennifer Widom.Database System Implementation[M].Palo Alto,California:Stanford University,2001,3. [4]郭聪莉,朱莉,李向.基于蚁群算法的多连接查询优化方法计[J].计算机工程.2009,35(10),173-175. [5]彭建平,王变琴.再探多连接查询优化方法[J].中山大学学报.2001,40(2),27-30. [6]李志伟.基于贪婪策略的分布式数据库查询优化研究[j]计算机工程与设计.2010,31(17),3838-3840.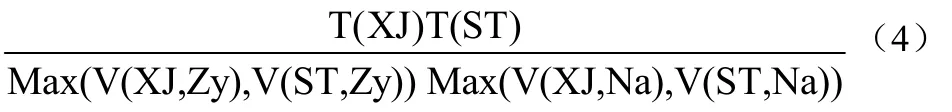
3 多个关系连接的代价估计
3.1 多关系连接代价估计方法
3.2 多关系连接代价估计实例分析
4 结束语

