基于振动响应的耦合杆系统损伤识别*

吕中荣，王文洁，徐伟华，刘济科

(中山大学力学系，广东 广州 510275)

近年来,利用测量的振动响应进行结构损伤识别是国内外研究的热点之一。 理论上讲，结构局部损伤的产生使得在该区域的结构刚度有所下降,结构的振动响应及模态参数等( 模态频率、模态振型、模态阻尼等) 也将随之而改变。因此，通过研究结构的振动响应或振动特性的改变,就能判断结构发生损伤与否,并进一步确定损伤的位置和程度。一般来说，工程结构的损伤识别可以分为以下4个步骤[1]: ①判断结构是否发生损伤; ②确定损伤的位置; ③确定损伤程度; 以及④结构发生损伤后的寿命预估。基于振动的结构损伤识别法具有非破坏性、方便、快速和廉价的优点,已经广泛应用到梁类、板类等结构的损伤识别中[2-11]。

本文对具有相近频率的强耦合杆和相重频率的弱耦合杆系统的损伤识别问题进行研究。首先建立了强耦合杆和弱耦合杆系统的有限元运动方程。利用状态空间法计算系统在外激励下的响应。将杆的局部损伤模拟为单元抗拉刚度的减少。推导了响应对杆单元抗拉刚度的灵敏度。并利用此响应灵敏度进行杆的局部损伤识别。对耦合杆系统单一和多个局部损伤进行了识别，研究了人工噪声对识别精度的影响。算例表明，本文方法能够有效地识别出耦合杆的局部损伤。

1 正问题

如图1所示的两跨连续杆系统在跨中通过弹簧耦合在一起，当弹簧常数kt较大时，系统为弱耦合系统，当弹簧常数kt较小时，系统为强耦合系统。通过有限元法离散，系统的强迫振动方程可以写成如下形式：

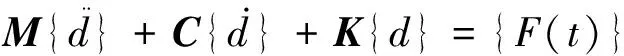
(1)

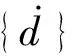
应用状态空间法，式(1)改写为

(2)

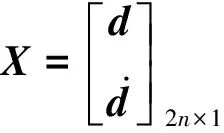
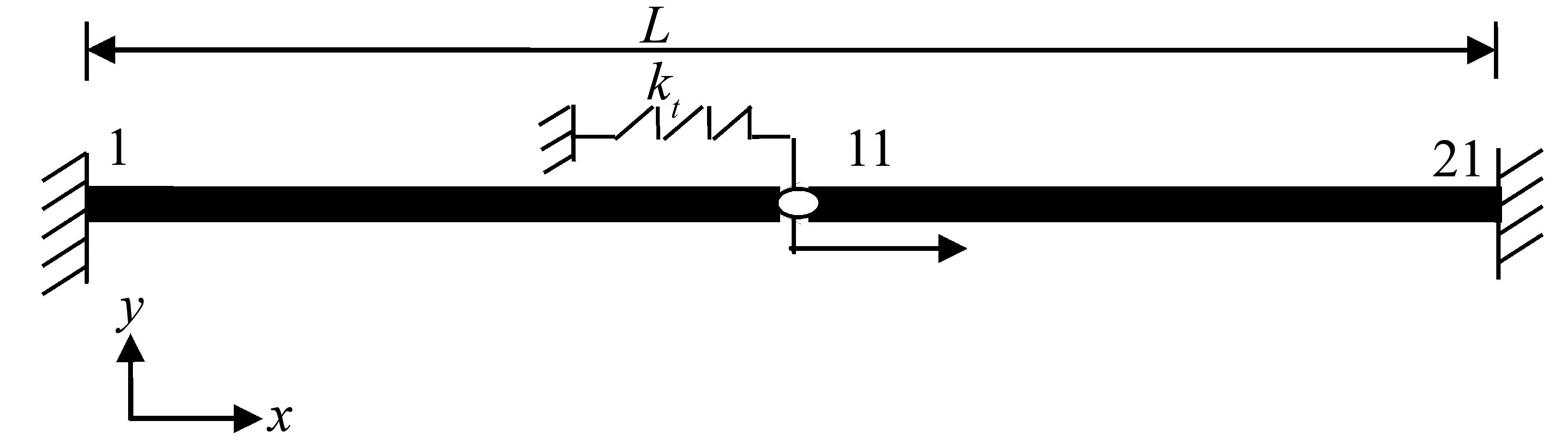
图1 两端固支耦合杆系统(1,11,21为有限元节点编号)

利用指数矩阵法，微分方程(2)转化为如下离散的形式

(3)

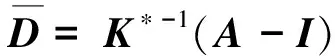
给定外激励{F(t)}，系统的振动响应可以由式(2)计算得到。

2 反问题

2.1 振动响应对损伤参数的灵敏度

在反问题中，利用基于时域响应灵敏度的有限元模型修正法来进行杆的局部损伤识别。在本文中，将杆局部损伤模拟为单元抗拉刚度的减少，并忽略损伤引起结构质量的改变。对式(2)中结构的损伤参数，如第i个单元的抗拉刚度EAi求偏导数，可得

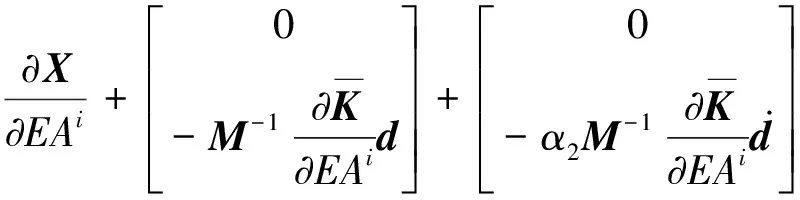
(i=1,2,…,n)

(4)

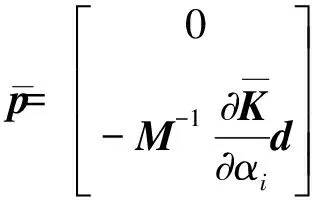
(5)

式(5)的离散形式为

(6)

位移和速度响应对抗拉刚度的灵敏度可直接从式(5)求得，加速度响应灵敏度可以由速度响应灵敏度微分一次获得，进一步便可形成响应灵敏度矩阵。

2.2 结构损伤参数的识别

识别问题可以表达为：寻求抗拉刚度向量{EA}，使得计算出来的响应，如加速度响应与测量的响应最好地匹配，也就是

(7)

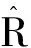
识别方程可以表示为，

{δz}=S{δEA}

(8)

抗拉刚度增量向量δ{EA}可以从阻尼最小平方法获得[13]

δ{EA}=(STS+λI)-1STδ{z}

(9)

其中λ是正则化参数，本文应用L曲线方法获得最优的正则化参数λ[14]。

修正后的抗拉刚度向量为

{EA}={EA0}+{δEA}

(10)

其中{EA0}为没有损伤时系统的抗拉刚度向量。

3 数值计算

如图1所示的耦合悬臂杆系统，经有限元离散为20个均匀杆单元。假定系统参数为：杆的杨氏模量E0=200 GPa，密度ρ=7 860 kg/m3，杆的总长L为10 m，横截面面积为0.000 1 m2。系统为强耦合系统时取kt=108N/m，系统为强耦合系统时取kt=1010N/m，假定外激励为一个三角形冲击力，其大小为

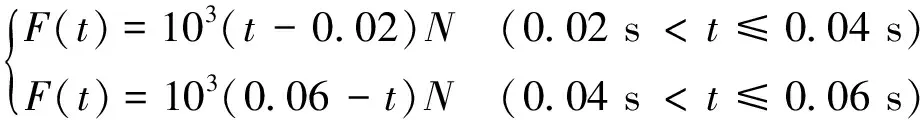
该力从初始时刻t=0.02 s开始，到0.06 s结束，沿轴正方向作用在杆第11号节点上。假定系统前2阶模态的阻尼系数均为0.01，计算响应时，时间步长取为0.000 2 s。

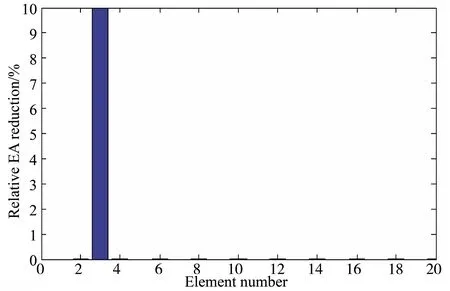
图2 强耦合杆系统单一损伤的识别(无噪声)

3.1 强耦合系统损伤识别

工况1：单一损伤的识别。

首先研究单一损伤的识别，假定系统的第3个单元的抗拉刚度减少10%来模拟局部损伤。损伤识别中，利用位于第5、 10和15个节点上的3组加速度响应1.0 s的数据来进行识别。在这个工况中，不考虑测量噪声的影响。经过17次迭代后，识别结果如图2所示。该图表明，第3个单元上的局部损伤成功地识别出来了，并且在其他单元上没有出现误判的情况。表明本文方法能够成功地识别出强耦合杆系统的单一局部损伤。

工况2：多损伤的识别。

假定强耦合杆系统第3号和第15号单元的抗拉刚度分别减少10%、5%来模拟局部损伤。用于识别损伤的加速度响应同工况1。在这个工况中也不考虑测量噪声。经过19次迭代后，识别结果如图3所示。该图表明，第3和第15号单元上的局部损伤成功地识别出来了，该算例表明本文方法能够有效识别出强耦合杆系统的多个局部损伤。

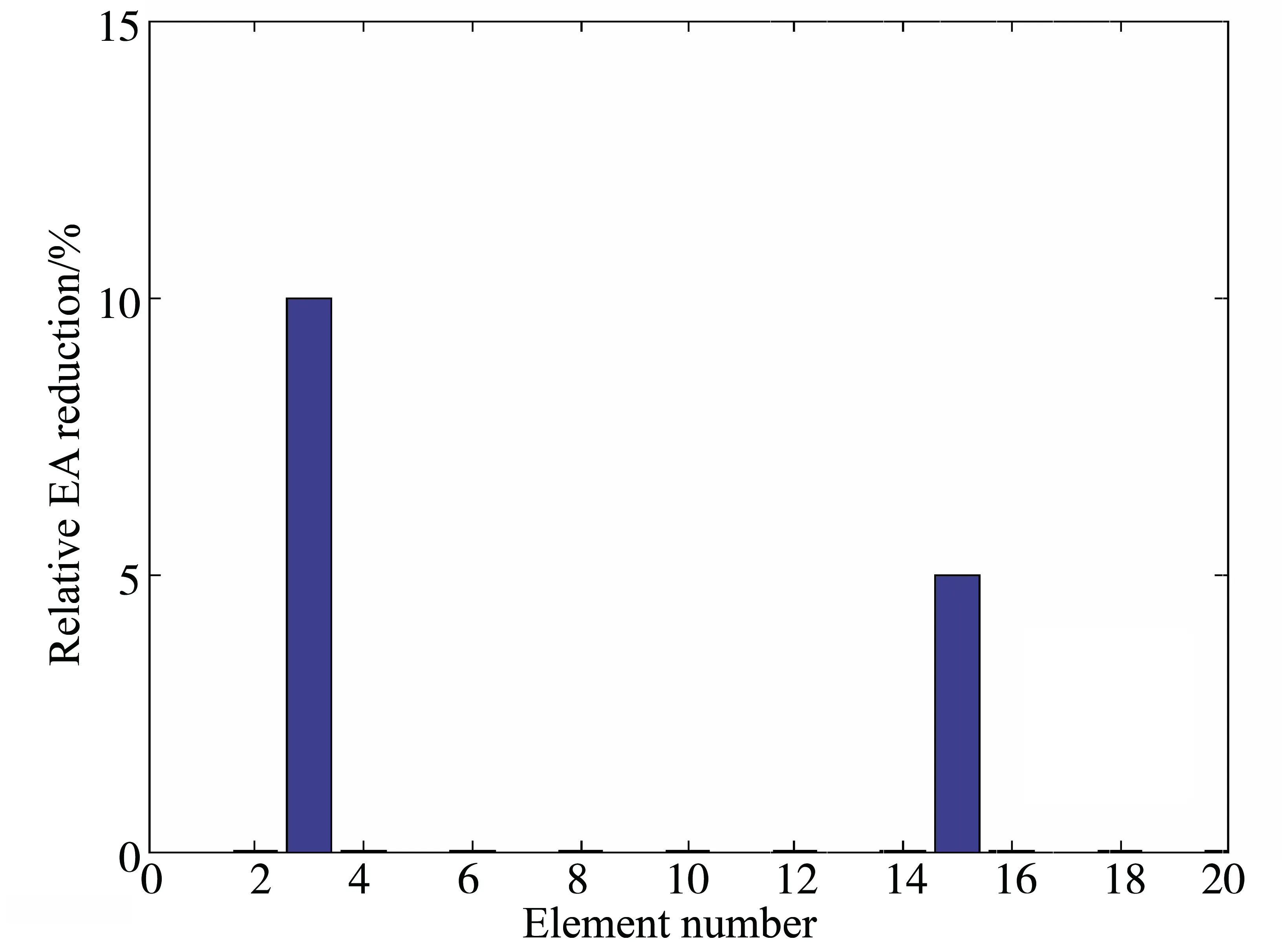
图3 强耦合杆系统多损伤识别(无噪声)

工况3：测量噪声的影响。

这个工况中研究测量噪声对损伤识别结果的影响，重新考虑工况2。有人工模拟噪声的加速度响应可表示如下

*Noise*

(12)

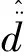
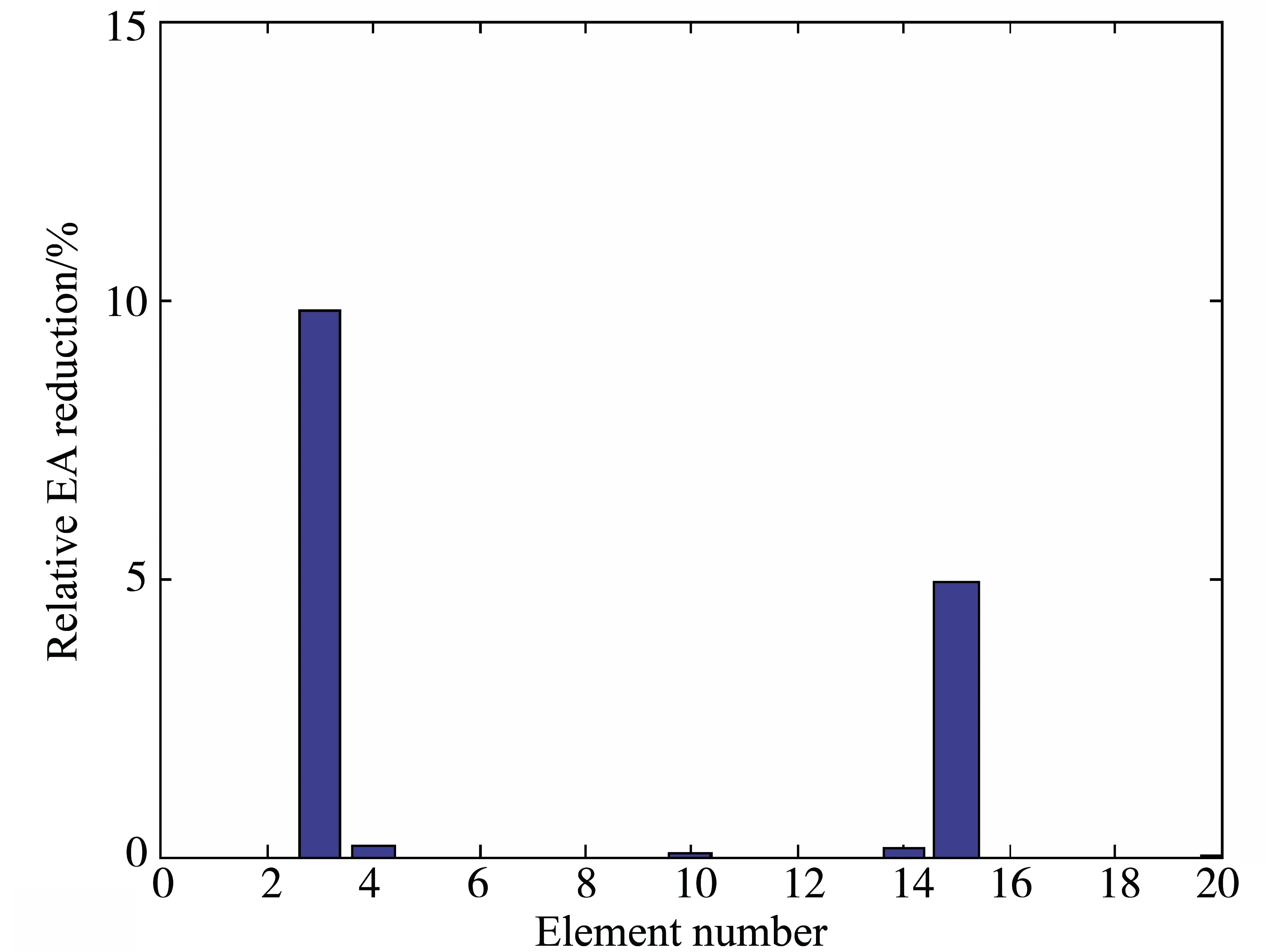
图 4 强耦合杆系统多损伤识别(10% 噪声水平)

3.2 强耦合系统损伤识别

工况4：多损伤的识别。

这里研究弱耦合杆系统的多损伤识别，假定系统第3、15号单元的抗拉刚度分别减少10%、5%来模拟局部损伤。用于识别损伤的加速度响应同上一个工况。在这个工况中也不考虑测量噪声。经过19次迭代后，识别结果如图5所示。该图表明，第3和第15号单元上的局部损伤成功地识别出来了，识别的最大误差约为0.1 %，表明本文方法能够成功地识别出弱耦合系统的多个局部损伤。

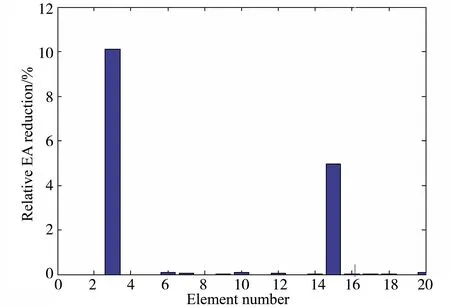
图5 弱耦合杆系统多损伤识别

工况5：测量噪声的影响。

这个工况中研究测量噪声对损伤识别结果的影响，重新考虑工况4。同样在计算响应中增加10%人工噪声来模拟实际的测量噪声对识别结果的影响。经过24步迭代计算后，识别结果图6所示。该图表明，在10%的噪声水平下，2个局部损伤也被成功地识别出来，最大误差不到0.5%，这进一步表明本文方法对测量噪声不敏感。

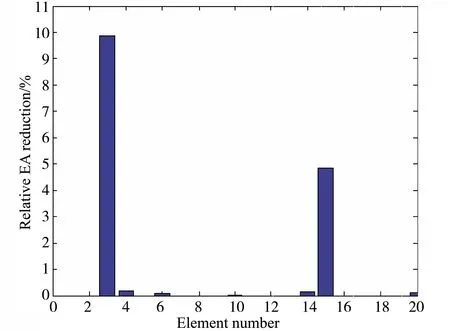
图6 弱耦合杆系统多损伤识别(10% 噪声水平)

4 结 论

提出了基于时域响应的有限元模型修正法的损伤识别方法对耦合杆系统的局部损伤进行识别。本文方法能有效识别具有相近频率和相重频率特征的耦合杆系统的局部损伤。主要结论如下：

1) 需要利用加速度测点的数目较少,本文中只需要利用三个测点上的加速度响应就能成功识别出耦合杆系统的局部损伤。

2) 损伤的定位和损伤程度的识别可以达到较好的精度要求，且计算量小,识别速度快。

3) 对测量噪声不敏感的，具有一定的工程应用潜力。

参考文献：

[1]RYTTER A.Vibration based inspection of civil engineering structures [D].Department of Building Technology and Structural Engineering,University of Aalborg.1993.

[2]WAHAB M M A,ROECK G D.Damage detection in bridges using modal curvatures: application to real damage scenario[J].Journal of Sound and Vibration,1999,226(2): 217-235.

[3]YANG Q W,LIU J K.A coupled method for structural damage detection [J].Journal of Sound and Vibration,2006,296: 401-405.

[4]朱宏平,张源.基于自适应神经网络的结构损伤检测 [J].力学学报，2003,35(1): 110-116.

[5]LAW S S,LI X Y,LU Z R.Structural damage detection from wavelet coefficient sensitivity with model errors [J].Journal of Engineering Mechanics-ASCE,2006,132(10):1077-1087.

[6]杨秋伟,刘济科.结构损伤识别的柔度灵敏度方法[J].中山大学学报:自然科学版,2010,49(1): 16-19.

[7]宋雨,项贻强,徐兴.基于结构振动的桥梁损伤检测 [J].振动、测试与诊断,2005,25(3): 222-226.

[8]刘济科,汤凯.基于振动特性的损伤识别方法的研究进展[J].中山大学学报:自然科学版,2004,43(6): 57-61.

[9]孙宗光,高赞明,倪一清.基于神经网络的桥梁损伤位置检测 [J].工程力学,2004,21(1): 43-47.

[10]WU D,LAW S S.Damage localization in plate structures from uniform load surface curvature [J].Journal of Sound and Vibration,2004,276(1/2): 227-244.

[11]刘济科,杨秋伟,邹铁方.结构损伤识别中的模型缩聚问题[J].中山大学学报:自然科学版,2006,45(1): 1-4，8.

[12]BATHE K J.Finite element procedures in engineering analysis [M].New Jersey:Prentice Hall,1982.

[13]TIKHONOV A M.On the solution of ill-posed problems and the method of regularization [J].Soviet Mathematics,1963,4:1035-1038.

[14]HANSEN P C.Analysis of discrete ill-posed problems by means of the L-curve [J].SIAM Review,1992,34(4): 561-580.