改进Z源逆变器三载波PWM策略

李军军，王世明，黄有方，匡兴红，杨琛

(1.上海海洋大学工程学院，上海 201306;2.上海海事大学科学研究院，上海 201306)

0 引言

相对于其他类型的逆变器［1－2］，Z 源逆变器［3］具有可实现升降压变换以及逆变器桥臂可以直通等优点，在新能源发电领域具有广阔的应用前景［4－7］.文献［8］提出一种改进Z源逆变器，能大大减小Z网络电容电压应力并具有内在的抑制启动冲击电流的能力，从而可以使用低压电容以减小系统的体积和成本、增加可靠性［9］.

对于三相Z源逆变器，目前主要有3种控制策略［10－12］:简单升压控制、最大升压控制、最大恒定升压控制，这些控制策略中升压因子与调制度相互关联.文献［13］提出一种双载波脉冲宽度调制(Pulse Width Modulation，PWM)策略，可使升压因子独立于调制度，但部分直通零状态在非零矢量作用时间加入，会改变原来的PWM波形，增加输出谐波.本文提出一种三载波PWM策略，通过3个三角波载波与三相调制信号比较控制6个功率器件，可以使升压因子独立于调制度，并且不改变原来的PWM波形.分析表明，采用该调制策略时，改进Z源逆变器电容电压应力和功率器件电压应力均低于传统控制策略.将该方法应用于改进Z源逆变器，可获得较好的控制效果.

1 改进Z源逆变器

改进Z源逆变器［8］拓扑见图1.假设Z网络对称，即 L1=L2，C1=C2，则 VC1=VC2=VC，vL1=vL2=vL，且有

式中:直通占空比D0=T0/T，T0为一个开关周期中的直通时间.VC小于传统Z源逆变器电容电压，有利于减小电容的体积并节约成本.

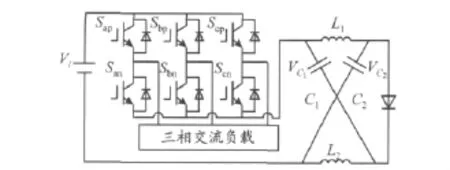
图1 改进Z源逆变器拓扑

升压因子

假设逆变器的调制度为M，则电压增益

因此

逆变桥两端的峰值电压为

逆变器输出的相电压峰值可以表示为

2 三载波PWM策略

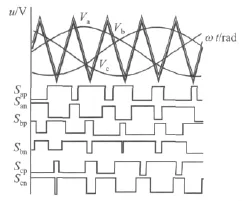
图2 双载波PWM波形

文献［13］提出一种双载波PWM策略，通过3个正弦调制波Va，Vb，Vc与两个高频三角波载波信号比较控制6个功率器件，见图2.图2中一个载波没有直流偏置电压(如粗实线三角波)，调制波Va，Vb，Vc与其比较之后获得的脉冲波控制图1中上面的3个功率器件 Sap，Sbp，Scp;另一个载波存在正的直流偏置电压(如细实线三角波)，调制波与其比较后获得的脉冲波控制图1中下面的3个功率器件 San，Sbn，Scn.直通时间即由 Sap与 San，Sbp与Sbn，Scp与Scn的错时通断产生.这种方法在调制度M不变时，可以通过调节载波的直流偏置电压改变升压因子B，从而调节电压增益G，具有M与B相互独立的优点.另外，由于每个直通时间内只有一相桥臂的两个功率器件同时闭合，该方法较其他方法的开关损耗小.

但这种方法也有输出电压总谐波畸变率较高的缺点.在载波的1/2个周期内，3个调制波Va，Vb，Vc与其中一个载波有3个交点，这3个交点若Va＞Vb＞ Vc，则 Sap与 San，Sbp与 Sbn错时通断产生的直通时间不属于传统零矢量作用时间.这会改变传统PWM输出的三相电压波形，增加输出电压的总谐波畸变率.

图3 三载波PWM波形

本文采用3个载波:载波1不叠加直流偏置电压，载波2和3分别在载波1的基础上叠加正直流偏置电压Voff和负直流偏置电压 － Voff，见图3.在载波1的1/2个周期中，3个调制波与载波1必有3个相交点，这 3个相交点若 Va＞Vb＞Vc，则:Va与载波3比较获得Sap，与载波1比较获得San;Vb与载波1比较获得Sbp和Sbn;Vc与载波1比较获得Scp，与载波2比较获得Scn.这样，Sbp与Sbn不存在错时通断，Sap与 San，Scp与 Scn存在错时通断，直通时间由这种错时通断产生.这两处的直通时间都在传统零矢量作用时间加入，与传统方式相比零矢量作用时间没有变化，因此不会改变输出电压PWM波形.

在M不变时，同样可以通过调节载波的直流偏置电压Voff改变B，从而调节G;每个直通时间内，同样只有一相桥臂的两个功率器件同时闭合.因此，该方法也具有双载波PWM中M与B相互独立、开关损耗小的优点.

若载波1幅值为Vt，则有

由式(2)有

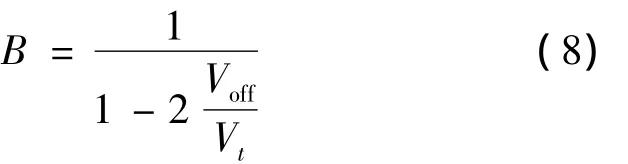
由式(3)有

一般要求 B＞0，所以D0＜0.5，因此要求 Voff/Vt＜0.5.Voff越大，B 越大，在一定的调制度M下G越大.当M=1时，G与Voff/Vt的关系见图4.

为尽量避免调制波与三载波不全相交的情况，调制波也采取3次谐波注入［14］的方法.

设A相调制波表达式为

图4 电压增益与Voff/Vt的关系

注入1/6倍3次谐波后，A相调制波为

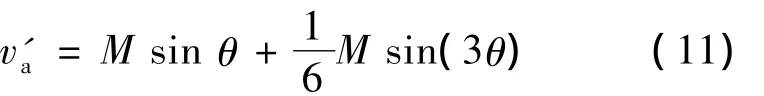
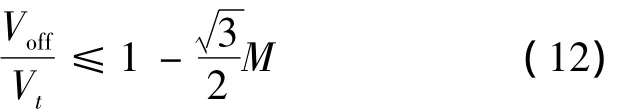
3 功率器件电压应力

3.1 输入电压相同

由式(5)可知功率器件电压应力为

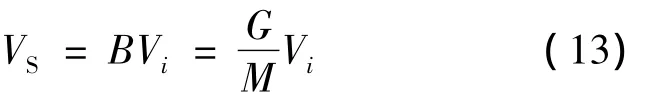
可见当输入电压相同时，可用升压因子的大小比较功率器件电压应力.改进Z源逆变器采用三载波PWM时，升压因子用B3C表示，即

改进Z源逆变器采用简单升压法、最大升压控制、最大恒升压控制的升压因子分别用BSB，BMB，BMCB表示，由文献［8，10－14］可知

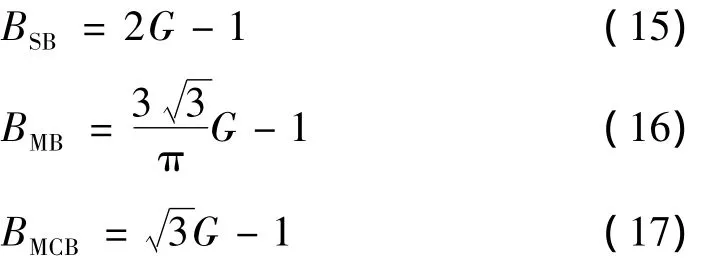
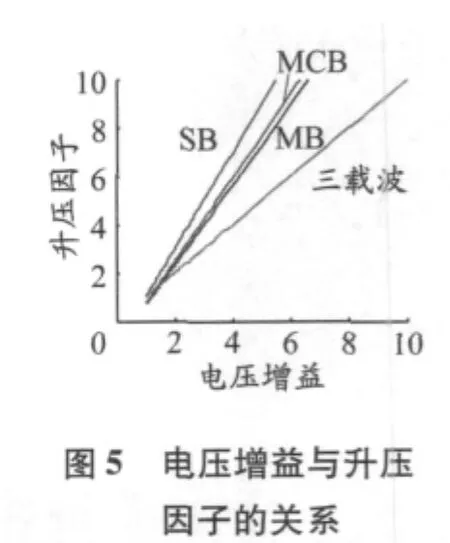
M=1时，简单升压法、最大升压控制、最大恒升压控制、三载波PWM升压因子与电压增益之间的关系见图5.图中SB，MB，MCB，三载波分别表示简单升压控制、最大升压控制、最大恒升压控制、三载波PWM控制.其中三载波PWM方法中，通过调节Voff/Vt来调节G的大小.为便于与文献［13］和［14］的类似图形比较，图5～8中G的范围都取0～10.

3.2 输出电压相同

由式(6)，(14)～(17)可得，输出电压相同时，简单升压法、最大升压控制、最大恒升压控制、三载波PWM下功率器件电压应力分别为

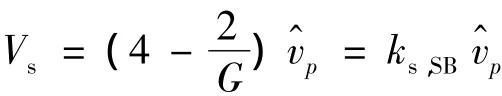
式中:ks，SB，ks，MB，ks，MCB，ks，3C分别为这 4 种控制下的功率器件电压应力因子，

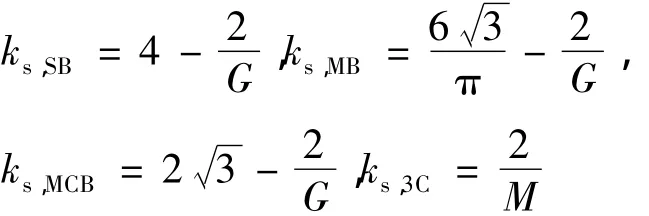
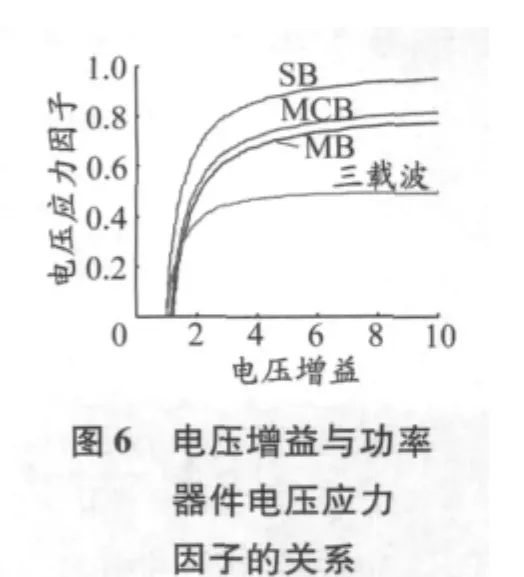
当M=1时，这几种控制方法功率器件电压应力因子与电压增益之间的关系见图6.

4 电容电压应力

4.1 输入电压相同

由式(1)～(4)可得，改进Z源逆变器电容电压应力为

简单升压法、最大升压控制、最大恒升压控制、三载波PWM下的电容电压应力分别为

即这几种控制下的电容电压应力因子为

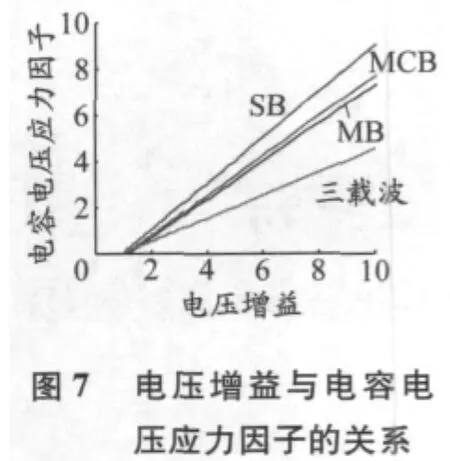
当M=1时，这几种控制下的电容电压应力因子与电压增益之间的关系见图7.

4.2 输出电压相同

由式(6)，(19)～(22)可得，输出电压相同时，简单升压法、最大升压控制、最大恒升压控制、三载波PWM下功率器件电压应力分别为

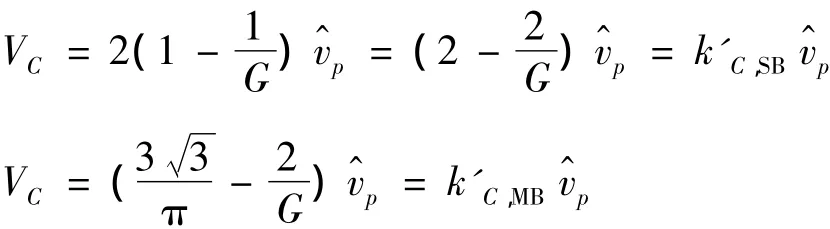
式中:k'C，SB，k'C，MB，k'C，MCB，k'C，3C分别为这 4 种控制下的功率器件电压应力因子，

当M=1时，这几种控制下的电容电压应力因子与电压增益之间的关系见图8.

5 仿真

通过仿真比较输出电压、输出电流的有效值及总谐波畸变率，以验证第2节关于本文方法输出PWM波形的分析.

5.1 Z源逆变器仿真

图9 线电压、线电流波形

对Z源逆变器采用双载波PWM、三载波PWM进行仿真，以验证本文方法的有效性.仿真参数为:C1=C2=1 000 μF，L1=L2=3 mH，调制波频率为50 Hz，载波频率为5 kHz，调制度M=0.8，输入电压Vi=150 V，采用三相阻感负载，每相为 50 Ω与10 mH串联.文献［13］中 Voff/Vt=0.15，则升压因子B=1.5Voff/Vt=0.225，为使升压因子与其一致，这 里 Voff/Vt=0.225(满足第2节对 Voff/Vt的要求).采 用MATLAB/Simulink搭建模型仿真，获得的线电压、线电流波形见图9.

线电压峰值理论计算值为272.73 V;本文仿真结果为272.19 V，与理论值十分接近.三载波PWM获得的线电压、线电流与文献［13］双载波PWM比较见表1(文献［13］中线电压有效值、峰值理论计算值为154.3，267.2 V是不对的).

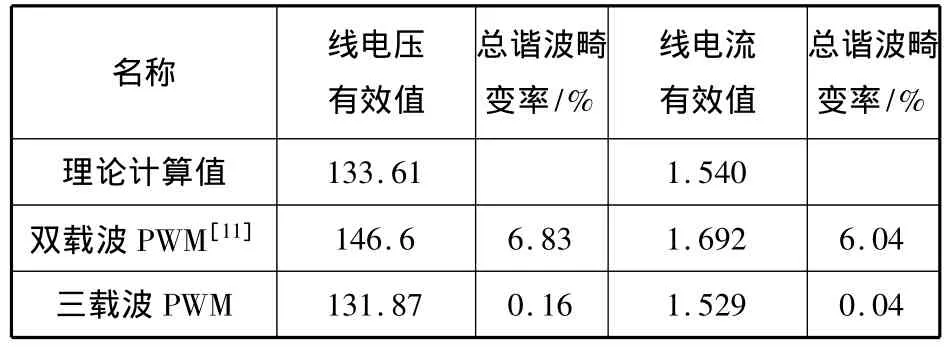
表1 线电压、线电流比较

经傅里叶分析，线电压、线电流基波及各次谐波幅值见图10.

由表1和图10可见，三载波PWM在Z源逆变器上效果较佳，明显优于双载波PWM.

图10 线电压、线电流频谱分析

5.2 改进Z源逆变器仿真

在改进Z源逆变器中采用三载波PWM，参数设置同第5.1节.功率器件电压应力、电容电压应力见图11.功率器件电压应力、电容电压应力理论计算值 为 272.73，61.36 V;仿真获得的这两个电压应力为 272.82，61.01 V，与理论值十分接近.

线电压、线电流理论计算值、有效值及总谐波畸变率与第5.1节一样，线电压和线电流有效值分别为131.87 V和1.529 A，线电压总谐波畸变率和线电流总谐波畸变率分别为0.16%和0.04%.可见三载波PWM是一种较好的控制策略.

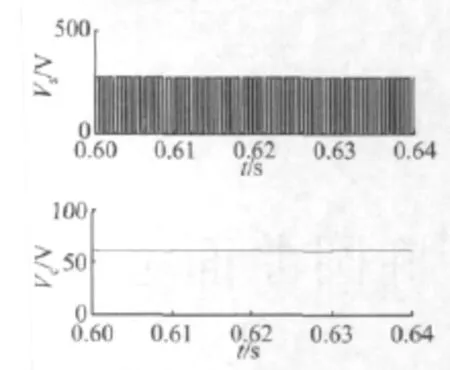
图11 电压应力

6 结束语

为使Z源逆变器升压因子与调制度相互独立，且不改变传统PWM输出波形，提出一种三载波PWM策略.分析表明该方法可以减小改进Z源逆变器功率器件电压应力、电容电压应力.Z源逆变器及改进Z源逆变器仿真结果显示，该方法是一种较好的控制策略.

［1］夏永明，索志民，王洋，等.用于太阳能光伏并网发电的五电平逆变器［J］.上海海事大学学报，2011，32(2):56－60.

［2］XU Bowei，LI Junjun.Harmonic reduction for cascaded multilevel inverters using modified PSO［J］. 上海海事大学学报，2012，33(1):85－90.

［3］PENG F Z.Z－source inverter［C］//IEEE Industry Applications Conf Pittsburgh，PA，USA，2002:775－781.

［4］KULKA A，UNDELAND T.Voltage harmonic control of Z－source inverter for UPS applications［C］//13th Int Power Electron ＆ Motion Contr Conf，Poznań，Poland，2008:672－277.

［5］BAKAR M S，RAHIM N A，GHAZALI K H.Analysis of various PWM controls on single－phase Z－source inverter［C］//Proc 2010 IEEE Student Conf on Res ＆ Dev，Putrajaya，Malaysia，2010:448－451.

［6］CHANDRUDU K R，RAJU P S.Comparison of Z－source inverter fed induction motor with traditional source inverter systems［J］.Res J Applied Sci，Eng ＆ Technology，2011，3(5):386－392.

［7］侯世英，肖旭，张闯，等.改进型Z源逆变器［J］.电力自动化设备，2011，31(8):24－28.

［8］TANG Yu，XIE Shaojun，ZHANG Chaohua.Improved Z－source inverter with reduced Z－source capacitor voltage stress and soft－start capability［J］.IEEE Trans on Power Electron.2009，24(1):409－415.

［9］汤雨，张超华，谢少军.新型Z源逆变器［C］//2008中国电工技术学会电力电子学会第十一届学术年会论文摘要集，杭州，中国，2008:273－273.

［10］PENG F Z.Z－source inverter［J］.IEEE Trans on Industry Applications，2003，39(2):504－510.

［11］PENG F Z，SHEN Miaosen，QIAN Zhaoming.Maximum boost control of the Z－source inverter［J］.IEEE Trans Power Electron，2005，20(4):833－838.

［12］SHEN Miaosen，WANG Jin，JOSEPH A，et al.Maximum constant boost control of the Z－source inverter［C］//IEEE Industry Applications Soc Annual Meeting，Kowloon，Hong Kong，2004:142－147.

［13］ALI U S，KAMARAJ V.Double carrier pulse width modulation control of Z－source inverter［J］.Eur J Sci Res，2011，49(2):168－176.

［14］张超华，汤雨，谢少军.改进Z源逆变器的三次谐波注入控制策略［J］.电工技术学报，2009，24(11):114－126.