基于D－S证据理论的信息融合图像识别

张逵，朱大奇

(上海海事大学信息工程学院，上海 201306)

0 引言

纹理特征是物体表面共有的内在特性，是一种不依赖于颜色或亮度而反映图像中同质现象的视觉特征.纹理特征包含物体表面结构排列的重要信息以及它们与周围坏境的联系，因此在图像识别和图像分类中得到广泛应用.［1－2］

纹理分析的首要任务是提取反映图像纹理属性的数量特征.［3］纹理分析总体上可分为统计法、结构法和模型法.统计法以图像中灰度值空间分布的统计量作为纹理特征，它是目前使用最多的一种方法，如:早期的灰度共生矩阵方法［4］，近期的灰度－相位共生矩阵方法［5］、灰度－梯度共生矩阵方法［6］.对于图像识别和分类来说，单独利用灰度－相位共生矩阵法或灰度－梯度共生矩阵法提取图像纹理，对图像进行识别虽然较简单、方便，但识别准确率较低，不确定性较大，因为图像的纹理特征不仅包括灰度特性，还包括结构特性以及边缘特性.灰度－相位共生矩阵法仅包括纹理的灰度和结构特性，而灰度－梯度共生矩阵法又只包含纹理的边缘特性，显然两者都不能很好地表现纹理特征，从而难以获得准确的纹理信息识别图像.

本文将 Dempster－Shafer(D－S)证据理论［7－9］引入图像识别中，将通过灰度－相位共生矩阵法和灰度－梯度共生矩阵法得到的纹理特征参数进行D－S信息融合，能较好地包含纹理的各种信息，利用信息融合的多维信息处理优势补充单组特征参数识别的不足，与单独利用某一共生矩阵提取图像纹理特征识别图像的方法相比，图像识别的准确率提高，不确定性降低.

1 基于D－S信息融合图像识别算法概述

将D－S证据理论应用于多传感器信息融合时，通过每个传感器获得的相关参数值就是该理论中的证据，它可构成待识别目标模式的信度函数分配，表示每一个目标模式假设的可信程度，每个传感器形成一个证据组.所谓多参数信息融合就是通过D－S联合规则联合几个证据组形成一个新的综合证据组，即用D－S联合规则联合每组信度函数分配形成融合的信度函数分配，从而为目标模式的确认提供更准确的信息.

图1即为D－S信息融合技术的图像识别框图，其中纹理特征参数1(二阶距、对比度、相关性、同质性)是用灰度－相位共生矩阵得到的，纹理特征参数2(能量、小梯度优势、大梯度优势、逆差距)是用灰度－梯度共生矩阵得到的，可把这两种方法当作两个传感器处理.u0，u1，…，ue为不同类别的图像;m1(u0)，m1(u1)，…，m1(ue)是通过方法 1(灰度－相位共生矩阵)获得的待识别图像在其他类图像上的信度函数分配;m2(u0)，m2(u1)，…，m2(ue)是通过方法2(灰度－梯度共生矩阵)获得的待识别图像在其他类图像上的信度函数分配;m(u0)，m(u1)，…，m(ue)是D－S融合后待识别图像在其他类图像上的信度函数分配.

图1 D-S信息融合技术的图像识别框图

1.1 灰度-相位共生矩阵

灰度－相位共生矩阵被定义为:在角度为θ方向上，灰度级为i，相位为p的像素点离开某个固定位置关系d，到达灰度级为j，相位为q的概率，它用pd(i，j)表示.

设一幅数字图像在水平和垂直方向的尺度分别为Nx和Ny，图像的灰度级数为Nh，对于指定的像素间距离 d 和方向 θ，GL－PCM(Gray level－phase co－occurrence matrix)是一个Nh×Nh矩阵，其元素为

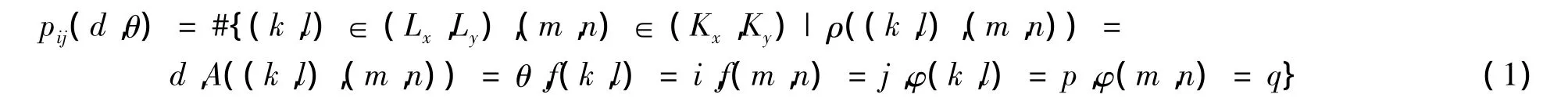
式中:#表示集中的元素数目;Lx={0，1，…，Nx－1}表示水平空域;Ly={0，1，…，Ny－1}表示垂直空域;f(k，l)和 φ(k，l)分别表示像素(k，l)的灰度级及相位;f(m，n)和 φ(m，n)表示像素(m，n)的灰度级及相位;(i，j)={0，1，…，Nh}，ρ(*)和 A(*)分别表示两像素点的距离和方向;d一般选取1;θ通常选取0°，45°，90°和 135°等4 个方向;Kx={0，1，…，Mx－1}和 Ky={0，1，…，My－1}分别表示水平频域和垂直频域.

1.2 利用灰度-相位共生矩阵提取纹理特征参数

灰度－相位共生矩阵反映的是图像灰度和相位关于方向、相邻间隔、变化幅度的综合信息.通过灰度－相位共生矩阵可以分析图像的结构及排列等.为了便于分析，先将各元素pd(i，j)除以各元素之和，由此得到归一化共生矩阵(i，j).一般用灰度－相位共生矩阵描述纹理状况不太直观，所以不直接应用得到的共生矩阵，而是在其基础上获取二次统计量.因此，通常采用下面4个最常用的统计量［10］作为特征参数提取图像的纹理特征.

1.2.1 二阶距

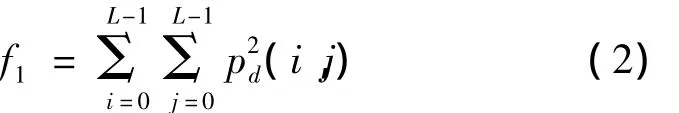
1.2.2 对比度

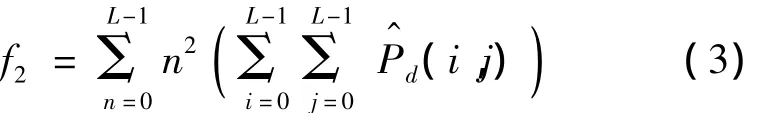
1.2.3 相关性

分别定义 μ1，μ2，为

1.2.4 同质性

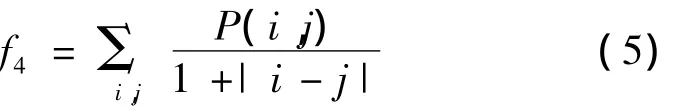
求出传感器r对目标模式ut的相关系数，记为:Cr(ut)，t∈［0，e］.这里将灰度－相位共生矩阵提取的纹理特征参数1作为传感器1(即r=1)，也即求基于灰度－相位共生矩阵法的相关系数，记为C1(ut).具体步骤如下:

(1)利用灰度－相位共生矩阵提取s+1(s=1，2，…，s为整数)张第1类图像(u1)的纹理特征参数值，即式(2)～(5)，同理可以提取第2类图像(u2)，直到第e(e为整数)类图像(ue)(均为s张)的纹理特征参数值;

(2)由于共生矩阵有0°，45°，90°和 135°等 4 个方向，将前s张u1的纹理特征参数在0°方向上组成矩阵a1;同理，前s张u2的纹理特征参数可以组成矩阵a2，前s张ue的纹理特征参数可以组成矩阵ae;

(3)将第s+1张u1作为待识别图像，同样将其0°方向上的纹理特征参数作为一特征向量x1;

(4)分别求 x1与 a1，a2，…，ae之间的欧氏距离，记为 d1(u1)，d1(u2)，…，d1(ue);同理，45°，90°和135°方向上的欧氏距离也可以求出，于是可以得到一个4×e的距离值矩阵b，接着对矩阵b按列求平均，得到平均距离值d^1(u1)，d^

1(u2)，…，d^

1(ue);

(5)对平均距离值进行归一化，除以它们的和，得到各距离值的概率p1(u1)，p1(u2)，…，p1(ue);

(6)为了与信度函数值相吻合，用1减去各个距离值的概率，然后各值除以总图像类数e进行归一化，得到归一化的距离值概率，也即为所求的相关系数C1(ut).

1.3 灰度-梯度共生矩阵

定义灰度－梯度共生矩阵的元素H(i，j)为在归一化的梯度图像 G(m，n)和归一化的灰度图像F(m，n)中共同具有灰度为i和梯度为j的总像点数，以图像的总像点数归一化后得到概率p(i，j).例如H(4，6)=18，即图像内像点灰度为4、梯度为6的总像点数为18.

(1)梯度、灰度归一化处理.采用3×3窗口的Sobel算子计算各像点的梯度值:

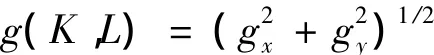
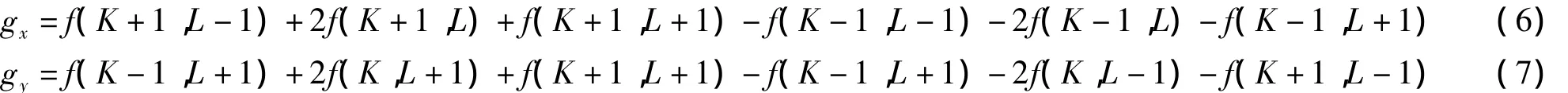
式中:K=1，2，…，M，M 为图像的行数;L=1，2，…，

N，N为图像的列数;g(K，L)为(K，L)像点的梯度值.

①梯度归一化变换:

式中:gM是图像的最大梯度值;INT是取整运算符;Ng是归一化的最大梯度值.

②灰度归一化变换:

式中:NH是归一化的最大灰度值;fM是原图像的最大灰度值.

(2)统计灰度－梯度共生矩阵.在归一化的灰度图像F(m，n)和归一化的梯度图像G(m，n)中，统计同时使 F(m，n)=i和 G(m，n)=j的像点对数(即为灰度－梯度共生矩阵C的(i，j)元素的值Cij)在灰度值为i且梯度值j处的共生矩阵概率

1.4 利用灰度-梯度共生矩阵提取纹理特征参数

虽然灰度－梯度共生矩阵在许多方面包含纹理的各种特性，但它并不是直接作为纹理分割或分类的特征，一般是在其基础上产生一些统计量，并以此作为纹理特征.本文利用如下统计量作为特征参数［6］.

1.4.1 能量

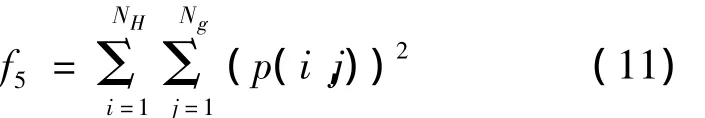
1.4.2 小梯度优势

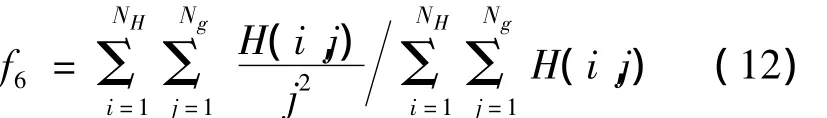
1.4.3 大梯度优势

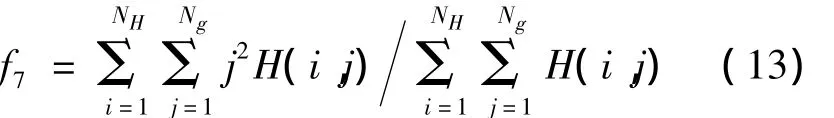
1.4.4 逆差距

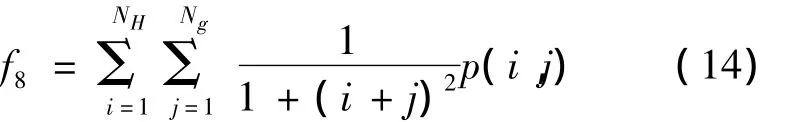
于是，可以求出基于灰度－梯度共生矩阵法的相关系数，记为C2(ut).具体步骤如下:

(1)利用灰度－梯度共生矩阵提取s+1(s=1，2，…，s为整数)张第1类图像(u1)的纹理特征参数值即式(11)～(14);同理，可以提取第2类图像(u2)，直到第e(e为整数)类图像(ue)(均为s张)的纹理特征参数值;

(2)将前s张u1的纹理特征参数组成矩阵b1，同理前s张u2的纹理特征参数可以组成矩阵b2，前s张ue的纹理特征参数可以组成矩阵be;

(3)将第s+1张u1作为待识别图像，同样将其纹理特征参数作为一特征向量x2;

(4)分别求y与b1，b2，…，be之间的欧氏距离，记为 d2(u1)，d2(u2)，…，d2(ue);

(5)对距离值进行归一化，除以它们的和，得到各距离值的概率p2(u1)，p2(u2)，…，p2(ue);

(6)为了与信度函数值相吻合，用1减去各距离值的概率，然后各值除以总图像类数e进行归一化，得到归一化的距离值概率，也即为所求的相关系数C2(ut).

2 信度函数分配及信度函数

将证据理论的论域称为识别框架，记为Θ，包括有限个基本命题，记为{u0，u1，…，ue}，对应概率论中的基本事件，称为基元，在目标识别中对应基本的待识别图像，Θ中的事件是互斥的.

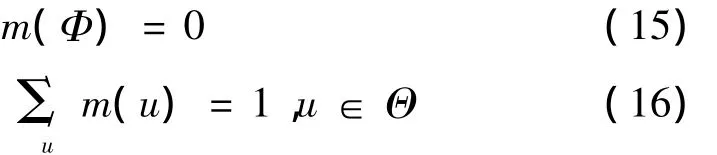
定义1 设Θ为识别框架.如果集函数m:2Θ→［0，1］(2Θ为 Θ 的幂集)满足称m为框架Θ上的信度函数分配，此处Φ为空集，对u∈Θ，称m(u)为u的信度函数值，当m(u)≠0时，称u为信度函数分配上的焦元，u的信度函数值反映对u本身的信度大小，即确切地分配到u上的信度函数值.

2.1 信度函数的获取

信度函数分配表示人对目标模式假设的可信程度的一种推理，根据文献［7］，信度函数分配的公式为

式中:Cr(ut)是传感器r对目标模式ut的相关系数，表示根据某传感器测量值评估被测对象隶属于某一目标类型的程度，例如C1(u1)表示通过方法1(灰度－相位共生矩阵)测量值评估被测对象隶属于u1类型的程度;N是传感器总数;Wr是传感器r的环境加权因数，其值域为［0，1］;Nc为目标模式数目;αr是传感器r的最大相关系数;βr是传感器r的相关分配值;Rr是传感器r的可靠性系数.于是传感器r对目标模式ui的信度函数

式中:Q为修正因数，它的引入实际上是把空集所丢弃的信度分配按比例地补到非空集上;传感器r的不确定性θ的信度函数为

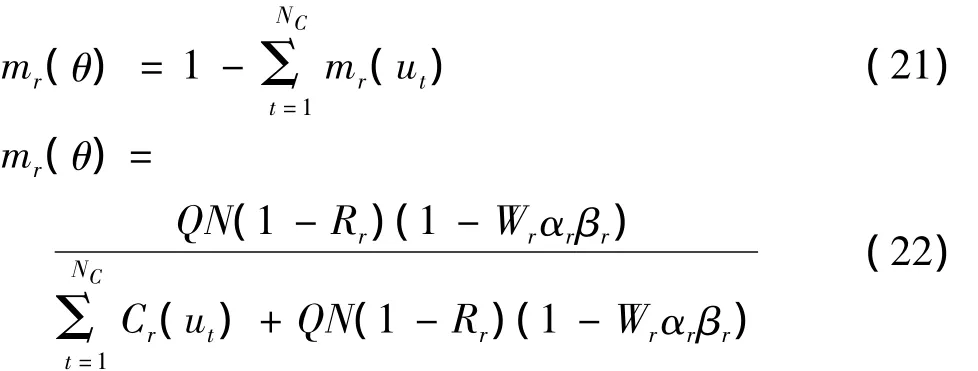
2.2 D-S融合原则

(当A=Φ时，m(A)=0)

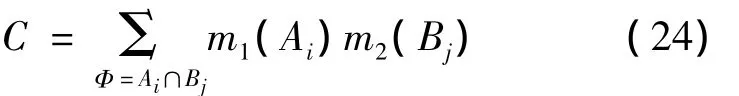
式(24)中的目标模式Ai和Bj代表在Θ中不可同时存在，即相互排斥，此处Φ表示空集;式(23)中A指的是目标模式Ai和Bj同为某一种目标，A的信度函数值m(A)为互不排斥的Ai和Bj的所有信度函数乘积之和.在判断识别中焦元 A1，A2，…，Ae和B1，B2，…，Be即为前面所指的不同类别图像 u0，u1，…，ue，而m(A)是指融合后待识别图像分配到其他类图像上的信度函数值.

2.3 目标模式判定规则

在文献［7］～［9］中判定规则的基础上，根据具体的实验数据选取阈值，对目标模式的分类决策采用基于规则的方法，其基本原则有:

(1)判定的目标类型应具有最大的信度函数值，且要大于某一阈值(下面实验中取0.4).

(2)判定的目标类型与其他类型的信度函数值之差要大于某个门限(下面实验中取0.2).

(3)不确定信度函数值必须小于某个门限(下面实验中取0.1).

3 图像融合识别实验及结果分析

图2 实验所用图像

图2为实验所用的3类图片，它们来自网上图像标本库，图2(a)为4张大理石u1，其中第4张作为待识别图像;图2(b)为3张花u2;图2(c)为3张某草细胞u3.已知现要识别的是一幅大理石图片，具体识别时，按照前面求C1(ut)和C2(ut)的步骤先分别求出灰度－相位共生矩阵和灰度－梯度共生矩阵在各个待识别图像上的相关系数值(见表1)，然后再求出他们的信度函数值，最后利用D－S证据理论将这两种方法获得的两组信度函数值进行融合，得到一组新的信度函数值，与单方法的信度函数值相比较并分析结果.

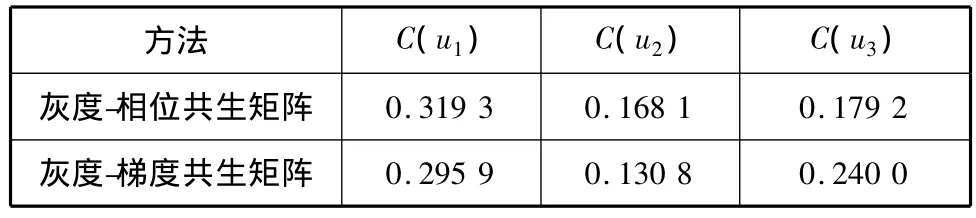
表1 灰度-相位共生矩阵和灰度-梯度共生矩阵的相关系数

3.1 信度函数的计算

由式(20)和(21)可计算信度函数mr(ut)和不确定度mr(θ).此处，特征参数数目N=2，待识别的图像数目Nc=3，依据文献［7］～［9］以及一定的主观经验，一般选取权因数W1=W2=0.5，修正因数Q=0.20，由式(17)～(19)计算得到:

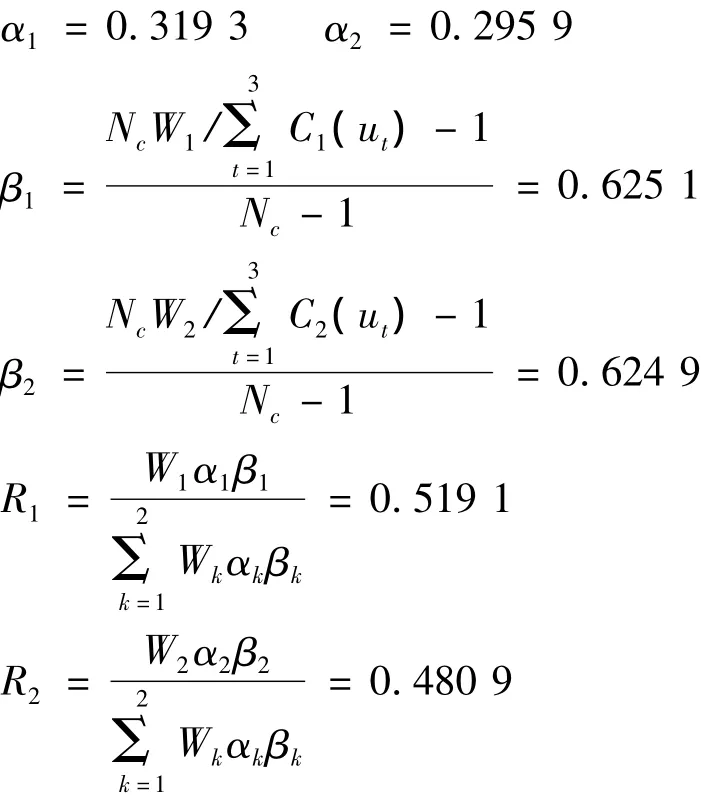
于是大理石u0的信度函数

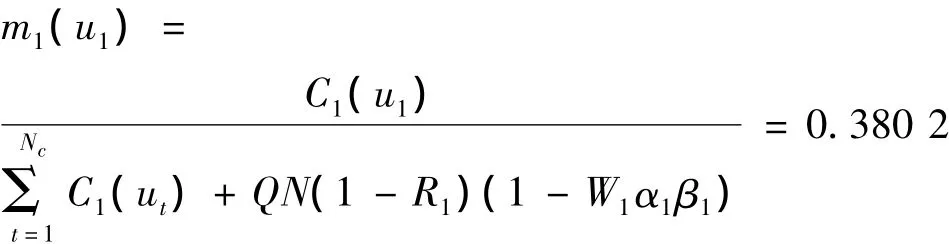
同样可计算其他信度函数值及不确定值，见表2.

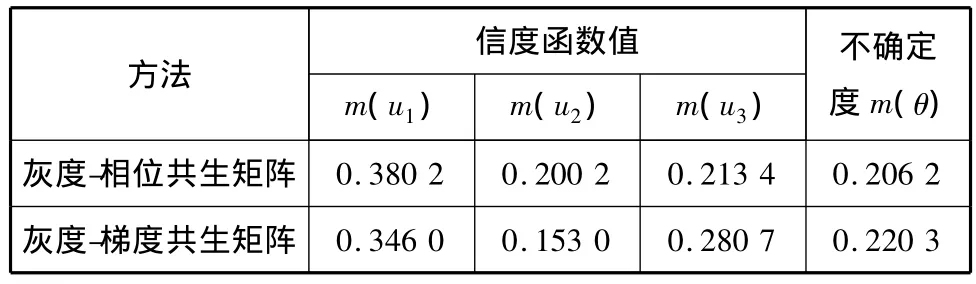
表2 两矩阵的信度函数值

由式(23)和(24)可进行融合运算，Φ表示空集，由此可计算融合信度函数值m(ui).

由式(24)可得

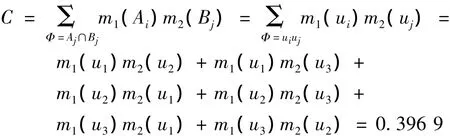
再由式(23)可得出融合后分配到大理石(u1)上的信度函数值

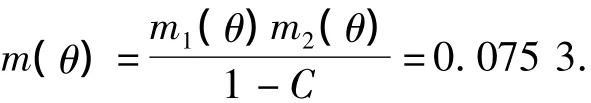
对另外两幅图像，可采用同样方法进行融合计算.

3.2 融合识别结果

表3为基于灰度－相位共生矩阵法和灰度－梯度共生矩阵法获得的待识别图像在其他类图像上的信度函数分配表及经过D－S数据融合后的图像识别结果.从表3可以明显看出，融合后的信度函数值与两矩阵的信度函数值相比，实际图像的信度函数值增加，其他类型的信度函数值相对减少，特别是融合结果中，不确定度m(θ)大为减少，从而降低识别的不确定性.因此，对单独利用某一共生矩阵提取图像纹理特征识别图像的方法，无法准确判断图像类型，经融合信息处理后，其实际类别图像(大理石)的信度函数值大为提高，能准确识别出是大理石，这与实际情况相吻合.因此，基于D－S证据理论的数据融合能有效提高识别的准确率.

表3 两矩阵单独识别和D-S融合后识别结果比较

4 结束语

阐述基于D－S证据理论和模糊集合论的数据融合算法，并首次将其应用于图像识别之中.提出一种基于D－S信息融合的图像识别算法，实验结果表明，数据融合能提高图像识别的准确率、较好地解决不确定性问题.另外，虽然本文只是对几幅图片进行融合识别，但对于多类多幅待识别图像，只要能较准确地得到各幅图像的信度函数，就能准确地识别出图像类别.本文将D－S信息融合算法应用到机器人侧扫声呐及前视声呐图像识别中，也证实此方法的有效性.因此，此融合识别方法完全能够应用于实际图像分类中.

［1］刘丽，匡纲要.图像纹理特征提取方法综述［J］.中国图像图形学报A，2009，14(4):622－635.

［2］TAN X Y，TRIGGS B.Enhanced local texture feature sets for face recognition under difficult lighting conditions［J］.IEEE Trans Image Processing，2010，19(6):1635－1650.

［3］王琨，齐会来，杨波，等.基于纹理的图像检索算法［J］.空军工程大学学报:自然科学版，2008，9(3):54－57.

［4］刘昶，王玲.基于灰度共生矩阵的鞣制皮革图像分类［J］.图像处理，2008，125(9):301－303.

［5］WANG Z H，HUANG X D.Principle of phase measurement and its application based on all－phase spectral analysis［J］.J Data Acquisition ＆ Processing，2009，24(6):777－782.

［6］白雪冰，邹丽晖.基于灰度－梯度相位共生矩阵的木材表面缺陷分割算法［J］.森林工程，2007，23(2):16－18.

［7］朱大奇，于盛林.基于D－S证据理论的数据融合算法及其在电路故障诊断中的应用［J］.电子学报，2002，30(2):221－223.

［8］ZHU D Q，GU W.Sensor fusion for integrated circuit fault diagnosis using a belief function model［J］.Int J Distribute Sensor Networks，2008，6(4):247－261.

［9］朱大奇，于盛林.故障诊断的D－S信息融合算法比较分析［J］.控制理论与应用，2004，21(4):559－663.

［10］杨帆.数字图像处理与分析［M］.北京:北京航空航天大学出版社，2007:277－281.