柱状结构条纹列板对尾涡形态变化的影响机理

郝志永，余恒旭，宓为建

(上海海事大学物流工程学院，上海 201306)

0 引言

目前，海洋立管涡激振动研究主要采用两种方法:一种是依赖于实验数据的经验型预测;另一种是通过数值方法进行分析和预测.当流体流经海洋立管结构时，会在其表面产生周期性旋涡脱落，使结构表面所受的水流局部压力发生改变.如果结构是柔性的或者安装呈柔性，脱落的旋涡之间的相互作用会导致结构挠度上升.这种情况会激发持续振动，振动频率大致等同于旋涡脱落的频率.如果旋涡脱落的频率接近结构的固有频率，就会产生共振现象，导致结构疲劳及失效.因此，岸边港口机械在风的作用下或海洋工程结构(如浮筒式采油平台或海洋立管)在涡流的作用下可能遭受重大损失.［1－2］

李晓猛等［1］探讨港口岸边起重机结构中圆截面杆件风振的机理，指出这类杆件的风振主要是涡激振动，并对引起港口岸边起重机结构中常用规格的圆截面杆件涡激振动的风速以及轴力、杆件长度、两端的约束形式对共振风速的影响作定量计算.郑苏等［2］提出利用抗扰条肋抑制此类风振的方法，并通过试验模拟港口岸边起重机圆截面杆件在横向风作用下的振动，在抑制涡激振动方面取得一定的效果.

目前，已有很多流体控制技术［1－4］用于涡激振动的抑制，其中包括被动和主动控制.利用螺旋列板抑制涡激振动的方法已比较普遍，对此前人做了大量的研究［5－13］，然而螺旋列板对涡激振动的抑制机理仍存在很多未知和疑问.因此，对绕有螺旋列板的立管尾流涡结构进行基础性实验研究，仍具有非常重要的意义，这也有助于建立更准确的数学预测模型，以进行港口机械或海洋立管涡激振动受力预测及结构疲劳分析.

杨加栋等［10］阐述螺旋条纹列板参数(如基本尺寸、包覆比率、海洋生物等)对涡激振动抑制效率的影响，建议列板的设计应依据载荷工况、立管固有特性及涡激振动疲劳分析确定螺头数、节距和列板高等参数.CONSTANTINIDES等［11］采用2种湍流模型进行计算，并将计算结果与试验结果进行对比，表明计算流体力学(Computational Fluid Dynamics，CFD)可以在一定程度上预测抑制涡激振动的效果，揭示螺旋条纹列板抑制机理.盛磊祥等［12］利用CFD求解螺旋列板的三维流场控制方程，计算出钝体隔水管的三维扰流流场，并对流场参数(升力系数、曳力系数、涡量)进行对比分析，结果表明螺旋列板能够减小横向升力，但同时会导致流向曳力的明显增加.苑健康等［13］进一步对有螺旋侧板的系统曳力系数进行研究，发现在一定范围内，随着雷诺数的增加螺旋列板的曳力系数发生较大变化，但均在0.8～2.2之间，与实际应用情况相符，螺旋列板的使用得到充分肯定.

关于螺旋列板参数选择，国内外学者也做了大量工作.王兴刚等［14］的试验表明螺圈数的增加会显著影响垂荡方向的水动力特性和二阶平均波浪力，主要比较对象为 1螺圈、2螺圈和 3螺圈.MARINTEK实验室的结果［15］表明:与3螺圈相比，4螺圈在抑制涡激振动的效率方面效果变化不大，但螺圈数的增加会带来曳力系数的升高及立管的疲劳损坏.由此，本文选用3螺头的螺旋条纹组合.实验室还给出节距定义的范围，即节距在5.0D～17.5D(D为立管直径)时均可产生较好的抑制效果.周阳［16］的研究表明:螺旋列板可以很好地抑制立管的横向振动，但会带来顺流方向上振幅的增加，甚至超过横向振幅.通过对比各节距，认为螺旋列板的节距大小对横向振型没有影响，但节距的增加可以在流向上激发二次振型并随之放大.认为节距为3.5D～6.0D较合适.螺旋列板的高度对抑制涡激振动效率非常敏感［17］，随着高度的增加，抑制效率明显增加.当高度大于0.1D时，抑制效果可高达80%.王增波等［18］在选取不同螺纹高度的情况下进行曳力系数和升力系数的参数对比发现:螺纹越高，螺旋列板受到的作用越大，对旋涡泄放的影响越大，且影响旋涡泄放的频率;升力的变化不是单纯的正弦变化，板后的旋涡长度和传播距离随之发生改变，同时也改变流场的流速和压力;曳力在一个周期内产生两次波动，从侧面证明对涡激振动的抑制作用，但实验基于二维流场，未考虑三维流场条件下流体之间的相互作用以及立管整体作用.

娄敏等［19］研究波浪作用下海洋立管数值模拟，参考某一工程实例中的立管参数，按照相似理论将其缩放到试验水槽，结果发现软件计算的振动形态基本吻合，但振幅存在偏差，因为实体立管会存在应力集中现象，与CFD软件ANSYS的理想边界条件差别较大，试验结果比数值模拟的结果大，实际运用更应考虑偏差系数问题.张蕙等［20］对螺旋列板消涡装置进行试验研究，为螺旋列板在海洋工程上的实际运用给出很好的指导说明.

由上所述，很多学者对螺旋条纹列板涡激振动问题进行研究，然而利用粒子图像测速(Particle Image Velocimetry，PIV)系统对光滑圆柱及螺旋条纹圆柱的尾流流场进行测量的文献较少.因此，本文利用PIV对比研究不同螺纹高度的螺旋列板圆柱和光滑圆柱尾流流场，探讨螺旋列板对圆柱绕流涡结构及旋涡脱落模式的影响，同时进行CFD计算比较分析，以进一步揭示螺旋条纹列板抑制涡激振动的机理.

1 试验条件

1.1 试验水槽

开环试验水槽长6 m，观测截面0.3 m×0.4 m(宽×高)，分别放置两个钢材料管(具有螺旋条纹圆柱及光滑圆柱)，水平固定在测试区的中部平面.为了最大限度降低来流湍流度，水槽配有消涡段、穿孔钢板和蜂窝式收缩屏，最终测得来流的湍流度为2%.

1.2 PIV

Lavision PIV用于测量流场，不仅要足够大的观测区域，还需兼顾流场分辨率.本试验选择的观察区域为125 mm×95 mm.激光系统为Nd:YAG激光(能量为120 MJ/脉冲，持续时间5 ns)，相机为12位CCD相机，分辨率为1.6 K×1.2 K，帧速为15 Hz.图像处理的过程包括两个方面，起始网格为64×64像素，逐渐降到32×32，像素重叠50%.因此，目前的图像分辨率为1.25 mm×1.25 mm.一般地，瞬时流场为1 050帧时才能得到一个合理的统计意义上的收敛流场.其他参数包括示踪粒子大小(约3个像素)及粒子密度(约10～30个/mm2)，均为经过反复试验得到的优化值.因此，选择空心玻璃珠直径为10～15 μm，作为示踪粒子播种在流体里，密度为1.05×103～1.15×103kg/m3.双脉冲之间的延时暂设置为1 000，2 000，3 000 μs，分别对应不同试验流速0.2，0.4，0.6 m/s.

1.3 光滑圆柱及螺旋条纹列板圆柱

图1 螺旋条纹列板圆柱物理模型

光滑圆柱直径D=12 mm，长度 300 mm(与水槽的宽度相等)，纵横比为25.由图1可见，3螺头螺旋条纹列板圆柱有3

条薄板并呈螺旋状缠绕，其中列板节距P=25D，螺旋条纹高度分别为h=0.1D和0.2D.螺旋条纹截面参数:3条螺旋条纹在截面上平均分布，夹角为120°;螺旋条纹宽度为2 mm(见图2).基于光滑圆柱的雷诺数(Re=UD/v，U为水流速度，v为水的动力黏度系数)分别为2 400，4 800和7 200.为了观察沿翼展方向上的旋涡脱落，运用PIV测量不同攻角α下的瞬时尾流流场.

为了能够更好地理解螺旋条纹列板对涡激振动的抑制机理，进行CFD数值模拟.数值模型与物理试验模型的几何尺寸相同(1∶1).图3给出数值模拟计算中3螺头螺旋列板的模型及其表面网格.CFD软件中ANSYS CFX的数值方法为有限体积法，可以针对本文所采用的不规则网格展开计算.采用的湍流模型为SST模型(剪切压力传输模型).

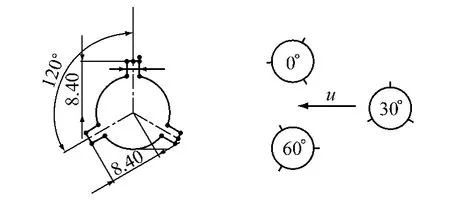
图2 螺旋条纹列板圆柱体横截面(左)及来流攻角方向(右)，α =0°，30°，60°

图3 螺旋条纹列板圆柱体数值模型及其表面网格

2 结果与讨论

2.1 平均速度矢量图

图4为PIV测得的平均速度矢量(U，V)图，U=0.6 m/s，α =30°，图中螺纹高度h分别为0.1D(1.2 mm)和0.2D(2.4 mm).黑色流线也绘制在图中，以显示流体形态.对于光滑圆柱尾流，两个对称的回流区域在圆柱两边被剪切层分离为两个区域:逆时针回流区域位于上部，向下游延伸直到闭合循环;顺时针回流区则位于圆柱体下游相对较低的位置.对h=1.2 mm(图4(b))的列板，上下两个回流区域都清晰可见.可以观察到，相对于光滑圆柱体，回流区域的顺流长度增加:光滑圆柱体的平均附着点发生在大约－1.8D处;有列板存在时(h=1.2 mm)平均附着点发生在 －2.8D处.当 h=2.4 mm时(图4(c))，矢量场显然不是沿y=0的对称形态.中心部分上层的逆时针回流区在－1.8D左右，而顺时针回流区在－2.5D左右.对h=2.4 mm的列板，该回流区域的流向长度增加，平均附着点大概在－4.5D.由此可以看出，与图4(a)相比，图4(b)和4(c)回流区纵向及横向长度均变大，平均附着点向柱体靠近，并且随着列板高度的增加出现回流区上下不对称情况.这种现象的发生是因为螺旋列板的存在使圆柱的有效直径增加、边界层条件发生改变，进而影响剪切层从圆柱壁面的分离和脱落.剪切层脱落模式的改变亦可在下述瞬时速度矢量图及瞬时涡量图中观察到.剪切层脱落模式的改变会干扰尾流域附近的回流区、旋涡脱落模式及压力场，使尾流域附近有序流场和压力场受到干扰直至非对称，直接影响下游旋涡脱落，从而在一定程度上抑制涡激振动.

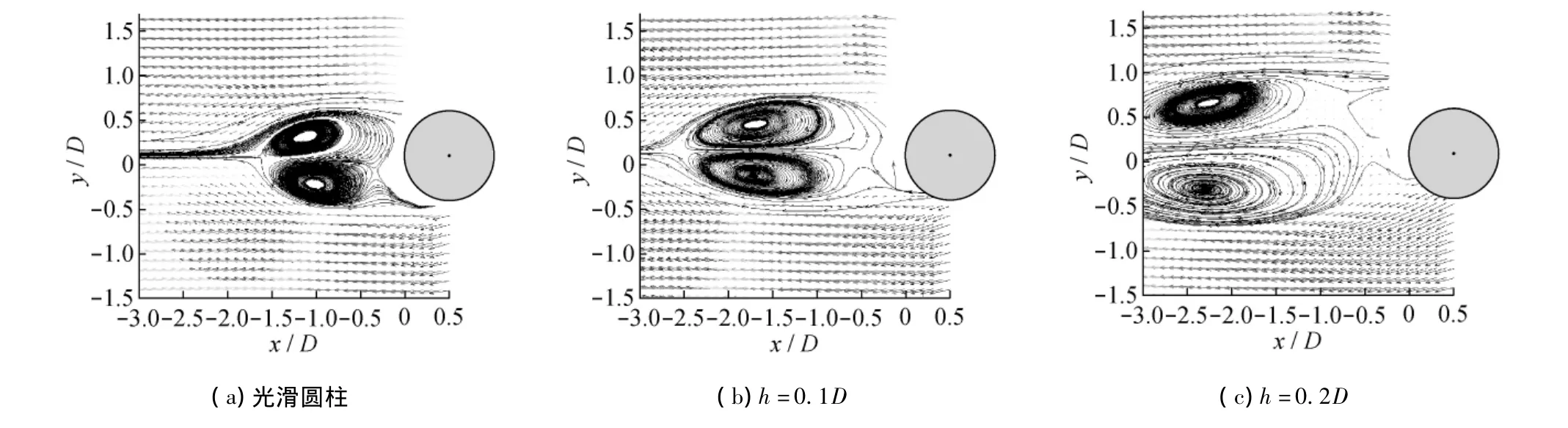
图4 平均速度矢量(U，V)图 (U=0.6 m/s，α=30°)

2.2 标准雷诺应力等高线

图5是标准雷诺应力等高线图(U=0.6 m/s，α=30°)，实线表示正等高值，虚线为负等高值.

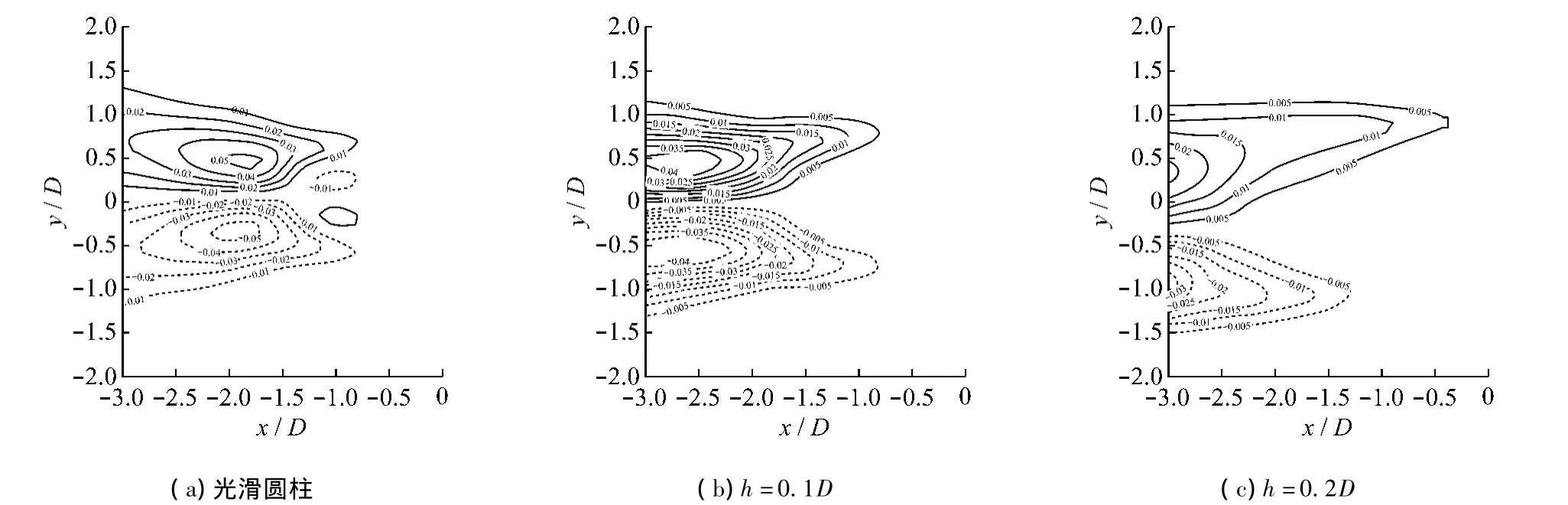
图5 标准雷诺应力等高图(－U2V2/U2g，U=0.6 m/s，α=30°)

图5(a)，5(b)和5(c)分别代表光滑圆柱体、h=0.1D(1.2 mm)和h=0.2D(2.4 mm)的螺旋条纹列板.对于光滑圆柱体和h=1.2 mm的螺旋列板，标准雷诺数的分布表现出中心对称.但是对于光滑圆柱体，有两个额外的小尺度峰值(0.01)出现于圆柱尾流近区.雷诺应力的最大峰值区向远区迁移:光滑圆柱雷诺应力峰值出现在约－1.8D处;h=1.2 mm的螺旋列板峰值出现在 －2.8D;而 h=2.4 mm的螺旋列板，峰值移动至－3D处，且雷诺应力呈非均匀、非对称形态.由图5也可看出，h=2.4 mm的螺旋条纹列板相对于光滑圆柱体，标准雷诺应力从0.05下降到0.03.

2.3 瞬时涡结构图

通过观察平均速度矢量和雷诺应力分布可以观察到螺旋条纹列板对瞬时流场及旋涡脱落形态的影响.图6和7显示瞬时速度矢量(U，V)图和沿翼展方向涡量图(设参考速度为0.5Ue).

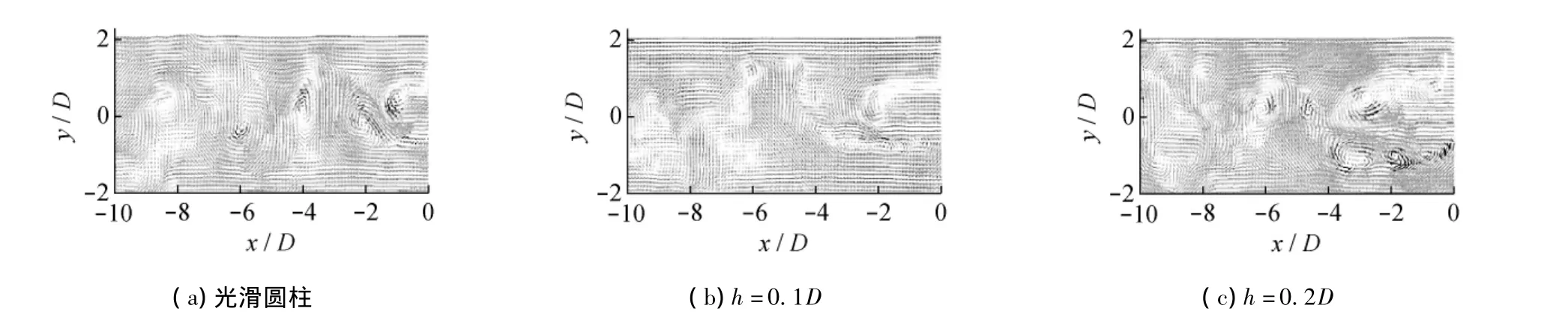
图6 瞬时速度矢量(U，V)图 (U=0.6 m/s，α=30°)

在图6(a)和7(b)中，上下两个剪切层相互卷起并互相渗透，带动边界层规律性的压力波动，进而在尾流区形成周期性的旋涡脱落.旋涡集中区域正负旋涡交替出现，并围绕对称中心上下振荡(x/D=－2和－6为负旋涡，x/D=0.5，－4和 －8.2为正旋涡).对螺旋条纹情况下的图6(b)，6(c)，7(b)和7(c)来说，尾流旋涡清晰可见，然而上下两个剪切层的自发性耦合作用大大降低，大尺度的旋涡耗散成一个个断续的小尺度旋涡，无法形成正负旋涡的周期性交替，也就无法观测到周期性的旋涡脱落.同样，螺旋条纹列板情况下由于大涡结构耗散成小涡结构，剪切层在下游x/D=－4处停止卷起，剪切层耦合作用消失.由此可以推测，螺旋条纹圆柱尾流旋涡脱落频率将大大降低，甚至消失.

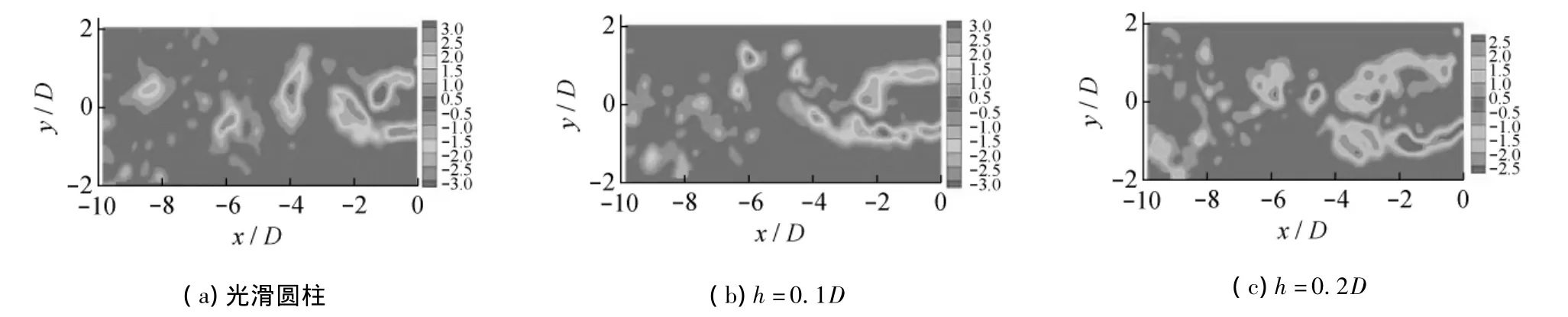
图7 瞬时涡量图(PIV结果，ωzD/Ue，U=0.6 m/s，α=30°

图8为3种不同攻角下的条纹列板尾流场瞬时涡量图，攻角 α 分别为 0°，30°和60°.

图8 3种不同攻角下的瞬时涡量图 (ωzD/Ue，U=0.6 m/s，ω =0°，30°，60°)

由图8可见，在不同螺旋条纹列板高度下，与α=30°和60°时相比，α=0°时条纹列板对尾流流场的扰动更为显著，原因在于α=0°时条纹列板圆柱有效干扰直径最大，列板沿来流方向对称(见图2).从涡量图上看，α=60°时条纹列板对旋涡的破坏能力似乎较弱，前端列板平行于来流方向，会减弱前端列板对流场的扰动，只有靠近后端的2条关于来流方向对称的列板对旋涡起到破坏作用，因而3螺头螺旋列板对涡流结构的影响整体下降.

为进一步探讨螺旋条纹列板对圆柱尾流旋涡结构的破坏，进行CFD数值仿真.CFD所得瞬时涡量图(图9)表明螺旋条纹列板的存在会破坏圆柱绕流涡量场，从而达到抑制涡激振动的效果，且螺旋条纹列板螺纹高度越高，对旋涡结构破坏效果越强.这与运用PIV所观察到的现象吻合.图7和8均为瞬时涡量图，由于试验及仿真时刻选择的不确定性，两图瞬时涡量场在具体细节上不具有可比性.然而，通过比较仍可以看出，图7和9中，无量纲化后的涡量强度幅度(ωzD/Ue)及旋涡脱落形态上依然具有很强的可比性(幅值均在－3～3之间).从图7(a)和9(a)都可以观察到有规律的旋涡脱落，而随着螺纹高度的增加(图7(b)，7(c)及9(b)，9(c))，剪切层从圆柱壁面的分离和旋涡脱落受到螺旋条纹的扰动越来越大，尾流上下剪切层及旋涡(顺时针、逆时针)相互作用区间变大、周期变长，涡激振动抑制效果也越来越明显.

图9 瞬时涡量图(CFD仿真，ωzD/Ue，U=0.6 m/s，α=30°)

3 结束语

在U=0.6 m/s，α=30°的条件下通过PIV展开对螺旋列板涡激振动抑制效果的试验研究和分析，并结合CFD数值仿真探讨螺旋列板的涡激振动抑制机理.结果显示螺旋条纹列板明显影响边界层和剪切层的形成及尾流旋涡脱落形态，破坏规律性的正负旋涡交替，进而抑制周期性的旋涡脱落，从而达到抑制涡激振动的效果.在本文实验条件下，h=0.2D时螺纹列板对涡激振动抑制效果好于h=0.1D时的抑制效果，对尾流的干扰度也更大.瞬时速度矢量和沿翼展方向瞬时涡量等高图表明:螺旋条纹列板情况下，剪切层在下游距离圆柱体x/D=4时停止卷起，并逐渐由大涡结构耗散成小涡结构.对比3种不同攻角下的瞬时涡量图，在不同螺旋条纹列板高度下，α=0°时列板对尾流流场的扰动最为明显，而α=60°时对旋涡破坏效果最小.CFD所得瞬时涡量图表明螺旋条纹列板的存在会破坏圆柱绕流涡量场，从而达到抑制涡激振动的效果，且螺纹高度越高，螺旋条纹列板对旋涡结构的破坏效果越强.这与PIV试验所观察到的现象吻合.

［1］李晓猛，郑苏.引起岸边起重机结构中圆截面杆涡激振动的风速［J］.上海海事大学学报，2005，26(2):21－26.

［2］郑苏，钞素莉，唐军领.圆截面杆件涡激振动控制结构实验［J］.上海海事大学学报，2006，27(4):14－17.

［3］BEARMAN P，BRANKOVIC M.Experimental studies of passive control of vortex－induced vibration［J］.Eur J Mech B/Fluids，2004，23(1):9－15.

［4］黄维平，曹静，张恩勇，等.大柔性圆柱体两自由度涡激振动试验研究［J］.力学学报，2011，43(2):437－440.

［5］DONG S，TRIANTAFYLLOU G S，KARNIADAKIS G E.Elimination of vortex streets in bluff－body flows［J］.Physical Review Letters，2008，100(20):1547－1549.

［6］KORKISCHKO I，MENEGHINI J，GIORIA S，et al.An experimental investigation of the flow around staked cylinders［C］//Proc 26th Int Conf on Offshore Mech＆ Arctic Eng.San Diego，California，USA.2007:29057.

［7］SUMER B M，FREDSOE J.Hydrodynamics around cylindrical structures［M］.Singapore:World Sci Publishing，2006.

［8］THIAGARAJAN KP，CONSTANTINIDES Y，FINN L.CFD analysis of vortex－induced motions of bare and straked cylinders in currents［C］//Proc 24th Int Conf on Offshore Mech＆ Arctic Eng.Halkidiki，Greece.2005:67263.

［9］ZDRAVKOVICH M M.Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding［J］.J Wind Eng＆ Ind Aerodynamics，1981，7(2):455－472.

［10］杨加栋，张晓灵，杜宝银，等.螺旋列板—深水立管涡激振动抑制装置［J］.海洋技术，2010，29(4):88－92.

［11］CONSTANTINIDES Y，OAKLEY O H.Numerical predictions of bare and straked cylinder VIV［C］//Proc 25th Int Conf on Offshore Mech＆ Arctic Eng.Hamburg，Germany.2006:92334.

［12］盛磊祥，陈国明.螺旋列板绕流流场CFD分析［J］.中国造船，2010，51(1):79－83.

［13］苑健康，黄维平.二维立管Helical Strakes绕流场的ANSYS－CFD分析［J］.船海工程，2010，39(4):151－155.

［14］王兴刚，孙昭晨，梁书秀，等.水深和螺旋板对 Classic Spar水动力特性的影响［J］.中国海洋平台，2011，26(1):23－30.

［15］BAARHOLM R，LIE H.Systematic parametric investigation of the efficiency of helical strakes［C］//Deep Offshore Technol Conf，2005.

［16］周阳.螺旋侧板涡激振动控制实验研究［C］//第十五届中国海洋(岸)工程学术讨论会论文集.南京，2011:253－257.

［17］鞠少栋，陈国明，盛磊祥，等.基于CFD的深水隔水管螺旋列板几何参数优选［J］.中国石油大学学报，2010，34(2):111－113.

［18］王增波，黄维平，苑健康.立管扰流装置Helical Strakes的数值模拟分析［J］.石油化工高等学校学报，2011，24(4):80－83.

［19］娄敏，董文乙，郭海燕.波浪作用下海洋立管试验研究及ANSYS数值模拟［J］.中国造船，2010，51(1):73－77.

［20］张蕙，杨建民，肖龙飞，等.均匀流中深水系泊Truss Spar平台涡激运动试验研究［J］.海洋工程，2011，29(4):15－20.