一种改进的关联规则挖掘算法

白雪峰

摘要：针对Apriori算法存在的缺陷，提出一种改进的关联规则算法。该算法对数据库中的项采用二进制编码，且只需扫描一次事物数据库就能找出所有的频繁项集，减少了扫描数据库的次数和计算成本，从而大大提高了算法的执行效率。

关键词：关联规则；Apriori算法；频繁项集；数据挖掘；数据库

中图分类号：TP311.13文献标识码：A文章编号：1009-3044(2012)05-1015-04

An Improved Algorithm for Mining Association Rules

BAI Xue-feng

(Chongqing Three Gorges Medical College, Chongqing 404120, China)

Abstract: According to the inefficiency problems about the Apriori algorithm, this thesis proposes a new improved algorithm of association rules. This algorithm uses the binary code to the database item. This algorithm is able to discover all the frequent item sets only by searching the database once. Because this algorithm reduces the number of scanning the database and computational cost, so it has higher efficiency.

Key words: association rule; apriori algorithm; frequent item set; date mining; database

关联规则挖掘是研究人员于1993年研究市场购物篮问题时提出的[1]，它是用来从大量的数据中挖掘出数据项间隐藏的相互关联的有用知识，应用极其广泛，在数据挖掘中具有重要的地位。

针对关联规则的经典算法—Apriori算法存在的不足，本文提出了一种新的关联规则挖掘算法—GApriori算法，该算法对数据库中的项采用二进制编码，提高了算法的执行速度，节省了大量的时间。同时，该算法只需对数据库进行一次扫描就能找出所有的频繁项集，而连接前剪枝有效的减少了挖掘过程中需要进行连接的项集数目，因而对算法效率有了很大提高。

1关联规则挖掘

先介绍关联规则的几个基本概念，具体描述如下[2]：

定义1：假设关联规则挖掘的事务数据集记为D，其中，D= {t1,t2,…,tk,…,tn}，tk={i1,i2,…,im,…ip}，那么tk（k=1，2，…，n）称为事务(Transaction)，im（m=1，2，…，p）称为项目（Item）。

定义2：假设I={i1,i2,…,im }是由D中所有项目组成的集合，则I的每一个子集X就称为D的项目集（Itemset）。假设X、Y都是项目集，且X?Y=?，则蕴含式X?Y称为关联规则。

定义3：对于关联规则X?Y，如果数据集D中拥有项目集X?Y的个数为σ，交易数据集D的事务数为||D，那么，关联规则X?Y的支持度就是σ与||D之比。

定义4：如果项目集X的支持度大于等于事先设定的最小支持度minsupport，那么就称X为频繁项目集。

关联规则的挖掘过程是先查找符合既定条件的频繁项集，然后利用频繁项集生成关联规则。通过对数据库使用关联规则挖掘，可以得到一些潜在有用的挖掘结果。将这些结果同事先设定的最小支持度minsupport和最小置信度minconfidence进行比较，如果其值不小于事先设定的值，那么就是有趣的规则。

Apriori算法是通过对数据库进行反复逐层搜索，来得到频繁项集。首先，对数据库进行第一次扫描，得到频繁1-项集L1；然后，由L1产生C2，并对数据库进行第二次扫描，得到频繁2-项集L2；接着利用上述方法，得到频繁3-项集L3，然后不断重复上述过程，直到找出所有的频繁项集。通过研究分析频繁项集，可以得到用户感兴趣的规则。

显然，对于Apriori算法，存在着如下缺陷[3]：

1）Apriori算法在对候选项集进行模式匹配时，需要对数据库进行多次重复扫描。当数据库规模庞大时，大量的时间将消耗在内存与数据库中的数据的交换上，使得整个扫描过程的时间复杂度很大。

2）算法可能需要产生大量的候选项集。比如说，如果有104个频繁1-项集，那么，就将获得多达107个候选2-项集。

2一种改进的关联规则算法

本文就Apriori算法存在的缺陷，给出一种改进的关联规则算法—GApriori算法。它采用二进制编码技术，算法执行过程中只需扫描一次数据库，能有效地提高数据挖掘的效率。

2.1算法思想

GApriori算法的基本思想：首先对数据库D中的每个数据项进行编码，与此同时，根据每个数据项在数据库中出现的次数获得其支持度计数，从而得到频繁1-项集L1。而由L1得到L2，只需要对L1中项的编码两两进行“与”运算即可。接着由频繁k-项集得到中间频繁项集，将频繁k-项集与中间频繁项集中项的编码作“与”运算，得到频繁(k+1) -项集。重复上述这一步骤，最终得到符合要求的所有频繁项集。采用这种基于编码的方法只需要扫描一遍数据库，且不需要产生候选项集。

由GApriori算法的思想可知，对数据项进行编码是整个算法的基础。下面介绍编码的基本原则：首先要确定编码的长度，这主要取决于D中的事务数。然后，选择一种顺序，对事务进行排序，任一事务仅对应编码中的一位。对于D中某数据项，若出现在某一事务中，则把该事务在此项编码中对应的位取为“1”，相反，取为“0”。比方说，某数据库D共有15个事务(T 1，T 2, T3，……，T15)，项I1分别在事务T 1、T3、T8和T12中出现，那么，相应地可知项I1的编码为(101000010001000)。

该算法主要用到了频繁项集的以下一些性质及推论：

性质1：频繁项集的所有非空子集也一定是频繁的[3]。

利用频繁项集定义，易于得到上述性质，故不再赘述。

由性质1可得到如下性质：如果在数据集D中，X是频繁k-项集，那么，X的任意（k-1）项子集必定是频繁（k-1）-项集。

推论1：如果在数据集D中，Xk是频繁k-项集，那么频繁（k–1）-项集集合Lk-1中包含Xk的（k-1）项子集的个数一定为k[4]。

该推论由上述性质很容易得到。因为Xk的（k-1）项子集个数为k，而Xk是数据集D的频繁k-项集，所以这k个（k-1）项子集都是频繁（k-1）-项集。

推论2：如果在数据集D中，Xk={Xi| 1≤i≤k }是频繁k-项集，那么，对于其任意元素Xi，它在频繁（k-1）-项集集合Lk-1的全部（k-1）项集中出现次数都必定不小于k﹣1次[5]。

证明：因为Xk的（k-1）项子集的个数为k，且由上述性质可知，这k个（k-1）项子集都是频繁（k-1）-项集，因而都包含在Lk-1中。对于Xk的任意元素Xi，它在这k个（k-1）项子集中出现的次数为k-1次。所以，可知结论成立。

2.2算法描述

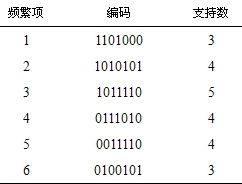
1）扫描事务数据库，对所有事务项进行编码，形成项编码表，统计项的编码中“1”的个数，如果“1”的个数小于事先设定的最小支持度计数，删除该项，得到频繁1-项集L1。

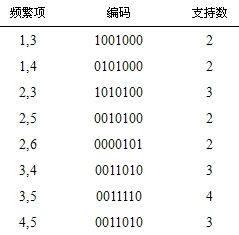
2）将L1中项的编码两两进行“与”运算，对于新得到的编码，统计“1”的个数，如果满足最小支持度计数，那么，这两项就组成频繁2-项集。

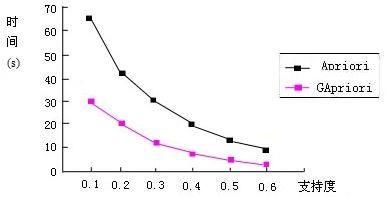
3）设其中一个频繁(k-1) -项集为{Ti，Tj，…Tm}，其中(i

①对Lk-1中每个项出现的次数进行统计，如果出现的次数小于k-1，那么，从Lk-1中删除包含该项的项集，得到Lk-1。同时，由Lk-1中所有项（删除Lk-1中出现次数小于(k﹣1)的项）得到中间频繁单项集LM。这里应用了推论2。

②将Lk-1中项集的编码与LM中项Tn的编码进行“与”运算，对于新得到的编码，如果包含“1”的个数不小于最小支持度计数，那么，将k-项集{Ti，Tj，…Tm，Tn}放到频繁k-项集。否则n=n+1，继续执行第2）步。

4）重复步骤3），直到不能产生新的频繁项集。

2.3算法举例

假设事务数据库D与表1相同。数据库中有7个事务，最小支持数为2。下面演示GApriori算法生成频繁项集的过程。

表1事务数据库D

第一步：对数据库D进行扫描，按照前述编码原则给每个项进行编码，得到项编码表，如表2所示。

表2项编码表

第二步：给每个项目赋一个整数（其中，1对应A，2对应B，依次类推），按照项的编码计数，对支持数小于2的项目进行删除，得到频繁1-项集，如表3所示。

表3频繁1-项集L1

第三步：将频繁1-项集中的项的编码进行两两“与”运算，生成频繁2-项集，如表4所示。

表4频繁2-项集L2

第四步：连接前剪枝，由L2生成L2′和LM，L2中各项出现的次数如表5所示。

表5 L中各项出现的次数

由上表可知，项6在L2中仅出现了1次，小于2，因此，在LM中不包含项6，同时将{2，6}从L2′中删除，不再进行后续连接。第五步：由L2′和LM连接，生成频繁3-项集L3，如表6所示。

表6频繁3-项集L3

第六步：连接前剪枝，由L3生成L3′和LM。

显然，此时L3中每个项出现的次数都小于3，因而L3′为空集。这样搜索过程终止。

3算法评价和性能测试

3.1算法评价

针对前述Apriori算法的不足，GApriori算法做了多方面的改进，具体改进事项如下：

1）与Apriori算法相比，利用GApriori算法生成频繁项集，只需要对数据库扫描一遍，因而效率更高。

2）GApriori算法在生成频繁k-项集时，不再采用频繁(k-1) -项集的自连接。与Apriori算法相比，这会大大减少生成频繁k-项集时所需要连接的项集的数量，同时，生成频繁项集前，无须生成候选项集。

3.2算法性能测试

为了对GApriori算法与Apriori算法的效率进行比较，下面采用相同的条件进行实验。

实验环境：CPU为Pentium 4 /2.0GHz，内存为1G，操作系统为Windows XP Professional。软件采用VC++6.0。

实验数据库：源于一家大型零售超市的销售数据库，共有14580条记录，包含106项。

实验结果如图1所示。

图1两种算法所用时间比较

在图1中，所花费的时间仅仅指算法本身的执行时间，不包括数据的输入输出时间。就算法本身而言，其执行效率与数据的输入输出时间无关，因此，我们在实验中只是对算法本身的执行时间进行测试。

从图1的测试结果中可以得出结论：在支持度相同的情况下，与Apriori算法相比，GApriori算法所用时间更短。并且，支持度越小，GApriori算法的性能越好。

4结束语

本文针对Apriori算法存在的不足，提出了一种新的改进算法—GApriori算法，介绍了该算法的思想和理论依据，并通过具体事例对该算法的执行过程进行了详细说明。最后，对该算法进行了测试，结果表明，该算法具有良好的执行效率。

参考文献：

[1] Agrawal R,Imielinski T,Wami A S.Mining Association Rules Between Sets of Items in Large Databases[C]//Proc. of the ACM SIGMOD Conference on Management of Data,Washington D.C.,1993:207-216.

[2]邵峰晶,于忠清.数据挖掘原理与算法[M].北京:中国水利水电出版社,2003.

[3] Kamber M,Han J.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2007.

[4]颜雪松,蔡之华.一种基于Apriori的高效关联规则挖掘算法的研究[J].计算机工程与应用,2002(10):209-211.

[5]李绪成,王保保.挖掘关联规则中Apriori算法的一种改进[J].计算机工程,2006(7):36-38.