基于相似性的电路力学分析方法

杨 光，杨 硕，倪守诚，田社平

(上海交通大学电子信息学院，上海 200240)

力学反映了最为普遍的自然规律，具有良好的自洽性，特别是拉格朗目(Lagrange)和哈密顿(Hamilton)等人建立起的基于广义力学量的分析力学，可以实现基于结构的相似性有效的理论移植。文献［1］已经给出了力学理论向几何光学的移植，其有效性业已彰现。由于电路模型本质上具有的力学性和形式上与力学理论的相似性，我们将基于集中参数电路基本定理，在集中参数电路中建立起相似于力学的数学模型，从而实现如下的电路分析模式:广义力学模型→电路的力学模型→电路分析方法。这种分析模式将力学理论移植到电路分析中来，提高了理论研究的效率，拓宽了研究思路，对于“基础电路理论”课程的教学颇具意义［2］。

1 广义力学模型

1.1 动力学基本原理和运动方程

动力学基本原理又称达朗贝尔(D'Alembert)原理，是广义力学模型的基础。在自由度为n的力学模型中，达朗贝尔原理表述如下:

式中，qα为广义坐标，互相独立;δqα表示qα的变分;Xα为包含对应qα的所有作用力的总力。考虑到诸δqα互相独立，由式(1)立即可得

上式称为系统的运动方程。式中诸Qk反映了关于qα的各种作用。事实上，如果在一个系统中能够定义满足式(1)的qα和Xα，便可以在这个系统中建立起广义力学模型，用力学方法来对系统的演化规律进行研究［3］。

1.2 拉格朗日方程

对于任意给出的运动方程(1)，一般并非都能定义满足式(4)的拉格朗日函数［4］。

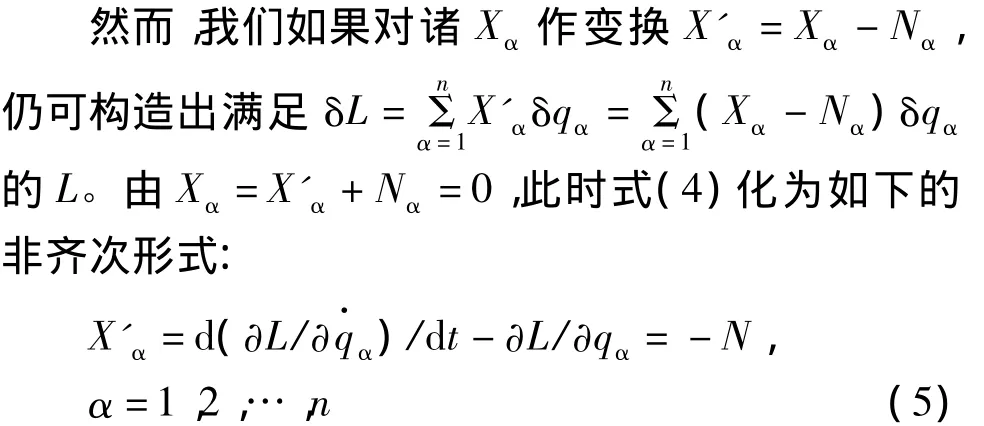
式中，Nα称为广义非势力，是广义力中不能由泛函微商表示的成分。

在系统中建立广义力学模型时，可先通过式(1)进行可行性验证;模型建立后，可通过对式(5)进行分析，确定系统中运动方程的形式，进而确定系统演化所对应的力学分析方法。此外，我们需要指出，以上运算中微分运算的结果亦可包含广义函数，这对应着冲击与碰撞问题。

2 线性非时变电路力学模型的建立

2.1 广义坐标的选取

就本质而言，集中电路参数模型要求将电场和磁场分开［2］，将耗散元件与供能元件分开，即电场和电荷积累只存在于储存电场能的元件中。磁场只存在于储存磁场能的元件中，耗散只存在于阻尼(电阻)元件中，外势场仅由电源决定。

根据上节所述，我们先选取广义坐标，尝试在电路中建立力学模型。

考虑到集中参数电路中的同一支路里，电流处处相等且仅与储存电能的元件里积累的电荷相关，电荷只受接入支路中的电源的作用。同时由于电源都是通过在电路中形成外加势场对电路中电子进行加速，从而实现对电路的供能，这里约定对含有电流源的电路均作戴维南等效。

由电路理论可知，同一支路上元件中电流是互不独立的，它们服从KCL约束，对有N个节点，B条支路的电路，在每一节点处有

式(6)是完整约束［1］。此时互相独立的电流有n=B-N+1个，且n为电路中的独立回路数。考虑到电流的定义i=dq/dt，可以选取n个互相独立的回路电流i1，i2，…，in为对应力学的广义速度，与之对应的电荷量q1，q2，…，qn为对应力学的广义坐标。

2.2 电路的力学原理形式

如上所述，对应力学的广义坐标其量纲为电荷的量纲，即库仑。对照式(1)可知，Xα应具有电压的量纲。于是，将式(1)改写为

如果取Uα为独立回路一周的电压代数和，则由KVL可知

因此力学的式(1)和电路的式(8)的相似性得到了确证，这表明在电路中建立广义力学模型是可行的。

考虑到Uα(α =1，2，…，n)是回路中诸元件两端电压的代数和，按元件的性质将式(9)改写为

式中，UEα、UMα、UNα和USα分别为回路中所有储电能元件两端电压代数和、所有储磁能元件电压代数和、所有耗散元件两端的电压代数和以及所有电源两端的电压代数和。需注意，求和时注意参考方向应取一致［2］。

为了更方便简洁地探究电路的力学对应，考虑最简单的非时变线性模型。此时，储电能元件为线性非时变电容。其两端电压为

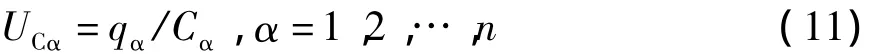
式中，qα为诸元件的电荷积累，Cα为串联电容值。

储磁能元件为线性非时变电感，其两端电压为

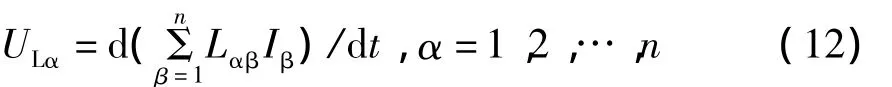
式中，Iβ为产生相应磁场能的电流，Lαβ为串联等效电感矩阵的矩阵元。

电源为线性非时变电源，其两端电压可表示为

2.3 电学量的力学形式对应

从上面的讨论我们初步得到了电学量的两个力学形式，即式(18)和式(19)。除此之外，有一个简单的事实是

根据力学理论，动量是动能对相应速度的微商，则相应的电学理论，便有

上式是关于Iα的自感磁通与互感磁通之和。在力学理论中，动量对时间的微商描述了物体的受力情况，相应地将电路的感性元件视为受力物体，其受力情况如下:

这是感性元件的感应电动势。

将感性元件视为力学的受力质点，继续来研究作用外力的来源。在我们讨论的上述电路系统中，外力只能是由势能产生的保守力和与电阻对应的耗散力，即

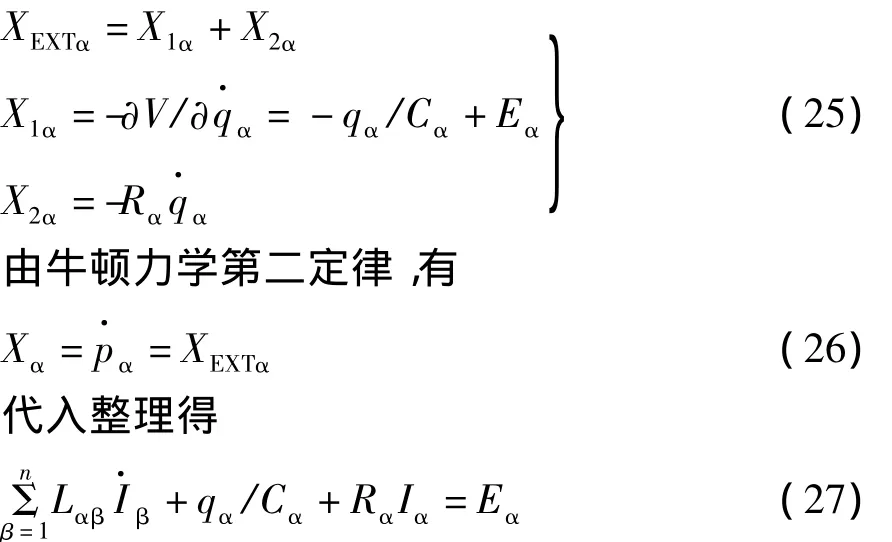
这正是式(10)的结果，进一步表明了电路力学模型的正确性，即确实可以将电压看作广义力来处理。值得一提的是，上述方法均是通过导出力学牛顿运动方程的方法来求解的，而与之等价的则是正则方程。为此，定义哈密顿量为

上式中 Λα(pα)为非正则余项［1］，可由实际计算得出。式(29)的意义将在下面的讨论中体现。

综上所述，线性非时变电路对应的力学模型建立起来了。由于其对应的是线性力学系统，其运动方程将是二阶线性微分方程(组)。在线性动力学中，物体运动的轨迹是唯一的［1］，因此，线性非时变电路的解也具有唯一性。

3 算例

我们现以一个简单的二阶线性电路例子来说明上述分析方法。如图1所示为US激励下的RLC并联电路。

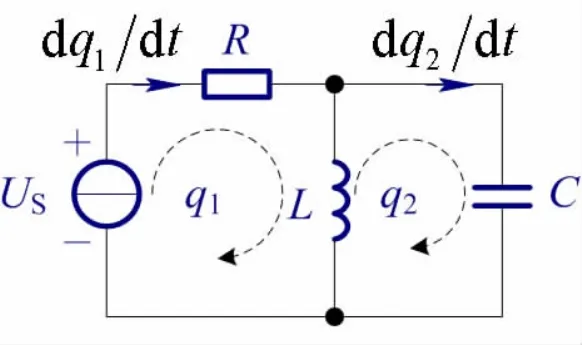
图1 RLC并联电路

我们可以采用如下的分析步骤:

(1)确定电路的自由度:电路的独立网孔数为2，电路的自由度为2。

(2)选取如图1的广义坐标:分别选取电压源—电阻—电感回路和电感—电容回路，含这两个网孔的网孔电荷量q1和q2为广义坐标。

(3)确定拉格朗日量的形式:注意广义速度即电流I1和I2流经电感发生全耦合，电流取图1所示的顺时针参考方向，则有

设iL=I1－I2为电感中电流(参考方向取向下)，uC=q2/C为电容两端电压(参考方向取上正下负)，则上式可化为

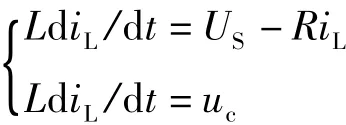
这与列写两个回路的KVL方程结果完全一致。

应用力学模型方法进行电路的分析时，对于符合［式(16)～式(19)］的线性非时变模型电路，我们可以直接列出［式(25)］的拉格朗日方程，从而得到电路力学模型满足的运动方程。然后再进行求解，关于这一点，文献［5］－［8］已经给出了几个有效的算例。需要指出，和力学研究方法相似，电路力学模型着眼于全过程而不区分暂态与稳态，这同传统电路研究方法略有差异。

4 结语

本文指出，从数学上可以发现，线性非时变集中参数电路的力学模型与经典质点动力学模型一一对应关系，如表1所示。这表明，线性非时变电路可借助存在速度反比阻尼的有势质点系模型进行研究。

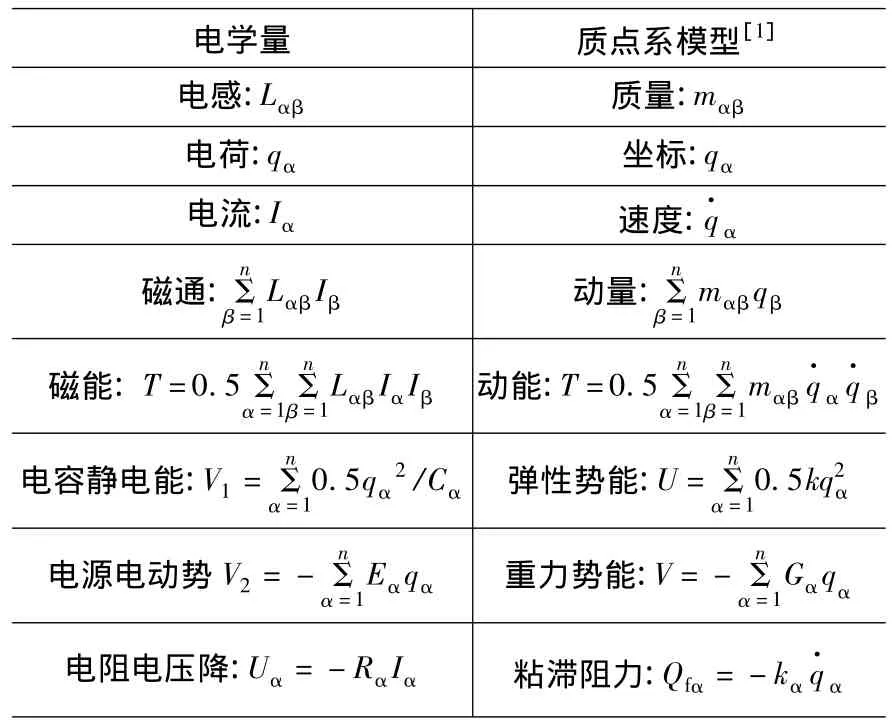
表1 电路的力学模型与经典质点动力学模型

本文初步探讨了电路系统和力学系统的相似性，讨论了广义力学模型在线性非时变电路分析中的应用。通过定义电路中的广义坐标(电荷)和广义速度(电流)，可以为电路建立严格的广义力学模型，即拉格朗日方程组。通过该方程组可推导出电路分析的方程，其结果与应用 KCL、KVL和元件VCR得到的方程完全一致。我们可以受此启发，联想:更复杂的高阶或非线性电路，也一定对应着更加复杂的力学模型。而由于电路系统自身约束具有的完整性，对于任意的电路情形，我们都可以在完整动力学框架下进行探讨。我们对于相似性的讨论，可以有助于在电路教学中开阔电路分析方法的视野。

［1］张启仁.经典力学［M］.北京:科学出版社，2002

［2］陈洪亮，张峰，田社平.电路基础［M］.北京:高等教育出版社，2007

［3］老大中.变分法基础［M］.北京:国防工业出版社，2004

［4］张耀良，刘锡录.关于Lagrange力学逆问题的探讨［J］.哈尔滨:哈尔滨船舶工程学院学报，1993，vol.14(1):102 ～109

［5］赵仁.拉格朗日方法在电路分析中的运用［J］.昆明:云南民族学院学报(自然科学版)，1991，1:vol.8(1):11 ～13，20

［6］刘喜斌.电路中的拉格朗日方程及其应用［J］.北京:工科物理，1998，vol.8(2):4 ～6

［7］姚仲瑜.用拉格朗日方程研究RLC暂态的过程，桂林:广西大学学报(自然科学版)，2001，6，vol.26(2):69 ～73

［8］史玉昌.求解电路系统的另一途径，北京:大学物理，1990，vol.9(12):25 ～ 26