一种基于反步法的移动机器人运动控制算法
段文杰,武颖,刘大亮
(1.山西农业大学 工学院,山西 太谷030801;2.太原理工大学 机械工程学院,山西 太原030013;3.首都航天机械公司,北京100076)
球形机器人[1]、独轮机器人[2]以及双轮机器人[3]的运动控制问题一直是该研究领域的重要内容[4]。多数情况下,在平面内,这3类机器人的运动可以简化为一均质圆盘的垂直滚动。本文首先利用拉格朗日方法[5]建立均质圆盘垂直滚动的一阶链式非完整系统模型;其次利用反步法[6~8]设计系统的稳定运动控制算法,并证明了算法是渐进稳定的。状态镇定和路径跟踪仿真实验结果表明该算法是有效的、可行的。
1 系统建模
如图1所示,圆盘的位形由坐标平面上的位置x和y,进动角θ和圆盘的自转角ψ确定,记为q=(x,y,ψ,θ)。圆盘的半径为r。对圆盘施加的力矩分别为绕铅垂轴的转向力矩τ1和自转动力矩τ2。圆盘作无滑动的纯滚动,该速度约束可以表示为

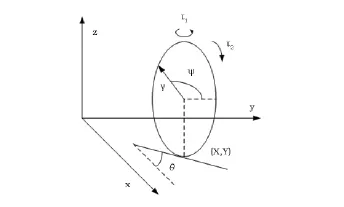
图1 系统坐标系与运动模型Fig.1 Coordinate system and motion mode
记m为圆盘的质量,J1,J2分别为关于铅垂轴和水平滚动轴的转动惯量,则系统的拉格朗日函数[9,10]为

其中,常值惯性矩阵 M =diag(m,m,J1,J2)。经计算得到系统的动力学方程为
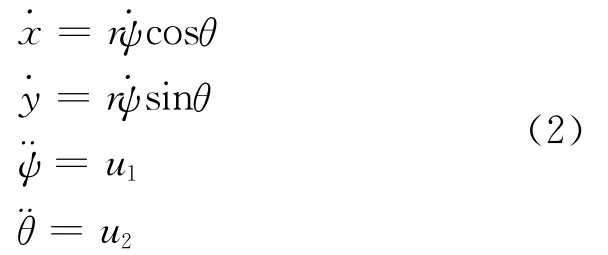
其中ui=τi/Ji,i=1,2。如果系统的输入控制表示为˙ψ=ω1和˙θ=ω2,通过对半径r的单位正则化处理后,运动学形式的模型可以表示为
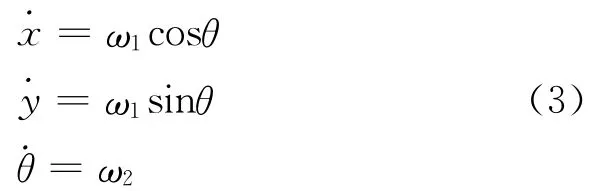
在θ∈(-π/2,π/2)上,应用坐标和输入控制变换

可以得到一个一阶链式非完整系统

2 运动控制算法
定理:存在时不变且有界的状态反馈
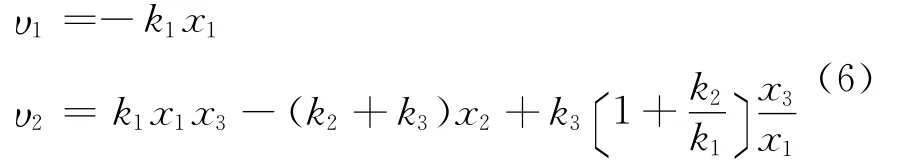
在

上,当t>0时,系统(5)的状态x指数收敛至零。其中k1,k2和k3为正数,且k3>k1。
证明:应用线性状态反馈

使x1指数稳定,其中k1为正常数。系统(5)变为
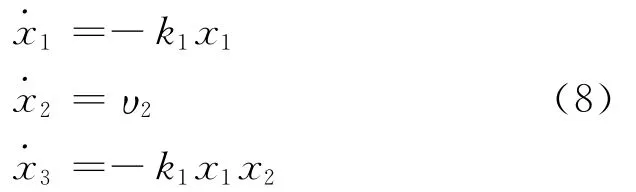
考虑x3子系统,将x2看成是Ω上的输入控制,设计反馈控制
3)资源丰富,情境真实。微课的核心就是视频的展现和多媒体课件,里面包含专家的点评和教学反思,还有练习和测验,可以给学生创设一个具象化的情境。微课的这一特点在国内外的微课交流平台上都展现出来。当前微课不应只是视频资源,还要将微课平台发展成一个互动性教学平台,不光有练习和测验,还要有知识讲解、学习反馈等资源,这些配套的资源能对学生自主学习发挥重要作用[4]。
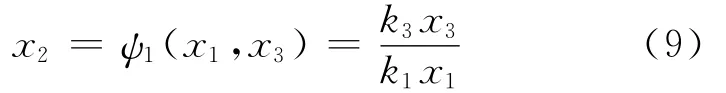
以稳定原点x3=0,其中x1不为零。取Lyapunov函数V1为
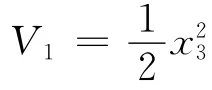
上式对时间的导数得
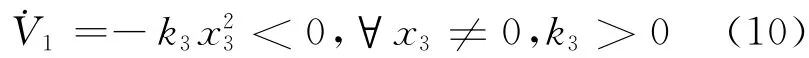
因此,˙x3=-k3x3的原点是渐近稳定的。应用微分同胚变量代换

对(11)求导得
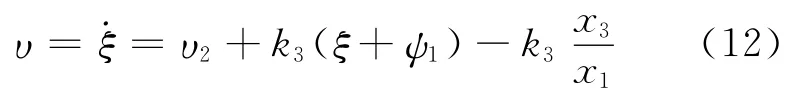
则x2和x3子系统变换为
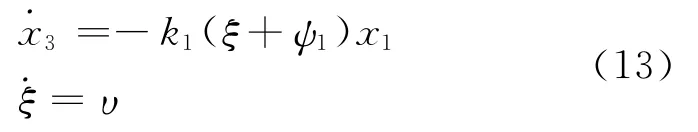
取Lyaponov函数V2为
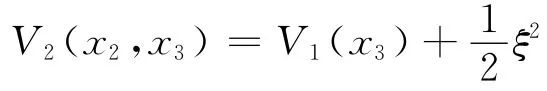
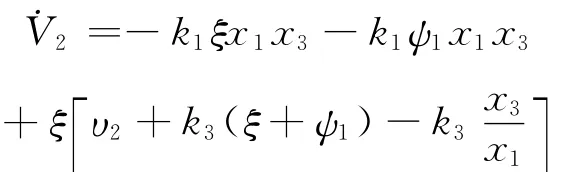
取
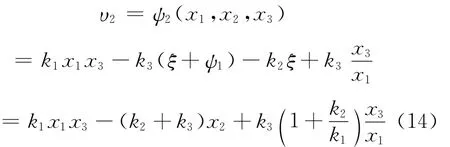
从而得

则x3和ξ是有界的,且当t→0时趋近于零。因此,x2收敛于ψ1。
为了保证x2的有界性和关于零的收敛性,当t→0时必须保证x1和x3的有界性和关于零的收敛性。因为
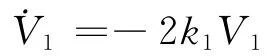
可知当t→∞时,V1以解e-2k3t收敛到零,x3以解e-k3t收敛到零。又因为x1以解e-k1t收敛到零,可知当k3>k1时,且x1(0)≠0时,x3/x1是有界的,以解e-(k3-k1)t收敛到零。
当初始条件始于Ω,状态反馈(6)不仅保证了系统状态的有界性,而且原点是指数收敛。如果系统始于Ω的外部时,可以在任意小的时间内应用开环控制驱动系统从x1=0点进入Ω内,再切换至状态反馈(6)。
3 仿真实验
图2和图3为在控制率(6)的作用下,系统(5)状态的收敛特性。系统初始状态为x(0)=(x10,x20,x30)=(0.5,-1,1),位于集合 Ω内。控制率的控制参数为k1=5,k2=5和k3=10。如图所示,系统在控制率(6)的控制作用下,状态能够渐近收敛到零,因此控制算法是有效的。

图2 状态响应曲线Fig.2 Response curve of state

图3 运动轨迹响应曲线Fig.3 Response curve of motion trace
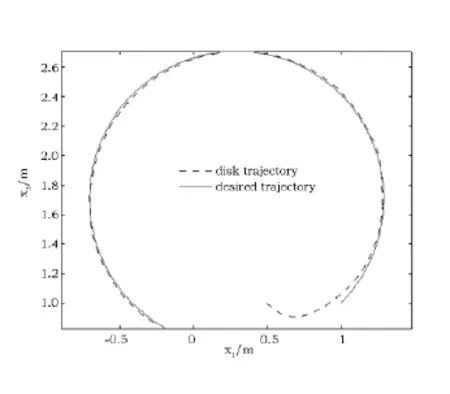
图4 圆周曲线跟踪曲线Fig.4 Tracking curve of circular curve
状态反馈控制率(6)可以应用于垂直圆盘的轨迹跟踪控制,即使状态(x1,x3)收敛到期望的状态(x1d,x3d)。一个期望的圆周曲线满足方程

其中期望轨迹的线速度和角速度分别为ur=0.5m·s-1,rr=0.5rad·s-1。系统初始状态为x(0)=(x10,x20,x30)=(0.5,-1,1),位于集合Ω内。期望轨迹的初始状态为 (x1d,ψd,x3d)=(1,π/4,1)。控制率的控制参数为k1=5,k2=5和k3=10。系统轨迹跟踪特性如图4所示,控制算法(6)能够实现对期望轨迹的跟踪。
4 结论
本文将球形机器人、独轮机器人和双轮机器人的一种运动方式简化为均质圆盘在平面内的垂直滚动,首先建立了系统的链式非完整模型,其次利用反步法设计运行控制算法,并证明了反馈控制系统的原点是渐进稳定的。仿真结果表明控制算法是可行、有效的。
[1]刘大亮,孙汉旭,贾庆轩.一种球形移动机器人的非线性滑模运动控制[J].机器人,2008,30(6):498-502.
[2]Shao Zhiyu,Liu Daliang.Balancing Control of a Unicycle Riding[C].In:CCC10,29th Chinese Control Conference,Beijing,China,2010:3250-3254.
[3]刘大亮,孙汉旭.一种可载人行走的双轮机器人[J].机器人,2009,31(5):416-420.
[4]许国保,尹怡欣,周美娟.智能移动机器人技术现状及展望[J].机器人技术及应用,2007,3月31日:29-34.
[5]Murray R M,Li Zexiang,Sastry S S.机器人操作的数学导论[M].北京:机械工业出版社,1998:56-78.
[6]Riccardo Marino,Patrizio Tomei,著,姚郁,贺风华,译.非线性系统设计——微分几何、自适应及鲁棒控制[M].北京:电子工业出版社,2006:121-143.
[7]焦晓红,关新平.非线性系统分析与设计[M].北京:电子工业出版社,2008:132-136.
[8]方勇纯,卢桂章.非线性系统理论[M].北京:清华大学出版社,2009:101-124.
[9]叶敏,肖龙翔.分析力学[M].天津:天津大学出版社,2001:65-67.
[10]王振发.分析力学[M].北京:科学出版社,2011:78-82.

