加权质心定位误差的反向修正法*

孙玮琢，迟 卫，王擎宇

(海军大连舰艇学院航海系，大连116018)

质心定位算法(CL)［1］是无线传感器网络节点定位算法中的一种无需测距的算法，它把能够与未知节点进行通信的锚节点所组成的多边形的质心(以下简称多边形质心)确定为未知节点的估计位置，具有计算简单、对硬件要求低等优点，但同时也存在精度较低，需要较高锚节点密度等问题。为此，国内外大量研究人员又研究了多种质心定位算法的改进算法［2－12］，加权质心定位算法(WCL)就是其中重要的一类，它的基本思想是为每个锚节点设定一个权值，以表征未知节点与锚节点之间的距离关系，使未知节点的估计位置更接近距其较近的锚节点，远离距其较远的锚节点，从而使估计位置比多边形的质心更接近真实位置，在一定程度上提高了定位精度、降低了锚节点密度。

然而，加权质心定位算法的精度仍然受到多个方面因素的影响，它们包括权值函数的距离因子、未知节点自身位置、锚节点分布情况、以及未知节点与锚节点间的距离等。本文主要针对距离因子和未知节点自身位置这两个因素展开研究，详细分析这两个因素对定位精度的影响，并提出一种从定位结果出发的反向修正法用于提高WCL算法的定位精度。

1 加权质心定位算法

设锚节点的坐标为Bj(x，y)，未知节点的真实位置为Pi(x，y)，估计位置为P'i(x'，y')，根据质心定位算法(Centroid Localization，CL)则有式(1)

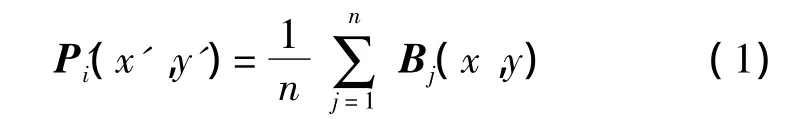
其中，n为能够与未知节点进行通信的锚节点数量。

在质心定位算法的基础之上，为每个锚节点加上一个权值wij就得到了加权质心定位算法WCL(Weighted Centroid Localization)，根据 WCL算法得到式(2)

为研究定位精度，本文将定位误差定义为:

横、纵坐标的误差定义为:

本文所有仿真实验均利用Matlab7.1实现，距离单位设为1，仿真区域为100×100的矩形，矩形的4个顶点上各有1个锚节点，每个锚节点的通信半径为150，能够覆盖该矩形区域，并且在所有仿真实验中都令权值函数中的距离值为未知节点与锚节点间的准确距离。

图1为WCL与CL的定位精度对比图，“圆圈”表示未知节点的真实位置，坐标为(30，15)。“方块”表示利用CL算法得到的估计位置，坐标为(50，50)，误差超过了40.0。“星号”表示利用WCL(g设定为2)算法得到的估计位置，坐标为(22，16)，误差为8.5。由此可见，WCL算法的定位精度要远远高于CL算法。

图1 CL与WCL的精度对比

2 距离因子g对定位精度的影响及全局最优g的选取

2.1 距离因子g对定位精度的影响

在WCL算法中，距离因子需要人为设定，不同的距离因子会使定位结果产生较大差异。为此，利用仿真实验详细研究了不同的距离因子对定位精度的影响。具体方法是:从0到10每隔0.01取一个值赋给g，并计算未知节点的估计位置，从而观察估计位置随g变化的规律。本文将误差最小的估计位置(最优位置)对应的g称为该未知节点的最优g。

如图2所示，圆圈为一个真实位置是(30，15)的未知节点，g从0到10逐渐增大，该节点的估计位置便随之由矩形质心逐渐靠近离该节点最近的锚节点，此过程中误差先由大变小，当到达最优位置时，误差最小，然后误差又逐渐增大。连接所有估计位置形成一条曲线，图中的线段为真实位置与最优位置之间的连线，该未知节点所对应的最优g为1.72。如果未知节点的真实位置发生变化，其对应的最优g和最优位置也随之发生变化，如图3所示。

图2 坐标为(30，15)的未知节点选取最优g的示意图

图3 不同位置的未知节点选取最优g的示意图

2.2 全局最优g的选取

由于每个最优g只能使某一位置上的未知节点的定位误差达到最小，而不能使区域内所有位置上的未知节点的定位误差达到最小，所以必须选取一个全局最优g。为此，本文采用的方法是:首先，对该区域进行大量采样，由于该区域为正方形，具有轴对称性，所以将采样区域缩小至(0，0)、(50，0)和(50，50)为顶点的三角形区域(图4中的1区)，采样点横纵坐标的范围均为(0，50］，间隔为1。然后，从0到10每隔0.01取一个值赋给g，并计算全体采样点的平均定位误差，最后将最小平均定位误差对应的g作为该区域的全局最优g。仿真结果如图5所示，曲线表示平均定位误差随g的变化规律，当g等于1.82时平均定位误差达到最小值7.2，所以仿真区域的全局最优g为1.82，下文中的仿真将全部以1.82作为WCL算法的距离因子。

图4 定位区域分隔示意图

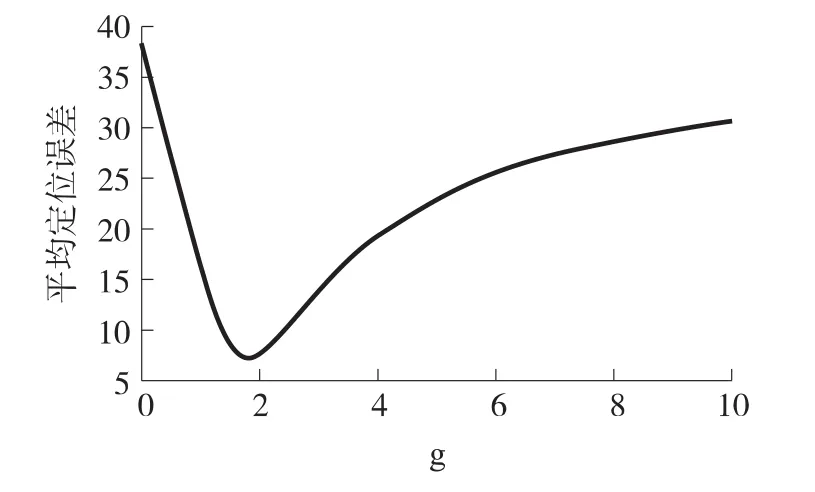
图5 平均定位误差随g的变化规律

3 未知节点自身位置对定位精度的影响及误差的反向修正法

3.1 未知节点自身位置对定位精度的影响

选取了全局最优g之后，又进行了对比仿真实验，如图6和图7所示，它们分别为g=4时和g=1.82时全区域的定位误差示意图，“圆圈”表示节点真实位置，由“圆圈”出发的线段终点表示节点估计位置。显然，采用全局最优g时质心附近区域的定位精度得到了显著提高，但是远离质心区域的定位精度却仍然比较差。为此，对采样区中的全部采样点逐一进行了计算，结果表明，采用全局最优g之后，当未知节点处于质心附近区域时，定位精度较高，最小误差为0，而当未知节点处于远离质心的区域时定位精度则较差，最大误差可达18.8。由此可见，虽然对距离因子g进行了优化，但是未知节点自身位置仍然可对定位精度造成较大影响，特别是当未知节点处于远离质心的区域时，定位误差非常大。如果能够适当消除由节点自身位置所致的误差，必将有效减小远离质心区域的定位误差，进一步提高WCL的定位精度。

图6 当g=4时全区域的定位误差示意图

图7 当g=1.82时全区域的定位误差示意图

3.2 误差的反向修正法

目前，WCL算法的改进方法多为通过优化权值函数或权值函数中的参数来减小误差，即正向修正。本文提出一种误差的反向(Error Back，EB)修正法，该方法利用估计位置与误差之间的近似关系，根据WCL的定位结果求得近似误差，然后对定位结果进行修正，从而提高定位精度。它的具体流程如图8所示，共分五个步骤:

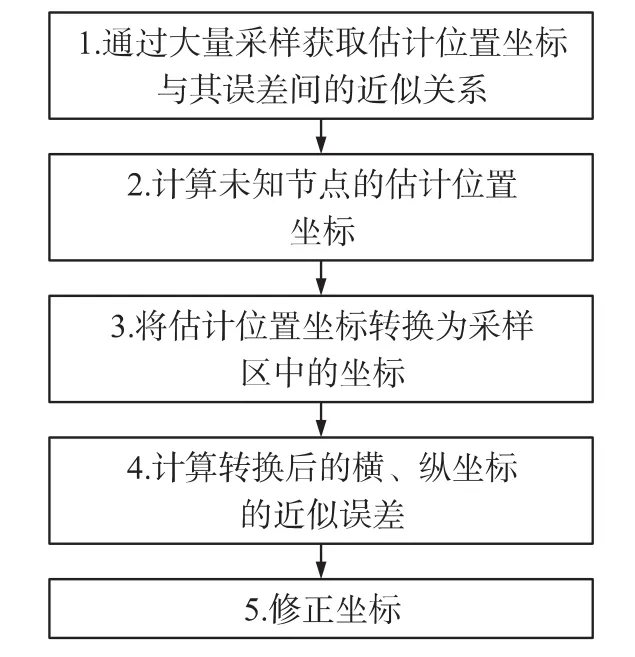
图8 误差反向修正法的流程图

第一步是通过大量采样获取定位区域内估计位置坐标与其误差之间的近似关系，这是该修正法的基础，具体方法为:以采样区中的全部采样点为对象，利用式(2)计算出它们的估计位置，利用式(4)、式(5)计算出估计位置的横、纵坐标误差，然后利用Matlab中的曲线拟合函数polyfit求得采样点估计位置的横、纵坐标与其误差之间的近似关系。图9为估计位置横坐标与其误差之间的近似关系曲线，图10为估计位置纵坐标与其误差之间的近似关系曲线。

图9 估计位置横坐标与其误差之间的近似关系

图10 估计位置纵坐标与其误差之间的近似关系

第二步是利用式(2)计算未知节点的估计位置坐标(x'，y')。

第三步是将估计位置坐标转换为采样区(图4中的1区)中的坐标。这是因为，第一步中求得的近似关系只适用于采样区，若要利用这种关系对处于其他区域的节点进行误差修正，必须先将未知节点的估计位置坐标转换成采样区中相对应的坐标。具体方法为:首先判断估计位置坐标处于图4中的哪个区域，然后依照表1中的规则将其转换为采样区的坐标(x，y)。

表1 坐标转换规则

第四步是计算转换后的横、纵坐标的近似误差，具体方法为:将转换后的横、纵坐标分别代入第一步中求得的近似关系中，计算出转换后的横、纵坐标的近似误差。

第五步是修正误差。首先用第四步中求得的近似误差修正转换后的坐标，然后依照表1中的规则将修正后的坐标转换成估计位置所在区域内的坐标。

上述流程中，第一步是定位前的准备工作，第二步至第五步是具体的定位过程。由于并不是所有的定位区域都能通过大量采样计算估计位置坐标与其误差间的近似关系，因此EB修正法存在一定的局限性，研究发现，当定位区域形状较规则、估计位置坐标与其误差之间存在较明显的近似关系时，才能够通过大量采样计算这种近似关系，进而利用EB修正法对WCL算法的计算结果进行修正。

通过对采样区全体采样点的计算，结果表明，使用EB修正法后最小定位误差仍为0，但最大定位误差已缩小至13.5，平均定位误差也由7.2缩小至3.5，全区域的定位误差如图11所示。从计算结果和示意图中可以发现，EB修正法在保持质心附近区域定位精度基本不变的同时，有效地缩小了远离质心区域的定位误差，较大幅度地提高了WCL的定位精度。

图11 EB修正法修正后的定位误差示意图

4 结论

EB修正法是一种从定位结果出发的反向修正方法，它能有效减小WCL算法的定位误差。使用EB修正法之前需要根据定位区域的形状、各类节点的性能以及锚节点的分布情况计算全局最优g，以及定位区域内估计位置坐标与其误差之间的近似关系，因此该方法比较适合用于定位区域的形状比较规则且锚节点位置固定不变的情况。此外，本文只提出了理想条件下的EB修正法，并没有研究锚节点与未知节点间的距离误差以及锚节点分布情况对该方法的影响，后续工作将重点研究这两个问题，并提出相应的解决方案。

［1］ Bulusu N，Heidemann J，Estrin D.GPS-Less Low Cost Outdoor Localization For Very Small Devices［J］.IEEE Personal Communications Magazine，2000，7(5):28－34.

［2］ Blumenthal J，Reichenbach F，Timmermann D.Position Estimation in Ad hoc Wireless Sensor Networks with Low Complexity［C］//Proceedings of the 2nd Workshop on Positioning，Navigation and Communication and 1st Ultra-Wideband Expert Talk.Hannover:2005.41－49.

［3］ Blumenthal J，Grossmann R，Golatowski F，et al.Weighted Centroid Localization in Zigbee-based Sensor Networks［C］//IEEE International Symposium on Intelligent Signal Processing，2007.WISP 2007.Alcala de Henares:IEEE，2007.1－6.

［4］ Blumenthal J，Reichenbach F，Timmermann D.Precise Positioning with a Low Complexity Algorithm in Ad hoc Wireless Sensor Networks［J］. Praxis der Informationsverarbeitung und Kommunikation，2005，28(2):80－85.

［5］ Reichenbach F，Timmermann D.Indoor Localization with Low Complexity in Wireless Sensor Networks［C］//2006 IEEE International Conference on Industrial Informatics.Singapore:IEEE，2006.1018－2023.

［6］ 李兆斌，魏占祯，徐凤麟，等.无线传感器网络增强的质心定位算法及性能分析［J］.传感技术学报，2009，22(4):1247－1250.

［7］ 林玮，陈传峰.基于RSSI的无线传感器网络三角形质心定位算法［J］.现代电子技术，2009，32(2):180－182.

［8］ 朱建新，高蕾娜，张新访.基于距离几何约束的二次加权质心定位算法［J］.计算机应用，2009，29(2):480－483.

［9］ 郜丽鹏，朱梅冬，杨丹.基于ZigBee的加权质心定位算法的仿真与实现［J］.传感技术学报，2010，23(1):149－152.

［10］刘运杰，金明录，崔承毅.基于RSSI的无线传感器网络修正加权质心定位算法［J］.传感技术学报，2010，23(5):717－720.

［11］朱博，陈曙.一种无线传感器网络质心定位改进算法［J］.传感技术学报，2010，23(6):868－872.

［12］程伟，史浩山，王庆文.一种无需测距的无线传感器网络加权质心定位算法［J］.西北大学学报(自然科学版)，2010，40(3):415－418.