改进的SURF 算法及其在目标跟踪中的应用

刘少鹏，郎跃东，丁祝顺

(北京航天控制仪器研究所，北京100039)

0 引 言

基于局部不变特征匹配的目标跟踪算法得到了广泛研究。作为性能最好的局部不变特征之一，SURF 特征描述子应用在目标跟踪中也获得了良好的效果［1～3］。

与 GLOH，SIFT［4，5］等经典局部不变特征描述子相比较，SURF 具有区分度好，运算速度快等优点。但是在描述子生成阶段，SURF［6］需要求取特征点邻域像素的主方向，在区域内以主方向为基准求取采样点的Haar 小波响应，从而生成局部特征描述子，运算过程包含大量浮点运算，并且逻辑复杂，优化难度大，基于SURF 的算法难于在嵌入式系统中实时实现。而在实际应用中目标跟踪算法常常需要在嵌入式系统中实现，这也限制了SURF 特征描述子更广泛的应用。

针对以上问题，本文利用三角和对角线特征对SURF特征描述子生成过程进行了改进，避免了对特征点邻域像素的Haar 特征求取与Haar 小波向主方向旋转的运算。所提算法保留了SURF 算子的旋转、尺度不变性，对模糊图像的特征点匹配性能更好，简化了实现过程，有效提高了运算速度，可以满足目标跟踪算法的应用要求。

1 SURF 特征描述子介绍

基于SURF 的特征点［7］匹配主要包括3 个步骤:1)SURF 特征点检测;2)SURF 特征描述子生成;3)前后帧特征描述子匹配与提纯。本文对SURF 算法的改进主要体现在SURF 特征描述子生成方面。首先利用SURF 特征点检测算法获取SURF 特征点。在获取图像特征点后，求取特征点邻域主方向，以特征点为中心，沿主方向构建一个正方形区域，区域尺寸大小为20 s ×20 s，s 为特征点的尺度值。将此区域分为4 ×4 个子块，每个子块中有5 s×5 s 个像元，使用尺寸2 s 的Haar 小波滤波器对子块内的图像进行小波响应计算，共进行25 次采样计算，分别得到以主方向为基准的dx 和dy 响应。如图1 所示。

图1 特征描述子求取Fig 1 Calculation of SURF descriptor

然后，以特征点为中心，对dy 和dx(以主方向为基准)进行高斯加权计算(σ=3.3 s)。最后对每个子块的小波响应进行统计，为了体现不同的极性，同时也对每个子块小波响应的绝对值进行统计，得到每个子块的特征矢量

V= ［∑dx，∑ | dx|，∑dy，∑ | dy|］.

由于共有4 ×4 个特征子块，因此，特征描述子为一个4 ×4 ×4 =64 维的特征矢量，即为特征点的描述表达。

为了简化运算，SURF 特征描述子在积分图像中利用盒子算法求取水平和垂直方向的Haar 响应，然后根据主方向对dx 和dy 进行旋转，即得到旋转后的Haar 小波响应。

为了求得旋转后的Haar 小波响应，需要将旋转前的点坐标进行二维旋转［3］。如图2 所示，旋转前图像坐标为(l，k)，旋转后坐标为(x，y)，旋转后的坐标可以通过坐标旋转公式得到

得到点(l，k)在旋转后图像中的坐标(x，y)后，利用积分图像求得水平和垂直方向的 Haar 小波 dx'，dy'，对 dx'，dy'进行加权处理，并将dx'，dy'按照式(2)旋转到特征点主方向，从而得到旋转后的dx，dy。

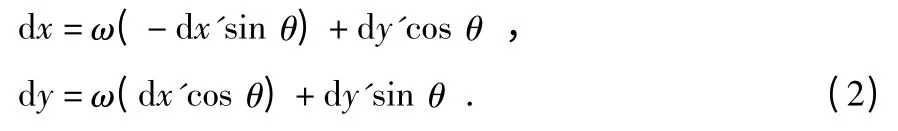
2 改进的SURF 算法

针对SURF 算法需进行坐标旋转和特征点计算优化难度大等问题，本文利用三角特征和对角线特征设计了改进的SURF 特征描述子，利用子块的三角特征和对角线特征取代图1 所示子块内像素的Haar 小波特征，图像子块三角算子和对角线算子的实现如图3 所示。

图2 利用积分图像求取Haar 响应示意图Fig 2 Diagram of obtain Haar response using integral image

图3 利用三角、对角线特征生成描述子Fig 3 SURF descriptor generation using triangle and diagonal featrues

与标准SURF 算法类似，三角算子和对角线算子实现同样需要在每个图像子块内取25 个采样点，但是不对采样点求Haar 小波，而是对25 个采样点应用图3 中所示三角算子和对角线算子来表示每个图像子块的局部特性，同样每个图像子块可以得到一个四维的描述矢量

V=［T1T2C1C2］.

T1，T2分别对应图3 中对图像子块运用2 个三角算子得到的结果，C1，C2分别表示对图3 中图像子块运用对角线算子得到的运算结果。

以三角算子计算为例，求取过程如图4 所示。图4 左图为旋转后的图像，如欲求取某子块的三角特征，须首先利用式(1)获取旋转后的坐标值(x1，y1)和(x2，y2)，并根据(x1，y1)和(x2，y2)的坐标所属区域分别乘以三角算子对应的正负系数，然后进行累加，即得到某子块的一个三角算子描述。

如上所述，在计算图像子块的三角特征和对角线特征时，只需将图像的灰度值乘以对应的系数后直接进行累加运算，图像的灰度值为标量，不存在旋转的问题，避免了x和y 方向的Haar 小波求解和旋转操作，节约了大量浮点运算的运算量。

类似可以获得另外一种三角算子和2 个对角线算子的特征表示。

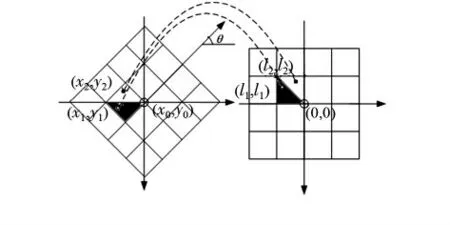
图4 图像子块三角特征求取示意图Fig 4 Calculation diagram of triangle feature of image sub-block

3 算法性能测试

3.1 匹配测试

本文对SURF 和改进SURF 算法的匹配效果进行了测试;测试主要包括旋转、模糊和缩放。

测试图片如图5 ～图7 所示。每组图中，第一张图为基准图，后续图片为相对原图发生旋转、模糊以及缩放等变化的图片。因为每组图片较多，图中所示仅为部分图片，以作示意。图8 ～图10 为测试结果，其中，实线表示本文改进SURF 算法的测试结果。

图5 旋转测试图片Fig 5 Images of rotation test

图6 模糊测试图片Fig 6 Images of blur test

图7 尺度变化测试图片Fig 7 Images of scale variation test

图8 旋转图像匹配比较Fig 8 Matching comparison of rotation images

图5 为对旋转不变性进行测试所用的图片，测试图片旋转角度分别为 10°，20°，直到 80°。从图 8 中可见 2 种算法都出现了旋转角度变大时，匹配点数反而增加的情况。这说明所谓旋转不变并不是完全不受旋转影响。通过对SURF 特征算子提取过程，以及随图片旋转，特征点数量发生变化的情况进行分析可以发现，SURF 算法的旋转不变性体现在描述子生成阶段，而在 SURF 特征点［6，7］检测阶段仍然受到旋转影响，即旋转有可能影响某一像素点是否是SURF 特征点，同时也可能影响SURF 特征点的尺度。因此会造成随旋转角度不同，特征点匹配数目发生变化的情况，从而间接影响了旋转图像中特征点的匹配数目。

对比2 种算子的匹配点数，可看到改进SURF 的性能在旋转角度小于40°时匹配效果和SURF 算法接近，但随旋转角进一步变大，改进SURF 的效果较经典SURF 算法略差。这说明在相同匹配准则下，三角算子和对角线算子构建的SURF 特征描述子对旋转图像的区分能力略低于经典SURF 特征描述子。

对比图8 中的匹配准确率，可见两者的匹配准确率基本相当。

图9 为对模糊图片进行特征点匹配的匹配结果。可以看到，随着模糊程度的加深，2 种特征描述子的匹配点数均发生下降，匹配准确率也发生下降。对比2 种特征描述子匹配的具体数据可见，改进的SURF 特征描述子不论在匹配点数和匹配精度方面均显著高于经典SURF 特征描述子。经典SURF 特征描述子基于Haar 小波构建，Haar 小波体现了像素的边缘特征，而随着模糊程度加深，图像的边缘特征逐渐变得不明显。因此，经典SURF 算子性能出现了下降，而改进的SURF 算子中的三角和对角线特征，主要体现了特征点邻域子窗口的整体特征，受局部像素点边缘模糊影响较小，性能下降程度要小于经典SURF 算子。

图10 为对尺度变化进行测试的结果，从图中可以看到，改进的SURF 算子匹配点数略低于经典算子，而匹配准确率则与经典算子十分接近。这说明虽然改进的SURF 特征描述子对尺度变化特征的区分能力略有下降，但是仍然保留了尺度不变性的特点。

图9 模糊图像匹配比较Fig 9 Matching comparison of blur images

图10 尺度变化图像匹配比较Fig 10 Matching comparison of scale variation images

3.2 计算复杂度测试

本文对SURF 算子的改进主要目的是嵌入式应用，因此，将SURF 算子和改进的SURF 算子计算移植到主频为1GHz 的TMS320C6416 处理器中实现，采用相同的优化策略，以比较改进算法和经典算法的运行速度。测试过程对相同视频图像求SURF 特征点，并计算特征点的特征描述子，实验过程中将特征点数量设定为60 个。测试结果表明:改进SURF 算法实现了28f/s 的运算速度，而标准SURF算法运算速度约为19f/s。采用三角特征和对角特征对SURF 算法进行改进后，运算速度提高了约47%。

从3.1，3.2 小节的测试结果来看，改进SURF 特征描述子保留了经典SURF 特征描述子的旋转、尺度不变性，对模糊图像鲁棒性增强，运算速度有了显著提升，比经典SURF特征描述子更适合嵌入式系统应用。

4 目标跟踪应用实验

为了验证改进的SURF 特征描述子实际应用效果，基于SURF 特征点匹配设计了目标跟踪策略，以验证改进SURF 特征描述子在目标跟踪中的应用效果。

手动控制波门锁定跟踪区域，然后控制目标区域移动，移动包括平移、旋转以及视角变化等。跟踪过程视频截图如图11、图12 所示。

图11 改进的SURF 特征描述子跟踪试验1Fig 11 Tracking test 1 for improved SURF feature descriptor

图12 改进的SURF 特征描述子跟踪试验2Fig 12 Tracking test 2 for improved SURF feature descriptor

图11 中目标在移动过程中发生了角度旋转和比较严重的模糊，但是跟踪波门始终锁定在正确的位置上，实现了在目标快速移动中的跟踪功能。充分证明了改进算子在图像旋转和模糊情况下的鲁棒性。

图12 中目标首先发生了角度旋转，到第716 帧时和初始情况相比，目标旋转角度、视角、尺度均发生了较大变化，第850 帧目标在尺度上又回到和第一帧接近的状态，但是仍然存在旋转角度的差异。整个过程波门始终锁定在正确位置上，证明了算子在目标旋转和尺度发生变化情况下的有效性。

5 结束语

针对SURF 特征描述子运算复杂，难于满足嵌入式系统实时运算要求的不足，对SURF 特征描述子提取算法进行了改进。利用三角特征和对角线特征设计了新的SURF特征描述子。对2 种算子的匹配性能和运行速度进行了对比分析，充分讨论了改进SURF 特征描述子的优势和不足。利用改进的SURF 特征描述子设计了目标跟踪算法，通过实验验证了改进SURF 特征描述子在目标跟踪应用中的有效性。

［1］ Miao Quan，Wang Guijin，Shi Chenbo.A new framework for online object tracking based on SURF［J］.Pattern Recognition Letters，2011，31:1564 －1571.

［2］ 周志强，汪 渤.尺度不变特征在自主寻的电视制导中的应用［J］.电光与控制，2009，16(9):6 －8.

［3］ 王永明，王贵锦.图像局部不变特征与描述［M］.北京:国防工业出版社，2010.

［4］ Mikolajczyk K，Schmid C.A performance evaluation of local descriptors［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(10):1615 －1630.

［5］ Lowe D G.Object recognition from local scale－invariant features［C］∥Proceedings of the International Conference on Computer Vision，Corfu，Greece，1999:1150 －1157.

［6］ Herbert Bay，Tinne Tuytelaars，Luc Van Gool.SURF:Speeded up robust features［C］∥Lecture Notes in Computer Science，Graze:ECCV，2006:404 － 417.

［7］ Herbert Bay，Andreas Ess，Tinne Tuytelaars，et al.Speed－up robust features(SURF)［J］.Computer Vision and Image Understanding，2008，110(3):346 －359.