基于Monte Carlo的行程时间可靠性研究＊

张雄飞 李瑞敏 李宏发 史其信

（清华大学交通研究所1） 北京 100084） （中国民航大学空中交通管理学院2） 天津 300300）

行程时间可靠性是指对于给定的起终点之间，出行者能在规定时间内顺利完成出行的概率［1］，行程时间可靠性可分为路段行程时间可靠性、路径行程时间可靠性、OD对行程时间可靠性以及系统行程时间可靠性［2］.由于直接采集路径行程时间数据比较困难，因此，对路径行程时间可靠性的研究一般建立在对路段行程时间特征分析的基础上.以往的研究通常假设路段行程时间服从相互独立的正态分布，则路径行程时间也服从正态分布［3－4］.而实际上，路段行程时间之间具有相关性，也不一定服从正态分布，分布特性也可能各不相同［5－6］，从而使得基于解析方法求解路径行程时间特性比较复杂.交通学者也认识到行程时间可靠性对出行者路径选择的重要影响［7－9］.事实上，行程时间可靠性与出行者路径选择是一个相互作用的过程，行程时间可靠性的改变带来出行者路径选择的改变，从而导致路段流量的变化，最终引起行程时间可靠性的改变.本文从出行者的角度出发，将路段通行能力作为连续随机变量，对行程时间可靠性进行定义，并用Monte Carlo法进行求解，同时考虑行程时间可靠性对交通流量分布的影响.

1 行程时间可靠性

行程时间可靠性根据其定义，可用以下一般公式表示

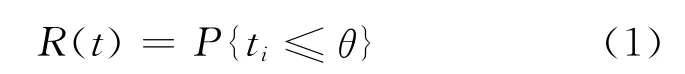
式中：R（t）为指定路段、路径或者OD对之间行程时间可靠性；ti为第i次出行在指定路段、路径或者OD对之间所花费的时间；θ为指定的行程时间阈值，θ一般可取.其中：为对应的自由流行程时间；φi为对现实状况的期望指标，为大于1的实数.

从上述定义可知，行程时间可靠性实际上是行程时间的累积概率分布，求解路径、OD对行程时间可靠性的关键就是建立合理的行程时间概率分布模型.

1.1 路段行程时间可靠性

路段行程时间可靠性是指给定路段上的行程时间在可接受阈值内的概率.影响路段行程时间可靠性的因素主要是交通需求和路段通行能力两个方面.在交通需求不变的情况下，影响行程时间可靠性的主要因素是路段通行能力.各种因素将导致通行能力的变化，包括内生因素，如交通流量，不同车型的混合，交通事故等，以及外生因素如天气情况，道路施工维护等.由于路段通行能力是随机变化的，因此，路段行程时间也是随机变化的.定义路段行程时间是以流量为变量的阻抗函数，采用BPR函数表示，其形式为

式中：xa为路段a上的交通流量；Ca为路段a的通行能力为路段a的自由流行程时间；α和β为BPR函数的参数.

有学者将路段通行能力Ca用正态分布或者Beta分布表示，这里将路段通行能力Ca作为一个连续随机变量，分布函数为F（x），则路段a的行程时间可靠性为

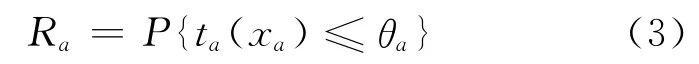
将式（2）代入式（3）得

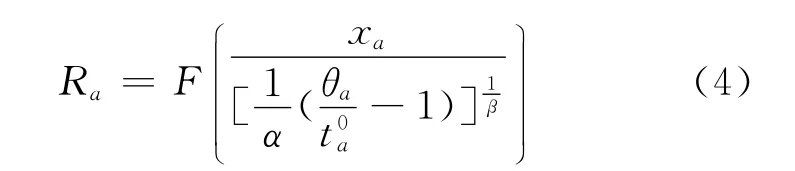
1.2 路径行程时间可靠性

路径行程时间可靠性是指给定路径上的行程时间在可接受阈值内的概率.路段行程时间可靠性可表示为

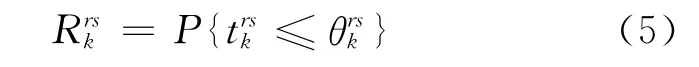
路段行程时间与路径行程时间有如下关系

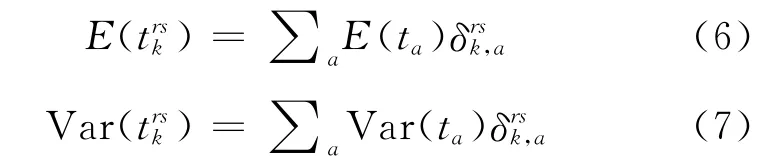
由于路径行程时间可靠性不能由组成该路径的各个路段的行程时间可靠性相加得来，同时路段时间的分布具有复杂性，直接计算路段行程时间可靠性不是那么轻而易举的.对于这种情况，Monte Carlo方法是一条行之有效的途径.

1.3 OD对行程时间可靠性

OD对行程时间可靠性是综合给定OD对之间所有被用户使用的路径的行程时间以得到一个关于OD对服务水平的测度.OD对之间各条路径组成的系统可以认为是一个并联的系统，则OD对行程时间可靠性可表示为

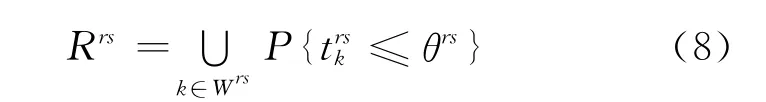
式中：θrs为OD对rs之间行程时间的阈值；Wrs为OD对rs之间所有路径的集合.

1.4 系统行程时间可靠性

系统行程时间可靠性是考虑所有OD对得到的整个系统服务水平的指标.系统行程时间可靠性与整个交通系统的出行需求模式相关，可表示为各OD对行程时间可靠性的加权和，即

式中：qrs为OD对rs之间的交通需求.

2 Monte Carlo方法

用Monte Carlo方法计算行程时间可靠性的基本步骤如下.

步骤0 确定平衡流量xa，各条路段的通行能力Ca的分布，以及路段、路径及OD对之间行程时间阈值，令n＝1，s＝0.

步骤1 对每一个路段随机产生通行能力的样本值C（n）a.

步骤3 判断.若满足条件Z（θ），则s＝s＋1.

步骤4 若n＜N，则n＝n＋1，返回步骤1.若n＝N，则计算路段、路径或者OD对的行程时间可靠性R≈.式中：N为预先设定的最大仿真次数.

在计算路段、路径或者OD对的行程时间可靠性时，判断条件Z（θ）具有不同的形式：

根据OD对行程时间可靠性可以计算得到系统行程时间可靠性指标.

行程时间可靠性计算的工作流程图见图1.

3 求解平衡流量

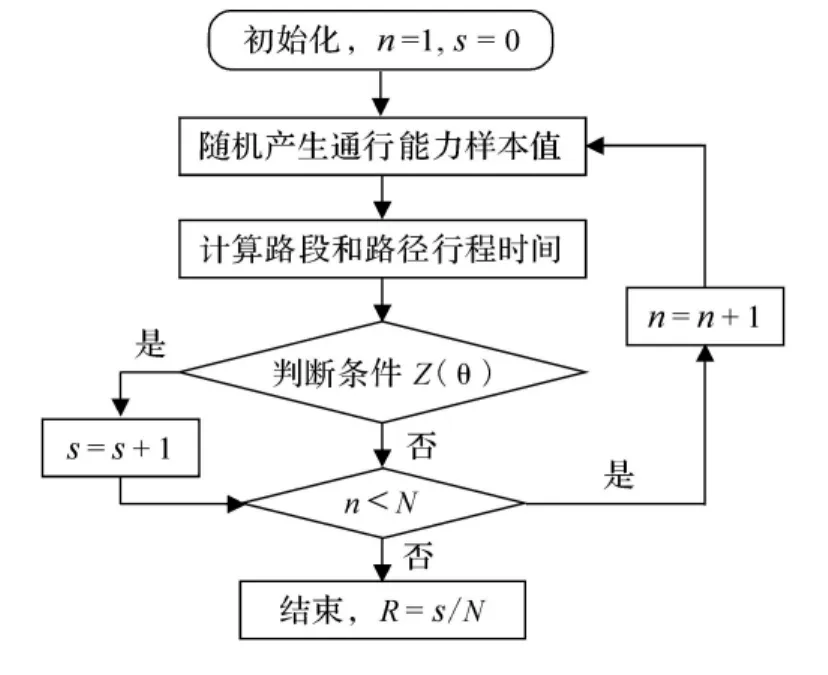
图1 行程时间可靠性计算流程图

在Monte Carlo方法求解行程时间可靠性的第一步中，需要先求解路网的平衡流量.在平衡流量分析中，需要考虑不确定状态下的路径选择行为.一般来说，在行程时间确定的情况下，出行者总是选择行程时间最短的路径，而在行程时间不确定的情况下，出行者选择rs之间路径k的概率为

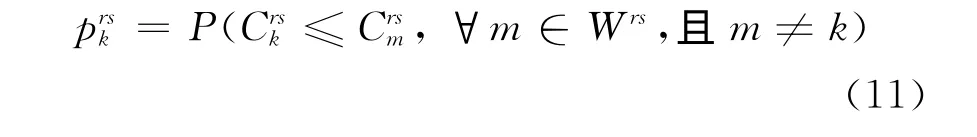
为实现基于行程时间可靠性的交通网络加载，现实可行而又有效的方法是Monte Carlo模拟.仿照Sheffi中随机网络加载的思路［10］，具体步骤如下.

步骤1 从Ca，a∈A的随机分布中随机抽取路段通行能力样本.更新路段行程时间＝.

式中：ε为预先设定的常数，表明对计算精度的要求.

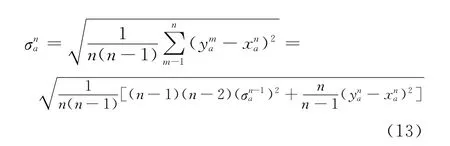
上述模拟方法的一个优点是不要求对路径行程时间进行抽样，因此，路径列出可以避免.此外，路段a流量估计的标准差，可以根据3个参数的值来计算，即和，不需要记录每次循环产生的，从而节约计算机内存.

4 算 例

如图2所示的测试网络，假设只有2个OD对，OD对（1→5）之间的交通量q15＝70辆／min，OD对（2→5）之间的交通量q25＝80辆／min.BPR函数中参数α＝0.15，β＝4.各路段的自由流行程时间和最大通行能力见表1.

图2 测试网络

建立路段通行能力的统计分布特性需要足够的统计数据，在缺乏相关数据的情况下，可用截尾正态分布、Beta分布或者均匀分布等来描述，一般来说，同一网络中的各个路段的通行能力分布特性也不尽相同.这里在不改变问题性质的前提下，假设路段通行能力在其最大通行能力和最大通行能力的1／2之间服从均匀分布.利用基于Monte Carlo模拟的加载算法求得各路段的平衡流量见表1.

取所有φi＝1.2，各路段和路径的行程时间可靠性分别见表2、表3.

OD对行程时间可靠性分别为R15＝0.154，R25＝0.440.最后可求出系统行程时间可靠性R＝0.307.

表1 路段自由流行程时间、最大通行能力和平衡流量

表2 路段行程时间可靠性

表3 路径行程时间可靠性

可靠性数值越大，表明该路段、路径、OD对或者整个系统应对日常变故的能力越强.此外，出行者可以根据路径行程时间可靠性，选择相对可靠的路径，制定相应的出行计划，保证在规定的时间内完成出行.

5 结束语

实际路网中，各种随机因素可能导致行程时间产生不确定性.行程时间可靠性作为这种不确定性的量度，不仅指示着路网的服务水平，而且会影响出行者的路径选择行为.本文从出行者的角度出发，提出了路段、路径、OD对以及系统行程时间可靠性的定量计算方法，给出了基于Monte Carlo仿真的行程时间可靠性的求解方法，计算结果具有明确的物理意义，出行者可以根据行程时间可靠性进行出行决策.

［1］ASAKURA Y，KASHIWADANI M.Road network reliability caused by daily fluctuation of traffic flow［C］／／Proceedings of 19th PTRC Summer Annual Meeting Brighton，1991：73－84.

［2］刘海旭，卜 雷，蒲 云.随机路网的行程时间可靠性［J］.土木工程学报，2004，37（8）：102－105.

［3］IIDA Y.Basic concepts and future directions of road network reliability analysis［J］.Journal of Advanced Transportation，1999，33（2）：125－134.

［4］CHEN A，CHOOTINAN P，ZHOU Z.Capacity reliability versus travel time reliability in the network design problem［C］／／The 3rd International Symposium on Transportation Network Reliability，the Netherlands，2007：152－160.

［5］ARROYO S，KORNHAUSER A.Modeling travel time distributions on a road network［C］／／Proceedings of the 84th Transportation Research Board Annual Meeting.Washington，2005：102－110.

［6］陈 琨，于 雷.基于对数正态和分布的路径行程时间可靠性模型［J］.北京交通大学学报，2009，33（3）：35－39.

［7］LO H K，TUNG Y K.Network with degradable links：capacity analysis and design［J］.Transportation research part B，2003，37：345－363.

［8］袁鹏程，韩 印，马万达.基于行程时间可靠性的随机交通网络均衡模型［J］.上海理工大学学报，2008，30（4）：352－356.

［9］陈建林，刘海旭，程学庆，等.基于行程时间可靠性的多类用户交通分配模型［J］.西南交通大学学报，2007，42（1）：115－119.

［10］SHEFFI Y.Urban transportation networks：equilibrium analysis with mathematical programming methods［M］.New Jersey：Prentice－Hall，Inc.，Englewood Cliffs，1985.