线性方程组迭代解法平均收敛速度收敛阶的定量估计

刘宇民

(太原师范学院数学系，山西太原030012)

在自然科学和工程技术中,很多问题的解决常常归结为求解线性代数方程组,迭代法就是用某种极限过程去逼近线性方程组精确解的方法,该方法具有对计算机的存贮单元需求少,程序计算简单,原始系数矩阵在计算过程中不变等优点,是求解大型稀疏矩阵方程组的重要方法。常用的迭代法有Jacobi迭代法、Gauss-seidel迭代法等。

1 迭代法原理和性质

1.1 Jacobi迭代原理

设有方程组

其中，A∈Rn×n，x，b∈Rn。

A为非奇异矩阵,可分裂为A＝D－L－U,其中:

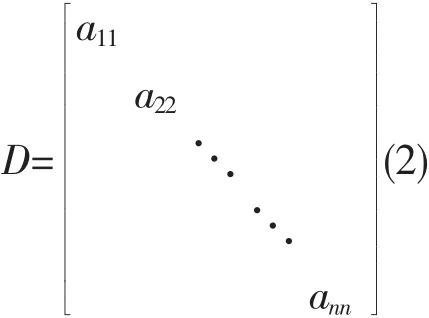
将式(1)用矩阵形式表示为

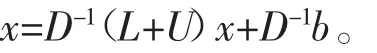
令

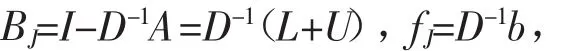
由此可构造迭代公式:

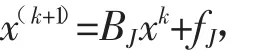
故迭代公式的形式为

这种方法称为Jacobi迭代法,其中BJ称为Jacobi迭代矩阵。

1.2 Gauss-Seidel迭代原理[1]

对式(1)中的系数矩阵A分裂为A＝D－L－U,其中D，L，U与式(2)相同。

将式(1)可写成矩阵形式Dx＝b＋Lx＋Ux，进而（D－L）x＝b＋Ux,若设（D－L）－1存在,则

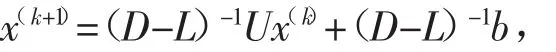
其中,BG＝（D－L）－1U,f＝（D－L）－1b，于是 Gauss-Seidel迭代公式的矩阵形式为

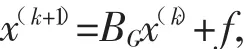
BG称为式(1)的Gauss-Seidel迭代法的迭代矩阵。

通过实例分析,我们可以得出:由于Gauss－Seidel迭代充分利用了迭代过程的新信息,一般来说,它的迭代效果要比Jacobi迭代好[1],当然也有例外的情形。文中讨论Gauss－Seidel和Jacobi迭代法的平均收敛速度与渐进收敛速度的关系。

1.3 这两种迭代方法收敛性与Bk→0是否成立有关，且敛速与Bk→0的速度有关[1]

当 ρ（B）＜1 时,Bk趋于零矩阵的速度有赖于 ρ（B）的大小:一般说来,ρ（B）愈小,则Bk趋于零矩阵的愈快,反之就愈慢。通常,当 ρ(B)＜1时,可以用正数－1nρ(B)的大小作为迭代法渐进收敛速度的度量。这时ρ（B）愈小,迭代法的收敛速度愈大。

1.4 平均收敛速度与渐进收敛速度之间的联系

对于收敛的迭代法xk＋1＝Bxk＋f（k＝0，1，2，…）,Rk＝－ln（‖Bk‖1/k） 称为平均收敛速度(它与所用的范数以及 k 有关);R∞＝－lnρ（B）称为渐进收敛速度。可以证明因此当k→∞时假设成立下列渐近关系式(常数),为估计平均收敛速度收敛到渐进收敛速度的阶,当k充分大时有如下近似形式:

两边取对数得:

此式说明当k较大时,lnRk＋1与lnRk有近似的线性关系,而它们的斜率刚好为p,这样可以通过当k较大时作出lnRk＋1与lnRk数据拟合曲线的方法估计出收敛阶p。

2 数值估计渐进收敛速度和平均收敛速度的关系

考虑五阶方程组

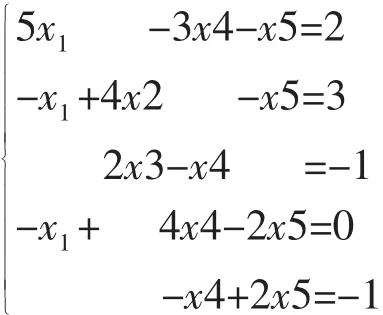
其Jacobi迭代法的迭代矩阵为

渐进收敛速度为:

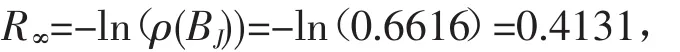
则迭代平均收敛速度Rk(见表1)以及取对数后作最小二乘拟合图像(见图1)如下所示:

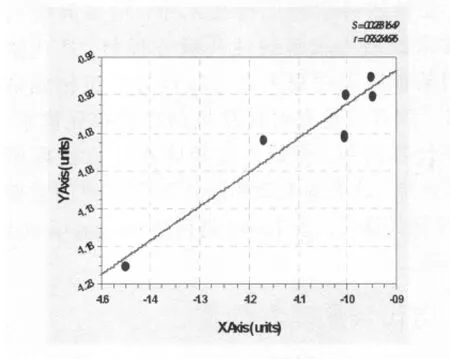
图1 最小二乘拟合图像

Linear Fit:y=a+bx Coefficient Data:

a＝－0.53486615 b＝0.4411919

即

ln（Rk＋1）＝ 0.4411919ln（Rk）－0.53486615，

其中，由(3)式定义的收敛阶 p＝0.4411919。而该方程组的Gauss－Seidel迭代矩阵为:

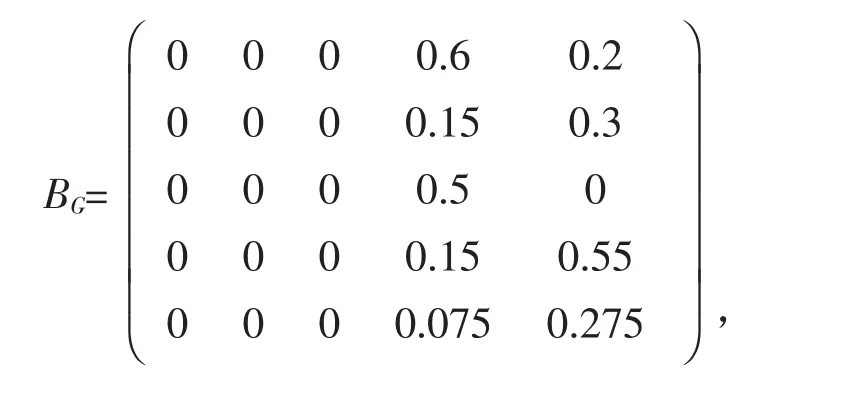
其渐进收敛速度为

R∞＝－ln（ρ(BG))＝－ln（0.425）＝0.855666，

则迭代平均收敛速度Rk(见表2)以及取对数后作最小二乘拟合图像(见图2)如下所示:

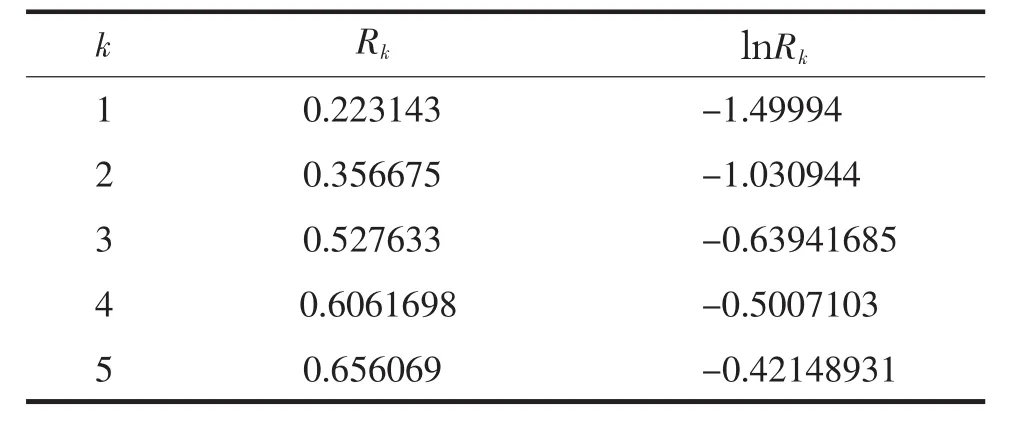
表1 迭代平均收敛速度Rk(以下Rk均在∞范数意义下得出)

表2 迭代平均收敛速度Rk(以下Rk均在∞范数下得出)

Linear Fit:y=a+bx Coefficient Data:a=-0.10426802 b=0.59261285

即

ln（Rk＋1）＝ 0.59261285ln（Rk）－0.10426802

从而得知由(3)式定义的收敛阶为 p＝0.59261285。

注:在本例中,由于方程组的系数矩阵严格对角占优,故前述两种迭代过程均收敛,依实际迭代过程:对 Jacobi迭代有‖x（34）－x（33）‖∞≤10－6‖x（33）‖∞而 Gauss-Seidel迭代有‖x（19）－x（18）‖∞≤10－6‖x（18）‖∞,即二者均收敛,但后者更快一些[1]。这与收敛阶p＝0.59261285＞0.4411919 之间关系一致。

图2 最小二乘拟合图像

[1]陈公宁,沈嘉骥.计算方法[M].北京:高等教育出版社,2002.

[2]蔡大用.数值分析与实验学习指导[M].4版.北京:清华大学出版社,2001.

[3]李庆扬,王能超,易大义.数值分析[M].武汉:华中科技大学出版社,2006.

[4]王兵团,桂文豪.数学实验基础[M].北京:北方交通大学出版社,2003.

[5]吴勃英.数值分析[M].北京:高等教育出版社,2007.

[6]赵秉新,郑来运.MATLAB在求解线性方程组的应用[J].通化师范学院学报,2007,28(12):13-15.

[7]宋道金,赵文玲.线性方程组的补充定理[J].淄博学院学报,2000,2(3):3-5.

[8]Richard L，Burden,Douglas J,et al.NUMERICAL ANALYSIS数值分析[M].北京:高等教育出版社，2005.