基于广义功率谱密度的分布压缩宽带频谱感知

赵春晖，腾志军，马 爽

（哈尔滨工程大学信息与通信工程学院，哈尔滨150001）

0 引 言

频谱感知（Spectrum sensing）技术包括匹配滤波器检测［1］、能量检测［2］和循环平稳特征检测［3］，也有基于以上技术的合作检测技术［4－5］。以上的频谱感知都是针对单个频带的感知，也就是通常所说的主用户信号检测，与之相应的还有宽带频谱感知［6］。频谱感知中的宽带频谱感知实质上是宽带频谱的估计，宽带感知为主用户信号检测提供了先验的频段知识，通过宽带频谱感知的结果，主用户信号检测能够有的放矢地进行。目前，宽带频谱感知的研究主要有以下两种：①借助硬件实现，具体就是在射频前端设置一组可调的窄带带通滤波器，宽带信号并行或者逐个通过滤波器组，进而完成宽带频谱的扫描。这种方法虽然能够实现宽带频谱感知，但是它需要增加大量的射频元件，大大增加了系统的硬件开销；②借助高速的数字信号处理技术，实现扫描较宽的频带。

目前广泛研究的宽带频谱感知都集中在高斯背景下，由于实际通信信道会存在非高斯噪声，如脉冲噪声，本文将研究在脉冲噪声背景下的宽带频谱感知。噪声的数学模型是Alpha稳定分布（即为高斯噪声的推广），既能描述不同特征指数的脉冲噪声又能描述高斯噪声。由于Alpha稳定噪声（特征值不为2时）不具有有限的二阶矩，因此通常的频谱估计都会受到Alpha稳定分布噪声的影响。本文根据Alpha稳定分布噪声的特点扩展了传统的功率谱密度的概念，提出基于分数低阶自相关的广义功率谱密度。另外，由于宽带频谱感知的接收信号带宽较宽，对于信号处理的硬件开销较大，本文借鉴文献［7-8］提出的压缩频谱感知方法，提出基于分数低阶自相关的分布压缩宽带频谱感知方法。

1 Alpha稳定分布噪声

Alpha稳定分布是高斯分布的推广，即高斯分布仅是它的一个特例。事实上，很多不满足经典的中心极限定理的数据都可以用稳定分布来描述，因此具有更普遍的应用范围。Alpha稳定分布与高斯分布的一个重要区别在于前者不具有α（α为特征指数）阶及以上各阶统计量［9］。

Alpha稳定分布Sα（γ，β，a）没有统一闭式的概率密度函数。通常用特征函数对其进行描述［10］：

式中：sgn（·）为符号函数，且

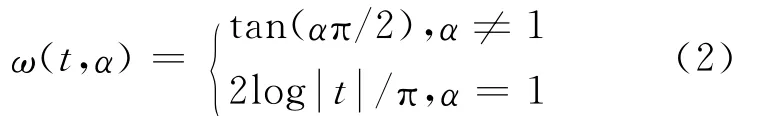
式中：0＜α≤2；－1≤β≤1；γ＞0；－∞＜a＜∞，稳定分布完全由4个参数α、β、γ、a来决定。其中，α为特征指数，用来度量分布函数拖尾的厚度，对于观测到的一个稳定随机变量，α值越小，表明其拖尾越厚，则偏离其中心值的样本越多。α＝2与高斯分布一致（对任意的β）。γ是比例参数，也称为分散系数，它与高斯分布的方差类似，在高斯分布情况下等于方差的一半。β是对称参数，β＝0时，稳定分布是关于a对称的。在这种情况下的分布称为对称α稳定分布或称为SαS。a是位置参数。

对于SαS分布噪声来说，由于不存在有限的二阶矩，致使噪声的方差变得没有意义，因此采用混合信噪比（MSNR），混合信噪比定义为

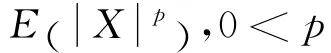
2 基于广义功率谱密度的分布压缩宽带频谱感知

2.1 基于分数低阶自相关的广义功率谱密度

当接收信号受到Alpha稳定噪声的影响时，一般的功率谱密度（PSD）将很难实现宽带频谱感知。由于Alpha稳定分布噪声不存在有限二阶矩，存在小于α的分数低阶矩，本文借鉴分数低阶矩的概念提出分数低阶自相关及广义功率谱密度（GPSD）的概念。本文假设接收信号为实信号。首先，分数低阶自相关函数定义为

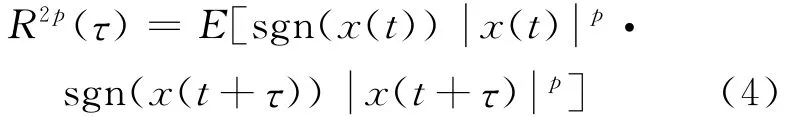
分数低阶自相关实际上是将信号的幅度进行分数低阶压缩，目的是抑制Alpha稳定分布噪声较大的幅度值。乘以符号函数是为了保证信号相位信息不变。进一步，根据功率谱密度与自相关函数的关系类推，广义功率谱密度可定义为

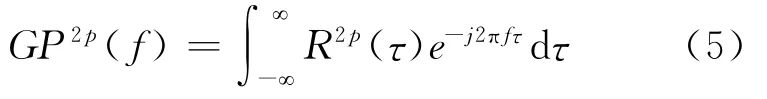
由于α≤2，2p＜α，即2p＜α≤2，所以，p≤1。当α＝2，p＝1时，

由以上两式可知，当α＝2，p＝1时，广义功率谱密度演变为传统的功率谱密度。因此，本文提出的广义功率谱密度的概念同样适用于高斯噪声。由于分数低阶矩充分抑制了Alpha稳定噪声的脉冲，因而，这种广义功率谱密度可以体现信号的频谱特性。

为了验证广义功率谱定义的有效性，图1给出了在Alpha稳定噪声背景下广义功率谱密度（GPSD）和传统功率谱密度（PSO）的试验比较结果。此时，混合信噪比MSNR＝0.8 d B。特征指数α＝1.5。由图1可知，在Alpha稳定分布噪声的影响下，传统的功率谱密度无法体现信号的频谱特性，而广义功率谱密度却能有效地抑制脉冲特性，能较好地体现信号的频谱特性。

图1 SαS噪声下GPSD与传统PSD的比较Fig.1 Comparison between GPSD and PSD in SαS noise

2.2 分布压缩宽带频谱感知

当认知用户接收宽带信号时，由于受到无线环境、地理位置等的影响，单个认知用户估计的宽带信号的功率谱密度有可能达不到满意的效果。为了更好地估计宽带频谱，引入合作机制，几个认知用户同时测量一段宽频信号，对所有合作用户的观测信息进行融合，最终得到宽带频谱的估计。由于宽带频谱感知的信号频带较宽，采样值个数将较多，因而多个认知用户联合估计PSD时将有大量的数据传输给融合中心才能实现最终的估计。本文借鉴压缩感知（Compressed sensing）理论，提出在Alpha稳定分布噪声下基于分数低阶自相关的分布压缩宽带频谱感知。原理框图如图2所示。

图2 基于分数低阶自相关的分布式压缩宽带频谱感知框图Fig.2 Distributed compressive wideband spectrum sensing based on fractional lower order autocorrelation

图2描述了Alpha稳定噪声下，基于分数低阶自相关的宽带频谱感知方案。J个认知用户接收同一频段内的信号，分别为x1（n），…，xJ（n）。由于频谱宽，采样值个数较多，接收信号分别进行分块处理［8］，每块数据长度为N×1。第j个认知用户的第k块数据可以表示为

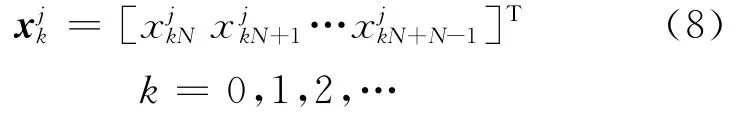
每块数据根据式（4）进行分数低阶处理，即

每个认知用户通过分数低阶处理过的数据分别计算2 N×1的分数低阶自相关函数向量：

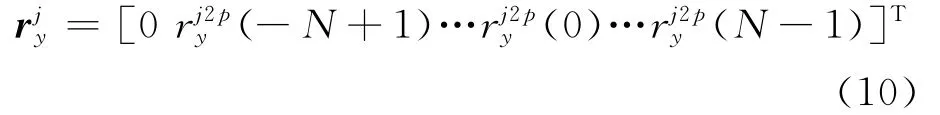
其中，分数低阶自相关函数向量的估计是由每段信号自相关的平均得到［8］。

根据压缩感知理论，分数低阶自相关函数向量具有可压缩性，并且，不同认知用户测量的分数低阶自相关函数之间具有联合稀疏特性。因此，可以借助分布式压缩重构原理压缩分数低阶自相关向量，再通过所有合作认知用户压缩后的分数低阶自相关向量联合重构分数低阶自相关向量，进而得到联合估计的广义功率谱密度。

压缩采样通过2 M×2 N的压缩矩阵ΦI实现，压缩测量后的分数低阶自相关向量＝ΦI，j∈｛1，2，…，J｝。压缩后的向量大小为2 M× 1，此时压缩比为M／N。根据压缩感知重构理论，分数低阶自相关向量的估计可以用式（11）描述。

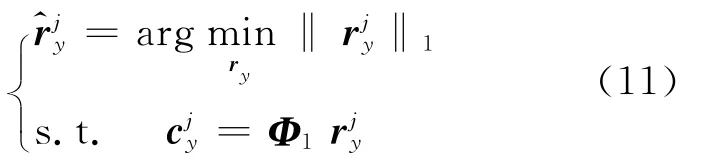
一般可以通过线性规划技术（如追踪算法或迭代贪婪等算法）解决式（11）。通过J个压缩重构的分数低阶自相关向量平均即可得到联合估计的分数低阶自相关向量：

分数低阶自相关的估计向量再经过傅里叶变换即可得到估计的广义功率谱密度：

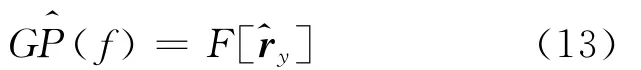
3 仿真性能分析

本节将讨论在Alpha稳定分布噪声下基于分数低阶自相关的宽带频谱感知性能。待测信号为DVB信号，频谱覆盖范围为0～4 MHz，三路信号宽带均为0.8 M，载频分别为1、2、3 MHz。背景噪声为Alpha稳定分布噪声。基于分布式压缩重构的广义PSD估计的评价性能指标为均方误差MSE，其定义为［8］

第一，在Alpha稳定分布噪声干扰下，其特征指数α＝1.5，单个认知用户处理宽带信号，先比较受到Alpha稳定分布噪声干扰信号的广义功率谱密度和传统功率谱密度，再比较不受干扰的纯信号的广义功率谱密度和传统功率谱密度。图3描述了在Alpha稳定分布噪声背景下，混合信噪比MSNR为0.8 d B时，受噪声干扰信号的广义功率谱密度与传统功率谱密度的仿真结果。图例中的“S”和“N”分别代表信号和噪声，为了验证广义功率谱密度是否能够描述原始无噪声信号的频谱特性，图3还特别描述了在无噪声干扰情况下的传统功率谱密度和广义功率谱密度。由图3可知，估计的GPSD能较好地体现信号的频谱特性。

第二，为了验证本文提出的广义功率谱密度适用于高斯噪声，设α＝2，比较加噪信号和原始信号的广义功率谱密度和传统功率谱密度。图4给出了仿真结果。由图4可知，对于受高斯噪声干扰的信号，使用广义功率谱密度和传统功率谱密度描述信号的频谱特性是一样的。因此，本文提出的广义功率谱密度的概念不但适合Alpha稳定分布噪声，而且同样适合高斯噪声。

图3 PSD和GPSD的比较（α＝1.5）Fig.3 Comparison between GPSD and PSD（α＝1.5）

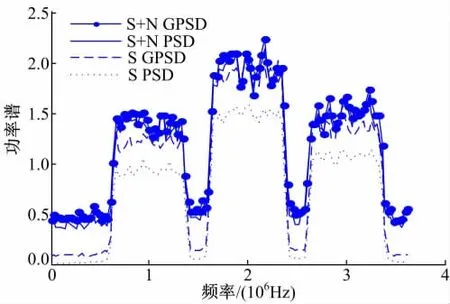
图4 PSD与GPSD的比较（α＝2）Fig.4 Comparison between GPSD and PSD（α＝2）

第三，为更好地描述宽带信号的频谱特性，本文提出了基于多用户合作的分别压缩宽带频谱感知。为了证明算法的有效性，设3个认知用户都接收到受Alpha稳定分布噪声干扰的宽带信号，但是它们接收信号的混合信噪比各不相同，将分数低阶自相关函数向量进行压缩融合后得到广义功率谱密度。图5描述了在Alpha稳定分布噪声背景下（α＝1.5），混合信噪比MSNR为0.8 dB，压缩率M／N＝0.3时估计的广义功率谱密度。为了证明估计的有效性，图5特别描述了原始宽带信号在无噪声干扰情况下的GPSD。由图5可知，估计的GPSD能较好地体现原始信号的频谱特性。

第四，在Alpha稳定分布噪声背景下（α＝1.5），比较广义功率谱密度的估计均方误差。图6描述了在混合信噪比（MSNR）为0.8 dB时，单个认知用户单独估计和3个认知用户合作估计的广义功率谱密度均方误差（MSE）与压缩率的关系曲线。由图6可知，合作估计的均方误差小于单独用户估计的均方误差，压缩比越大，估计均方误差越小。图7描述了M／N＝0.3时，均方误差MSE与混合信噪比MSNR的关系曲线。由图7可知，合作估计的均方误差小于单独估计的均方误差，但是在MSNR较小时，合作估计的优势不太明显。这是由于无论采用什么样的功率谱密度估计算法，功率谱密度估计的均方误差MSE都将存在，而且，信噪比越小，均方误差MSE将越大，功率谱密度估计性能受到信噪比的限制。对于本文提出的广义功率谱密度同样受到混合信噪比MSNR的限制，因此，在混合信噪比较低时，无论采用哪种估计算法都不能达到完全准确估计。以上两个实验可以证明合作的广义功率谱密度估计优于非合作广义功率谱密度估计。

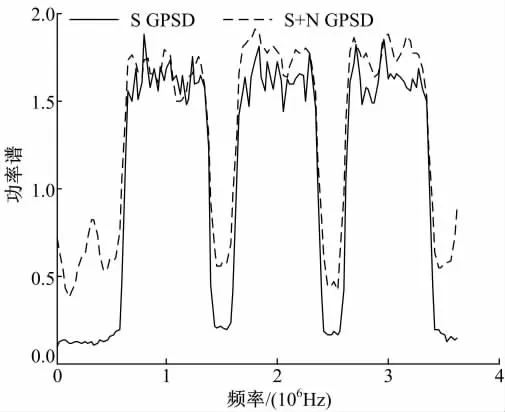
图5 MSNR＝0.8 dB，M／N＝0.3时估计GPSD与原始信号GPSD的比较Fig.5 Comparison of GPSD between estimated signal and original signal with MSNR＝0.8 dB，M／N＝0.3

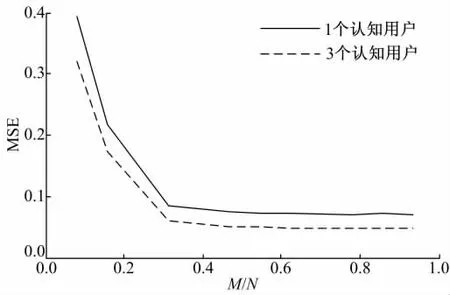
图6 MSE与压缩率的关系（平均MSNR＝0.8 dB）Fig.6 Relationship between MSE and compressed ratio

图7 MSE与MSNR的关系（M／N＝0.3）Fig.7 Relationship between MSE and MSNR

第五，为了研究基于合作的广义功率谱密度估计在不同压缩率及MSNR情况下性能的比较（α＝1.5），同时改变压缩率及MSNR时的均方误差性能如图8所示。由图8可知，MSNR越大，估计均方误差越小；压缩率越大，估计均方误差越小。当压缩率大于0.5以后，估计均方误差性能将很难提高，这是由于功率谱密度估计算法自身估计频谱的能力受到混合信噪比MSNR的限制所致。

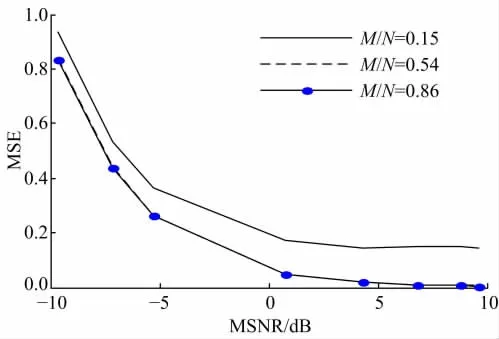
图8 合作估计MSE与MSNR的关系Fig.8 Relationship between MSE and MSNR under cooperation condition

第六，为了证明该算法适用于不同的噪声特征指数，图9描述了当α取不同值时，广义功率谱密度的均方误差与压缩率的关系。当α取不同值时，相应地，分数低阶指数P也要做适当的调整，依据Alpha稳定分布的特性及实验经验，本文取P≤α／4。由图9可知，α越小，估计的均方误差也越小，当α＝2时，噪声为高斯噪声，说明该方法在高斯背景下依然适用。

图9 不同α时MSE与压缩率的关系（平均MSNR＝0.8 dB）Fig.9 MSE vs compressed ratio with varyingα

4 结束语

由于在Alpha稳定分布噪声的影响下，传统的宽带频谱感知方法不再适用。本文提出基于分数低阶自相关的广义功率谱密度，又结合压缩感知理论，提出在Alpha稳定分布噪声下基于广义功率谱密度的分布式压缩宽带频谱感知方法。仿真结果表明，在Alpha稳定分布噪声下，基于分数低阶自相关的广义功率谱密度能有效地表达信号的频谱特性，能够完成宽带频谱感知。该方法对于高斯背景同样适用。另外，基于合作的宽带频谱感知优于非合作的宽带频谱感知。

［1］Chen X F，Nagaraj S.Entropy based spectrum sensing in cognitive radio［C］∥The 7th Annual Wireless Telecommunications Symposium，Ponoma，CA，U-nited States，2008：57-61.

［2］Cabric D，Mishra S M，Brodersen R W.Implementation issues in spectrum sensing for cognitive radios［C］∥Proc Asilomar Conf on Signals，Systems，and Computers，Pacific Grove，CA，United States，2004：772-776.

［3］Jarmo L，Visa K，Anu H，et al.Spectrum sensing in cognitive radios based on multiple cyclic frequencies［C］∥Proceedings of the 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications，CrownCom，Orlando，United States，2007：37-43.

［4］Renzo M D，Imbriglio L，Graziosi F，et al.Cooperative Spectrum Sensing for Cognitive Radios：Performance Analysis for Realistic System Setups and Channel Conditions［M］∥Mobile Lightweight Wireless Systems，Berlin，Springer，2009：125-134.

［5］Lunden J，Koivunen V，Huttunen A，et al.Collaborative cyclostationary spectrum sensing for cognitive radio systems［J］.IEEE Transactions on Signal Processing，2009，57（11）：4182-4195.

［6］Hu Z，Guo N，Qiu R.Wideband waveform optimization with energy detector receiver in cognitive radio［C］∥IEEE SoutheastCon 2010 Conference：Energizing Our Future，Charlotte-Concord，NC，United States，2010：198-203.

［7］Tian Z，Giannakis G B.Compressed sensing for wideband cognitive radios［C］∥IEEE International Conference on Acoustics，Speech and Signal Processing，Honolulu，HI，United States，2007：1357-1360.

［8］Polo Y L，Wang Y，Pandharipande A，et al.Compressive wide-band spectrum sensing［C］∥IEEE International Conference on Acoustics，Speech，and Signal Processing，Taipei，Taiwan，2009：2337-2340.

［9］Ma X Y，Chrysostomos L N.Joint estimation of time delay and frequency delay in impulsive noise using fractional lower order statistics［J］.IEEE Transactions on Signal Processing，1996，44（11）：2669-2687.

［10］吕铁军，郭双兵，肖先赐.调制信号的分形特征研究［J］.中国科学：E辑，2001，31（6）：508-513.

LüTie-jun，Guo Shuang-bing，Xiao Xian-ci.Research of fractal features of the modulated signal［J］. Science in China（Series E），2001，31（6）：508-513.