基于反馈增益反步法的非完整约束移动机器人路径跟踪控制

贾鹤鸣，宋文龙，陈子印

（1.东北林业大学机电工程学院，哈尔滨150040；2.哈尔滨工程大学自动化学院，哈尔滨150001）

0 引 言

轮式移动机器人结构简单，运动灵活、操作性能好、能量利用率高，已被广泛用于物流导引、家用清洁、智能导游和行星探测等领域［1］。轮式移动机器人是多输入多输出、欠驱动、本质非线性系统，而且具有非完整约束特性，这给实现精确路径跟踪控制带来了困难［2－3］。已有的控制方法大多采用动态反馈线性化方法和反步法［4－9］。用反馈线性化方法设计控制器时主要依赖于系统线性化部分，忽略非线性项对系统的影响，跟踪精度不高；而采用传统的反步法由于在设计过程中需要对虚拟控制量迭代求导，往往会令控制器结构复杂而不利于工程实现，难以保证实际工况下系统的控制品质。基于Serret-Frenet坐标系下的虚拟向导的跟踪方法通过引入额外的控制量，已经在移动机器人的路径跟踪控制中得到应用［10－11］。

本文针对轮式移动机器人的路径跟踪问题，提出了基于反馈增益的反步法设计控制器，借鉴了反步法通过迭代过程构造Lyapunov函数的优点，提出通过状态误差构造虚拟控制量的思想获得虚拟控制量，不同于传统的利用非线性项抵消的思想，克服了传统反步法在迭代过程中对虚拟控制量不断求导的缺点。通过控制器参数的设计消除了Lyapunov能量函数中部分符号不确定的非线性项，保证了系统的稳定性。采用本文方法进行了任意曲线的路径跟踪控制仿真实验，结果表明控制器表现出了较高的跟踪性能，可以实现对期望路径的精确跟踪。

1 问题描述

1.1 轮式移动机器人模型

对笛卡尔坐标系下的轮式移动机器人，其数学模型可以描述为

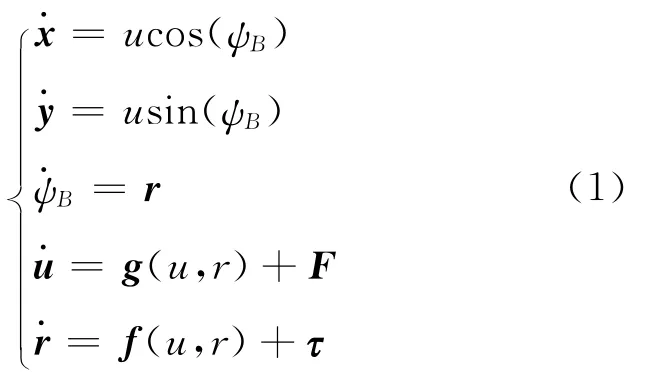
式中：x和y是大地坐标系下的相对位置；ψB是偏航角；u是体坐标系下轮式机器人的纵向速度；r是体坐标系下偏航角速度；F是纵向推力；τ是转向控制力矩；g（u，r）和f（u，r）表示模型中的非线性项。

在式（1）中，假设质心位于后轮轴的中点上，即车轮仅发生纯滚动而无侧向和纵向滑动，因此横向速度为零。本文假设轮式移动机器人仅能前向行驶，无法实现倒车行驶。

1.2 跟踪路径描述

跟踪路径Ω上的虚拟参考点P的坐标可以表示为某一标量参数μ∈R的函数，所以P点的位置坐标在固定坐标系下可表示为

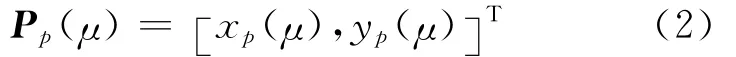
为了保证被跟踪曲线的光滑性，满足xp（μ）、yp（μ）连续可导。虚拟参考点的速度可以定义为

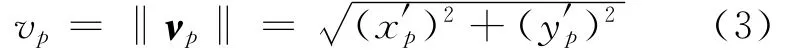
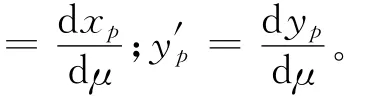
固定坐标系水平轴的夹角ψF定义为

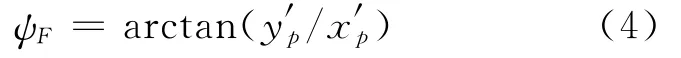
P点的旋转角速度ωF定义为

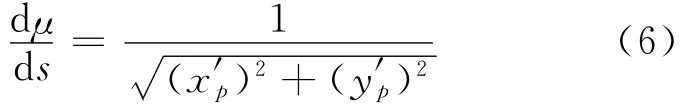
1.3 轮式移动机器人运动学误差方程

图1 轮式移动机器人路径跟踪示意图Fig.1 Schematic diagram of path following of wheeled mobile robot

如图1所示，P点为Q点在跟踪路径上的投影，以P为原点、由路径的切向量T和法向量N张成的坐标系为｛SF｝坐标系。P点在｛U｝坐标系下的速度表示为νP，坐标系 ｛U｝到坐标系｛SF｝的转换矩阵表示为RF，根据向量合成公式，Q点在｛U｝坐标系下的速度νQ可以表示为

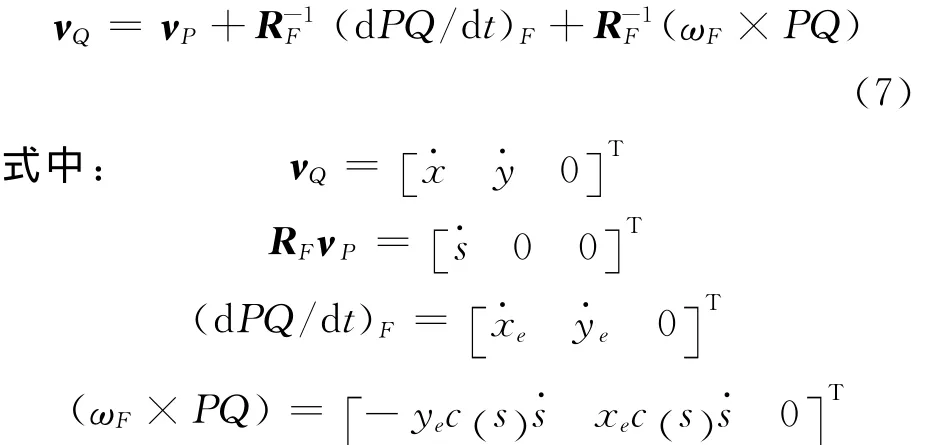
将上述变量代入式（7），得到由xe、ye、ψ构成的跟踪误差方程为

2 控制器设计

轮式移动机器人路径跟踪控制器的设计目的是满足跟踪误差方程（8）和动力学模型（1），对于给定连续光滑参考路径Ω和期望速度ud＞0，基于反馈增益思想的反步法设计路径上虚拟点的移动速率、轴向推力F和转向力矩Γ，使得跟踪误差xe、ye、ψ和u－ud渐进趋近于零。即满足－ud）＝0。

速度子系统由轴向推力F驱动，可作为单独的子系统控制，艏向和位置子系统通过迭代的方法进行控制。

2.1 速度子系统控制器设计

采用PD控制器对纵向速度u进行控制，使得u跟踪期望速度ud＞0，由式（1）的第4个方程可得移动机器人的虚拟纵向推力为

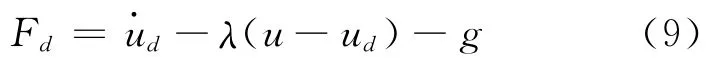
2.2 位置子系统控制器设计

采用基于反馈增益的反步法的思想设计位置跟踪控制器，由于横向运动无直接控制输入以及横向运动和转向运动的耦合作用，跟踪误差ye可以通过转向力矩调节，实现间接控制作用，首先定义控制误差变量和坐标变换为

式中：α1、α2分别为等价艏向角和艏向角速度虚拟控制量。

第一步：定义Lyapunov函数V1＝0.5z21，沿式（8）对等式两边求导得

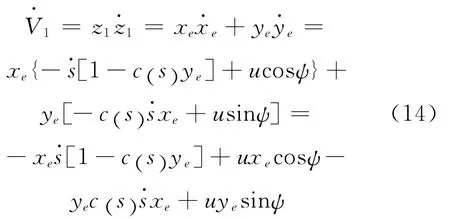
化简可得

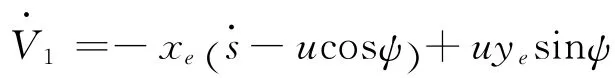
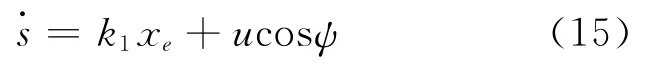
将式（15）代入式（14）得

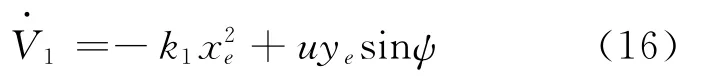
若取式（12）中的α1为

式（16）可以变形为

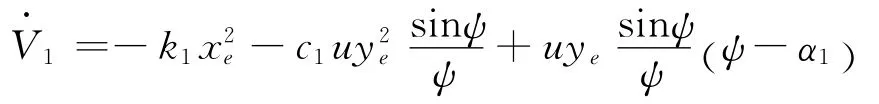
由式（12）和式（17）可得

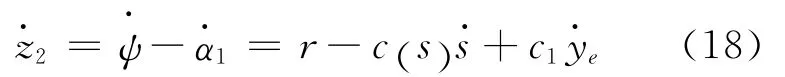
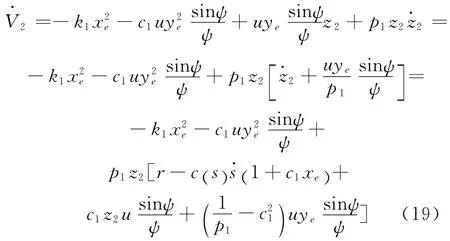
由上式可知，由于参数c1和p1均为控制器设计参数，不妨取p1＝1／c21，以消除式（19）中的非线性项，得到

若取式（13）中的虚拟控制量α2为

根据式（13）和式（21）可将式（20）化为

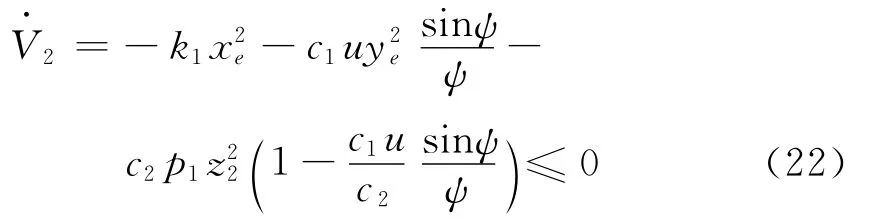
选择控制器参数c2，满足条件c2＞c1u。

由式（13）（21）可得

第三步：定义Lyapunov函数V3为

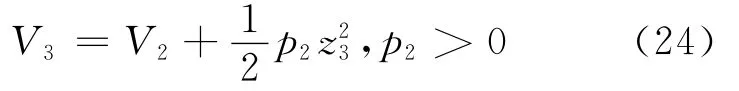
沿式（22）（23）求导得

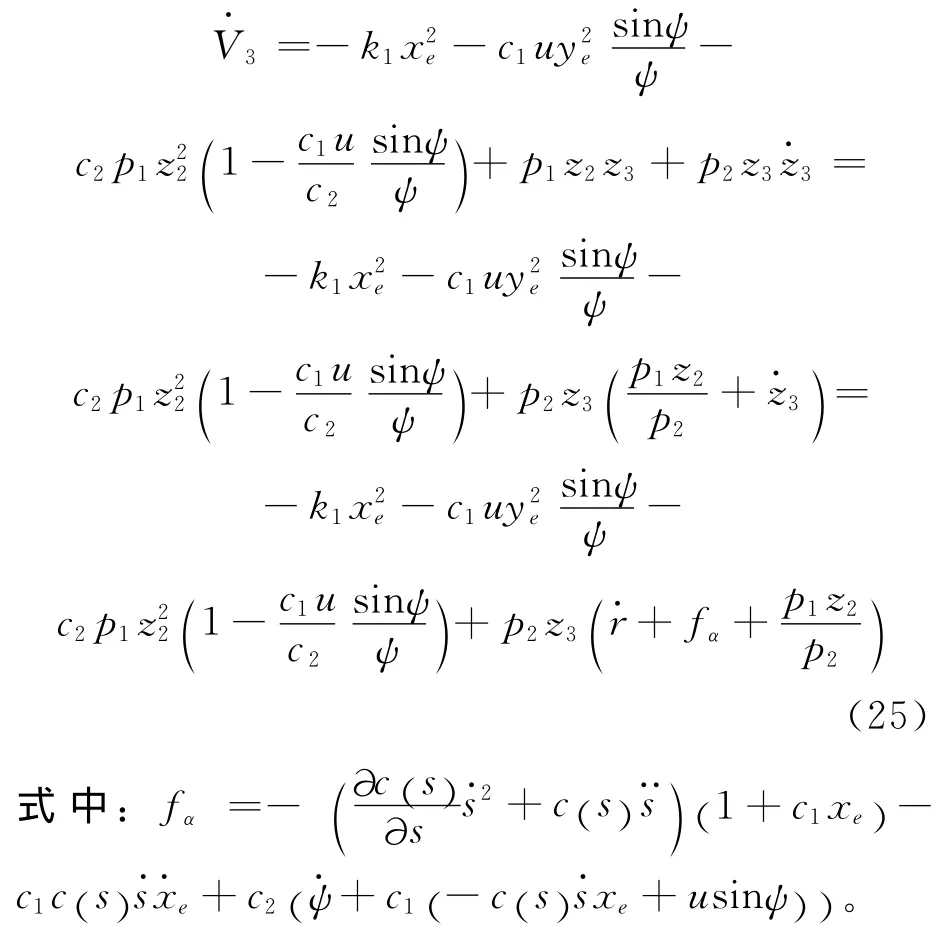
由此得到轮式移动机器人的路径跟踪等价控制输入为

如果上述控制器设计参数选取满足

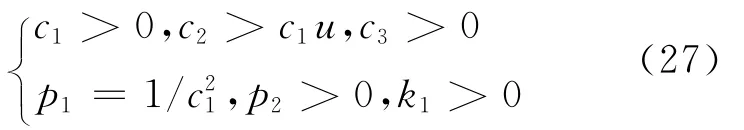
将式（26）代入式（25）得到

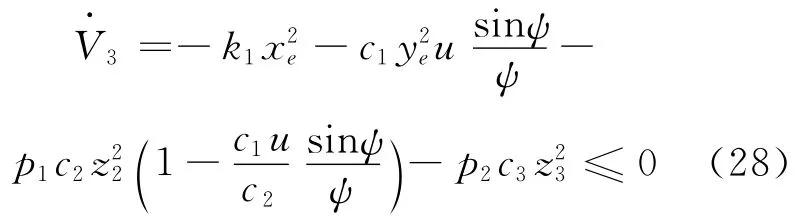
当且仅当（xe，ye，z2，z3）＝（0，0，0，0）时满足＝0，基于Lasalle不变性原理，通过合理地选择控制器设计参数c1、c2、c3、p1、p2和k1使得系统渐进稳定［12］。

3 仿真验证

仿真实验对象——轮式移动机器人的物理参数如下：质量为85 kg，长度为0.6 m，宽度为0.4 m。选取期望参数化跟踪路径为（单位为m）：

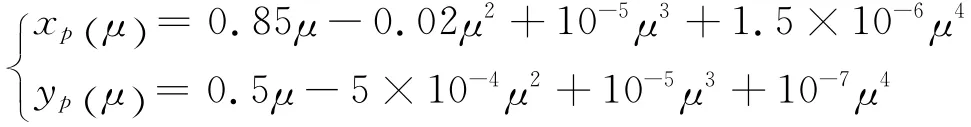
设轮式移动机器人的初始位置和姿态角为［x（0），y（0），ψ（0） ］＝ ［－18，－8，0］，初始速度和角速度为 ［u（0），r（0） ］＝［0，0］，期望速度ud＝1 m／s，取虚拟点的线速度增益参数k1＝0.6，其他控制器参数取值为：p1＝25，p2＝102，c1＝0.2，c2＝0.4，c3＝1。

图2 轮式移动机器人路径跟踪曲线Fig.2 Path following curves of wheeled mobile robot

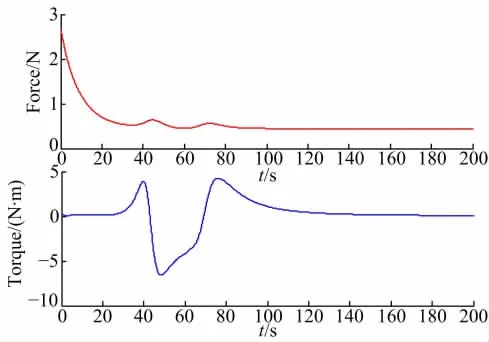
图3 控制输入量变化曲线Fig.3 Control variable curves

图2～图4为采用基于轮式机器人精确非线性模型且无外界扰动存在时的跟踪控制仿真结果。从图2中可看出，本文设计的控制器可以实现轮式移动机器人对期望路径的精确跟踪，具有较好的跟踪效果。图3为控制输入量的变化曲线，图4为路径跟踪误差的变化曲线。

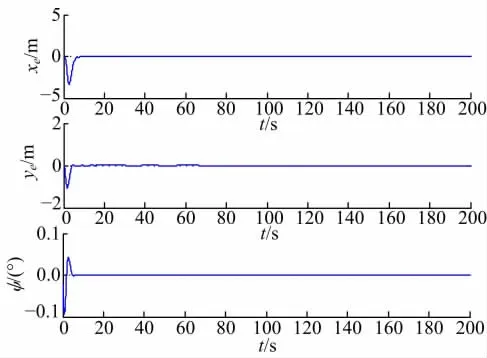
图4 路径跟踪误差变化曲线Fig.4 Path following error curves

4 结束语

针对非完整约束轮式移动机器人路径跟踪控制问题，结合Serret-Frenet坐标系，提出了基于反馈增益的Backstepping控制器设计思想，避免了反步法在迭代过程中存在虚拟控制量高阶导数的情况，得到的控制器形式依赖于状态误差和被跟踪路径参数，降低了控制器的复杂度，提高了控制器参数的可调节性。仿真结果表明设计的控制器可以实现对任意路径的精确跟踪，具有较好的工程实用价值。

［1］韩光信.控制受限的非完整轮式移动机器人运动控制研究［D］.长春：吉林大学通信工程学院，2009.

Han Guang-xin.Study on motion control for nonholonomic wheeled mobile robots with control input constraints［D］.Changchun：Jilin University，College of Communication Engineering，2009.

［2］马海涛.非完整轮式移动机器人的运动控制［D］.合肥：中国科学技术大学，2009.

Ma Hai-tao.The motion control of nonholonomic wheeled mobile robots［D］.Hefei：University of Science and Technology of China，2009.

［3］韩光信，陈虹，马苗苗，等.约束非完整移动机器人轨迹跟踪的非线性预测控制［J］.吉林大学学报：工学版，2009，39（1）：177-181.

Han Guang-xin，Chen Hong，Ma Miao-miao，et al. Nonlinear model predictive control of trajectory tracking for non-holonomic mobile robots with constraints［J］.Journal of Jilin University（Engineering and Technology Edition），2009，39（1）：177-181.

［4］Jiang Zhong－ping，Nijmeijer Henk.Tracking control of mobile robots：a case study in backstepping［J］. Automatica，1997，33（7）：1393-1399.

［5］Jiang Z P，Nijmeijer H.A recursive technique for tracking control of nonholonomic systems in chained form［J］.IEEE Transactions on Automatic Control，1999，44（2）：265-279.

［6］董文杰，霍伟.链式系统的轨迹跟踪控制［J］.自动化学报，2000，26（3）：310-316.

Dong Wen-jie，Huo Wei.Trajectory tracking control of chained systems［J］.Acta Automatica Sinica，2000，26（3）：310-316.

［7］Pourboghrat Farzad，Karlsson Mattias P.Adaptive control of dynamic mobile robots with nonholonomic constraints［J］.Computer and Electrical Engineering，2002，28（1）：241-253.

［8］Oriolo G，de Luca A，Vendittelli M.WMR control via dynamic feedback linearization：design，implementation，and experimental validation［J］.IEEE Transactions on Control System Technology，2002，10（6）：835-852.

［9］方浩，窦丽华，陈杰.轮式移动机器人滑移量重建与滑移补偿控制［J］.控制与决策，2010，25（5）：701-705.

Fang Hao，Dou Li-hua，Chen Jie.Sliding reconstruction and anti-sliding control of wheeled mobile robots［J］.Control and Decision，2010，25（5）：701-705.

［10］Casalino G，Aicardi M，Bicchi A，et al.Closed loop steering and path-following for unicycle-like vehicles：a simple lyapunov function based approach［J］. IEEE Robotics and Automation Magazine，1995，2（1）：27-35.

［11］Micaelli A，Samson C.Trajectory tracking for unicycle-type and two-steering wheels mobile robots［R］.Technical Report No 2097，INRIA，Sophia-Antipolis，France，1993.

［12］Li Zhen，Jing Sun，Soryeok Oh.Design，analysis and experimental validation of a robust nonlinear path following controller for marine surface vessels［J］.Automatica，2009，45（7）：1649-1658.