吸附-扩散模型应用研究

王一鸣

(中国联合工程公司，浙江 杭州 310022)

在反渗透工艺过程设计中，常用分离模型预测系统或元件的产水量和脱盐率。目前，工程上常用的分离模型有溶解-扩散模型[1]（SDM）和优先吸附-毛细孔流模型[2]（PSCFM）。随着人类对膜分离过程认识的不断深入，优化现有模型、建立新模型等研究成果不断涌现，其中一种新的描述多孔膜分离过程的模型——吸附-扩散模型[3~5]（ADM），引起了人们的兴趣。程会文等[6]以吸附-扩散模型（ADM）为理论基础，采用遗传算法对反渗透膜性能进行数学模拟，计算出了膜-溶质相互作用的物化参数。郭宇彬等[7]研究了吸附-扩散模型（ADM）与溶解-扩散模型（SDM）的相互关系，验证了吸附-扩散模型（ADM）的正确性。本文对吸附-扩散模型（ADM）进行数学简化，并利用简化模型对膜分离过程进行模拟。

1 吸附-扩散模型（ADM）

模型假设稳态时膜中溶液体积通量恒定，溶质、溶剂在膜表面和膜孔壁表面单分子吸附、脱附导致的扩散和膜孔内溶液相中溶质、溶剂的扩散共同构成了膜内物质的迁移，其溶质脱除率方程和溶液渗透通量方程为：

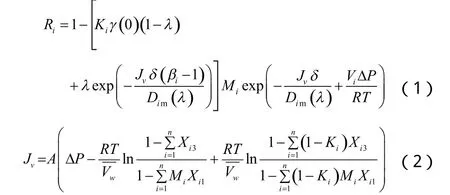
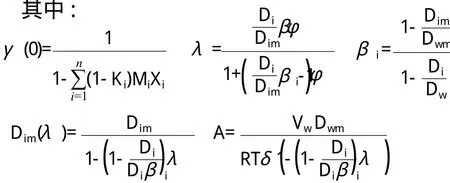
其中γ （0）是与膜电荷密度Xq有关的参数，λ是与膜孔隙率φ有关的参数，Ki为溶质组分i的分配系数，浓差极化比Ki(λ)为溶质组分i的表观分配系数，Ki(λ)=Kiγ(0)(1-λ)+λ。

由于吸附-扩散模型（ADM）数学形式比较复杂，当溶质摩尔分数较小时，对其进行一级近似处理，得：

2 模拟与分析

采用文献[8]的相关数据，分别用简化的吸附-扩散模型（ADM）和溶解-扩散模型（SDM）对KCl溶液反渗透过程进行模拟，见图1、表1和表2，分析可知：

（1） 吸附-扩散模型（ADM）较之溶解-扩散模型（SDM）能较好地描述KCl溶液反渗透过程。由式（3）、式（4）知，溶质脱除率、溶液渗透通量随操作压力的增大而上升。随着渗透通量的增大，浓差极化影响逐渐显现，溶质脱除率的上升幅度减小。

（2） 由Langmuir吸附等温式可知，溶质组分i在膜表面和膜孔壁表面吸附量随溶液浓度增大而增大，其分配系数Ki增大，而膜孔隙率φ则随溶质吸附量的增大而减小，吸附-扩散模型（ADM）中参数λ变小。因此，随着溶液浓度增大，溶质表观分配系数Ki(λ)增大，溶液渗透系数A减小。

图1 KCl溶液反渗透脱除率、渗透通量实验值与两种模型计算值随操作压力的变化关系

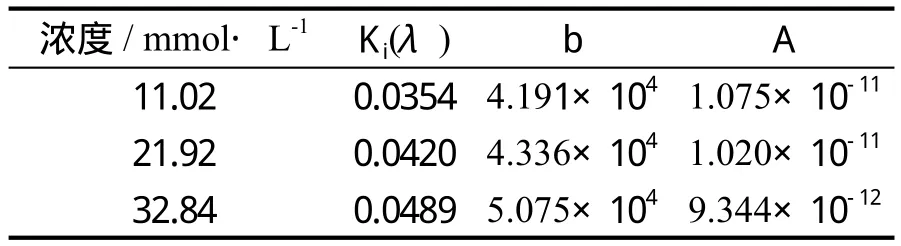
表1 吸附-扩散模型（ADM）拟合的参数值

表2 2种模型拟合的均方差

由于吸附-扩散模型（ADM）能够描述多孔膜的分离过程，故采用文献[9]的相关数据，用简化的吸附-扩散模型（ADM）对络合醋酸铅溶液超滤过程进行模拟，见图2、表3，可以看出简化的吸附-扩散模型（ADM）的计算结果与实验结果符合较好，随着溶液浓度增大，溶质表观分配系数Ki(λ)增大，溶液渗透系数A减小。

图2 络合醋酸铅溶液超滤过程脱除率、渗透通量实验值与模型计算值随操作压力的变化关系

表3 吸附-扩散模型(ADM)模拟超滤过程的参数值及均方差

3 结论

通过对吸附-扩散模型（ADM）溶质脱除率方程和溶液渗透通量方程进行一级近似处理，得到简化的吸附-扩散模型（ADM），利用简化模型对KCl溶液反渗透过程进行模拟，其拟合精度优于溶解-扩散模型（SDM），模型亦能较好地预测络合醋酸铅溶液超滤过程溶质组分脱除率和溶液渗透通量。简化的吸附-扩散模型（ADM）参数的变化能够直观地反映膜分离规律，随着溶液浓度增大，溶质表观分配系数Ki(λ)增大，溶液渗透系数A减小。该模型对膜分离工艺过程设计具有指导作用。

符号说明：

A： 溶液渗透系数，m3·m-2·s-1·Pa-1

Di，Dim： 分别为溶质组分i在溶液相和膜相中的扩散系数，m2·s-1

Dw，Dwm： 分别为溶剂w在溶液相和膜相中的扩散系数，m2·s-1

Jv： 溶液渗透体积通量，L·m-2·h-1

Ki： 溶质组分i在膜相和溶液相中的分配系数ki： 溶质组分i的传质系数，m·s-1

Mi： 溶质组分i的浓差极化比

Pi： 溶质组分i的透过率

Ri： 溶质组分i的脱除率

R： 气体常数，J·mol-1·K-1

T： 热力学温度，K

Vi： 溶质组分 i的偏摩尔体积，m3·mol-1

Ф： 膜的孔隙率

δ： 膜分离皮层厚度，m

γ（0）： 参数

βi： 参数

λ： 参数

b： 参数

σRi、σJv： 溶质脱除率、溶液渗透通量拟合均方差下脚标1、3：溶液侧、渗透侧

[1] Wijmans J G.，Baker R W. The solution-diffusion model：A review[J]. J Membr Sci，1995，107（1）：1-21.

[2] Sourirajan S. The mechanism of demineralization of aqueous sodium chloride solutions by flow，under pressure，through porous membranes[J]. Ind Eng Chem Fundam，1963，2（1）：51-55.

[3] 姬朝青. 反渗透溶质脱除率方程[J]. 化工学报，1994，45（3）：366-370.

[4] 姬朝青，陈浩. 反渗透、纳滤过程的物理化学研究(Ⅰ)[J]. 化工学报，2006，57（3）：601-606.

[5] 姬朝青. 反渗透、纳滤过程的物理化学研究(Ⅱ)多孔荷电膜的溶质分离规律[J]. 化工学报，2008，59（3）：615-623.

[6] 程会文，姬朝青，许力. 基于吸附-扩散模型和遗传算法的反渗透膜性能预测[J]. 化工学报，2007，58（8）：2027-2032.

[7] 郭宇彬，许振良，姬朝青. 吸附-扩散模型与溶解-扩散模型及其修正模型的相互关系[J]. 膜科学与技术，2010，30（2）：29-32.

[8] 王一鸣. 吸附-扩散模型一级近似式及其应用[J]. 能源工程，2010，（6）：45-47.

[9] 张永锋，云继征，包峰松，等. 膜传质的统计力学模型研究[J]. 内蒙古工业大学学报，2007，26（2）：87-92.