含表面缺陷的压力容器疲劳寿命数值模拟
金长义,陈金梅
(广西工业职业技术学院,广西 南宁 530003)
压力容器在制造、焊接和使用过程中常存在微观裂纹或宏观裂纹,在疲劳载荷的作用下扩展导致断裂失效破坏,最终导致灾难性事故的发生[1~2]。加上大部分压力容器都是在高温、高压、强腐蚀、易燃、易爆的工况条件下运行,因此对带缺陷的压力容器进行疲劳寿命估算是很重要的。
目前多采用确定性的疲劳断裂力学方法估算压力容器的疲劳寿命。但压力容器材料的机械性能、工况载荷、缺陷尺寸等因素都存在着随机性和不确定性,理论方法求得的结果不能准确地反映实际情况[3]。本文以概率论为基础,用疲劳断裂力学方法和蒙特卡罗模拟法对换热器的疲劳寿命进行可靠性估算。
1 基本理论
1.1 寿命计算
在恒幅疲劳载荷作用下,裂纹疲劳扩展速率可用Paris公式表示为:
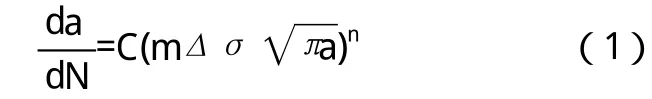
裂纹扩展寿命(剩余寿命)为:

其中:Δσ -应力变化幅值;
a0, ac-分别为初始裂纹尺寸和临界裂纹尺寸;
m-裂纹几何形状因子;
C,n-均为材料常数。
1.2 蒙特卡罗模拟法的随机抽样模型
蒙特卡罗(Monte- Carlo)法也称为随机模拟法、统计试验法等,它是目前在很多领域已经得到广泛应用的风险分析方法。它的基本思想是:若已知状态变量的概率分布,根据状态函数,利用蒙特卡罗模拟法产生符合状态变量分布的一组随机数,以之代入状态函数计算出状态函数的一个随机数。如此用同样的方法可产生N个状态函数的随机数[4]。
正态分布密度函数为:

对数正态分布密度函数为:

设η1η2成为[0,1]上均匀分布的随机变量,对于标准正态分布N(0,1),利用二元函数变换可得随机变量抽样值:

1.3 在给定可靠度和置信度下的剩余寿命
经过大量研究后可知,初始裂纹尺寸a0,应力变化幅值Δσ及系数C均服从对数正态分布,由式(2)积分可知寿命N 也服从对数正态分布。于是,破坏概率为p的剩余寿命的计算公式为[5]:

如果考虑置信度,破坏概率为p,置信度为r时疲劳寿命的χp(r)为:χp(r)=χ +κS,式中κ为单侧容限系数。
1.4 计算机编程
利用以上的理论计算机编程的程序流程图如图1所示。

图1 计算流程图
2 算例
某换热器承压体用7079-Tb铝合金制作,内径D=508mm,壁厚t=25.4mm,正常工作压力循环P= 0~21MPa,室温下材料的σs=457MPa,KIC=内壁沿母线方向发现半椭圆表面裂纹(a∶2C= 1∶4),现在计算这台换热器的剩余寿命(疲劳寿命)[6]。已知条件见表1。

表1 基本随机变量Table.1 Basic random variables
解:由程序计算得:当a0=1.0mm时,可靠度为99.9%时的疲劳寿命为16619循环;可靠度为99.9%置信度为90%时,疲劳寿命为10834循环。
不同初始裂纹尺寸下疲劳寿命曲线如图2所示。不同断裂韧性下疲劳寿命曲线如图3所示。可靠度和失效概率曲线如图4、图5所示。

图2 不同初始裂纹尺寸的疲劳寿命曲线

图3 不同断裂韧性下疲劳寿命曲线

图4 可靠度曲线
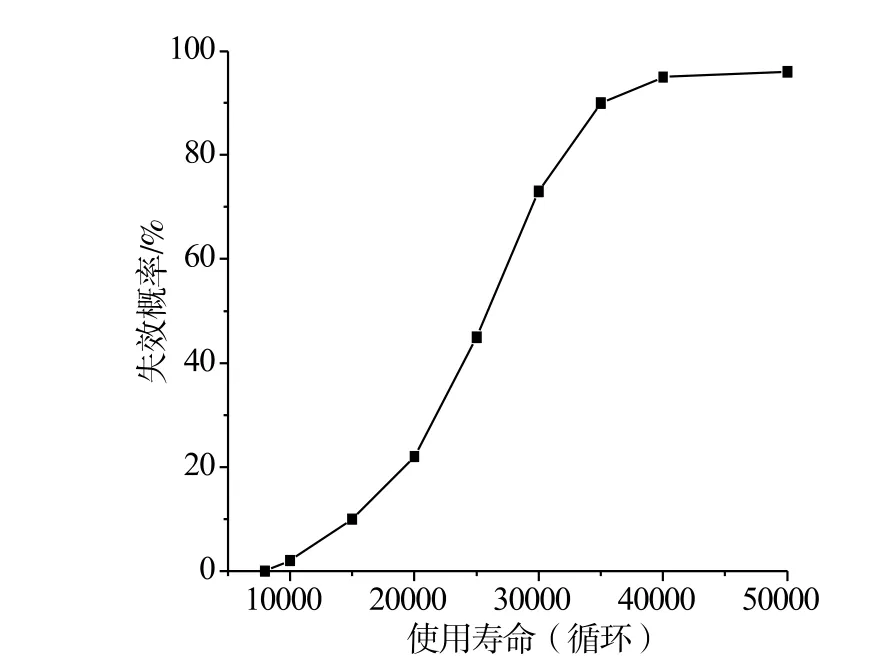
图5 失效概率曲线
3 分析讨论
(1)由图1可知,在相同初始裂纹尺寸下,可靠度和置信度下求得的疲劳寿命相差不多;而且随着初始裂纹尺寸的增加,疲劳寿命随之减小。
(2)随着断裂韧KC值的增大,疲劳寿命之增大;当KC=350时,疲劳寿命趋于零(图2)。
[1] 杨国军.压力容器焊缝及其附近微裂纹的检测[J].制造业自动化,2010,32(12):17-22.
[2] 金志江,韩树新.基于循环J积分的压力容器疲劳寿命预测的数值模拟[J].机械工程学报,2007,43(10):191-195.
[3] 马宇山,金涛.基于ANSYS的塔设备地震与风载分析[J].制造业自动化,2010,32(1):1-5.
[4] 陈群,孙磊.蒙特卡洛法在投标报价中的应用[J].武汉理工大学学报(信息与管理工程版),2009,31(3):503-506.
[5] 张伟,崔维成,查子初,王志群.厚壁筒结构疲劳寿命的可靠性分析[J].工程力学,1996,13(4):59-68.
[6] 孙奉仲.换热器的可靠性与故障分析导论[M].北京:中国标准出版社,1998.248-250.

