基于CAIV的导弹低成本保障性指标论证技术

刘 芳，赵建印，宋贵宝，刘 铁

（海军航空工程学院飞行器工程系，山东 烟台 264001）

导弹是现代高技术局部战争中消耗最多的高技术武器。导弹低成本问题是各国军方关注的一个焦点。目前，可用于导弹武器寿命周期费用管理的技术有很多，如费效分析、按费用设计(Design to Cost，DTC)、以费用为独立变量(Cost as an Independent Variable，CAIV)等[1]。国内对指标方案与费用的决策仍停留在传统的费效分析思想[2]，在权衡研究方面仍偏重DTC方法的研究[3-4]，同时对可靠性、维修性等保障性参数与费用的权衡也有一些研究[5-8]；国外的相关研究则主要是以CAIV 思想为主[9-10]。CAIV方法是20世纪90年代美国军方提出的一项武器装备采办费用管理技术[11]。CAIV 中最重要的概念是“独立变量”，认为费用与性能、保障性有同等的重要性，是设计的重要目标之一。与DTC方法相比，CAIV方法有了很大不同，CAIV 更加注重寿命周期费用和总拥有费用，而DTC 主要关心装备的研制与采购费用；CAIV 主要的需求是装备的作战能力，而DTC 则是装备的战术技术指标。CAIV 充分借鉴了以往的各种费用管理方法，如费用效能分析、基线费用估计(Baseline Cost Estimate)、DTC、寿命周期费用分析、价值工程等传统的技术经济分析方法。从这个角度上看，CAIV可以说是以前各种费用管理技术的综合集成[12-15]。

为了实现导弹低成本化目标，必须从指标论证入手，利用科学合理论证技术，综合考虑保障性指标、费用和作战效能三者之间的关系并进行权衡优化，从而为提出低成本保障性要求提供科学依据。传统装备保障性指标论证[15]中只将费用作为一个次要因素来考虑，使得研制出来的装备寿命周期费用较高。本文以反舰导弹论证为背景，在借鉴CAIV思想的基础上，结合反舰导弹的作战任务和使用保障特点，研究导弹武器低成本保障性指标论证设计技术，从而论证出寿命费用最少且易于保障的导弹武器系统。

1 CAIV 基本原理

在武器装备系统指标论证过程中，CAIV技术首先分别建立系统效能模型和费用模型，然后将两个模型综合起来，并结合各性能参数的取值范围，建立权衡模型，最终找出最佳平衡点。

1.1 作战效能模型

CAIV 作战效能模型的主要目的是用系统的主要的性能度量值(Measure of Performance，MOP)来描述系统的作战效能，即效能度量值(Measure of Effectiveness，MOE)。以关键MOP为参数描述的作战效能模型可以表示为：

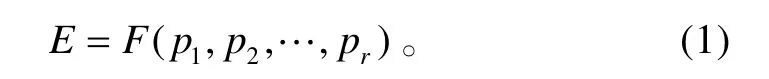
式(1)中：E为MOE；pi(i=1,2,…,r)为关键MOP。

影响导弹武器装备作战效能的因素主要包括两大类：一类是系统的固有能力，即性能设计参数；另一类则是保障性参数，又可分为综合参数、设计特性参数、保障资源参数3类。

在上述模型中，根据现有的技术水平和作战的需要，MOP和MOE都有一定的取值范围。设某MOP为pi，设其取值下限为piL，取值上限为pUi，则其取值范围为≤pi≤piU，可以通过分析导弹武器系统作战使命、目标特性、环境条件、现有技术水平、系统结构等各个方面，给出相对合理的指标取值范围。由于作战效能度量值，往往是越大越好，因此要规定其下限，即 E ≥ E*，E*为效能值或能满足作战需要的最低效能极限值。

1.2 费用模型

CAIV方法在装备立项论证和方案决策阶段所用的费用建模方法是参数费用估算法[11]。这是因为参数估算法在项目的早期是最为适用的费用估算法，虽然是一种比较粗略的估算方法，但能够满足系统顶层设计和指标论证的需要；同时它可以将设计变量作为影响费用的主要因素建立关系函数，正好满足权衡的需要。此外，参数估算模型往往是根据历史数据的回归分析而得到的，其中人的主观判断影响较少，属于比较客观的一种估算方法。

CAIV 费用模型以总拥有费用(Total Ownership Cost，TOC)来代替寿命周期费用，将每一个MOP都看作是影响费用的因素，通过费用分解结构(Cost Breakdown Structure，CBS)将系统的TOC 进行分解，其每一个费用单元都可通过MOP 进行描述。通过参数估算法，可以建立各费用单元与相应的MOP之间的函数关系：

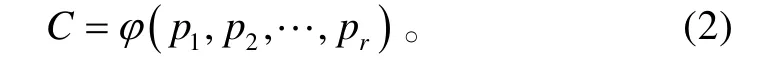
式(2)中：C为TOC；pi(i=1,2,…,r)为关键MOP。

在上述费用模型中，各费用单元也是存在约束条件的。在建模前，必须依据“经济可承受性”原则提出项目的费用预算，该预算是系统总拥有费用的上限，记为CU，则C≤CU；根据新研导弹装备特点，可对每个性能度量值对应的费用单元的费用上限进行界定，即 Ci≤CiU；必要时，还可设定费用的下限。

1.3 权衡优化模型

根据上述两个模型中所给出的MOP、MOE和TOC的取值范围和限制，可以得到如图1所示CAIV“权衡空间”，该“空间”实际上就是MOP指标论证方案的可行域。

CAIV 利用上述建模过程，通过系统关键性能参数，MOP 将系统的作战效能MOE与总拥有费用TOC 联系起来。建模完成后，将效能模型和费用模型联立起来，以“权衡空间(Trade Space)”作为约束条件，在确定了优化目标的基础上就可以进行权衡优化。优化设计的目标是使效能与费用达到一个令人满意的平衡点，于是就存在两种权衡优化模型。

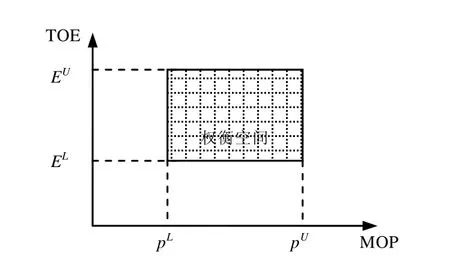
图1 权衡空间

模型I：在满足费用约束的条件下，使系统的效能达到最大。其优化问题可以描述为如下数学规划问题：

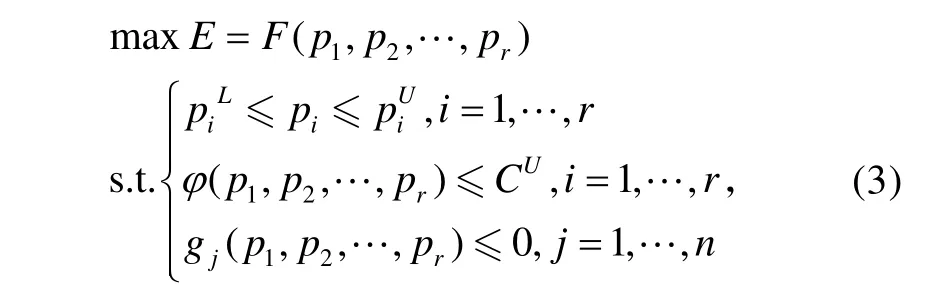
式中，gj(p1,p2,…,pr)为其他可能的约束条件。

模型II：在满足作战需求的情况下，使系统的TOC 达到最小。其优化问题可以描述为如下数学规划问题：

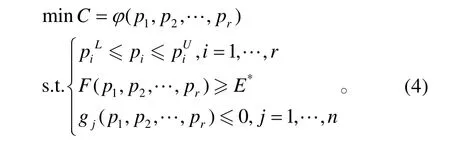
通过以上权衡模型，可以求得在权衡空间以内的最佳平衡点或最优解，即作战效能最大或总拥有费用最低的各关键性能参数指标方案。这些数据将为系统方案的决策以及之后的详细设计和工程研制提供依据。

2 模型应用研究

2.1 新型反舰导弹作战效能模型

美军在研究通用导弹系统时，用“发射一定数量的导弹摧毁目标的概率”作为衡量破坏力的效能度量指标。本文也采用类似方式来衡量反舰导弹的作战效能，它的基本定义是：n发导弹在同一条件下向同一目标发射，至少有一发杀伤目标的概率，记作 W (n)，

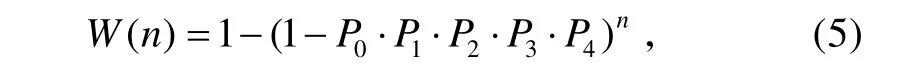
式中：P0为对抗敌方袭击概率；P1为在P0=1条件下武器系统的战备完好性指标；P2为在P0⋅P1=1条件下任务成功概率；P3为在P0⋅P1⋅P2=1条件下导弹反拦截概率，即突防概率；P4为在P0⋅P1⋅P2⋅P3=1条件下，单发导弹杀伤目标概率，它与弹头威力、落点精度、目标性质有关；n为作战配备发数，即杀伤一个目标所需导弹的发数。

由式(4)可知，导弹战备完好性和任务成功性指标量值P1、P2要受到P0、P3、P4、n、W (n)的约束。

为简便起见，如果不考虑对抗敌方袭击概率和突防概率，即令 P0=1、P3=1，对于P4综合考虑落点精度、弹头威力，目标为点目标时，若取保守预测结果为P4≥0.7，则式(5)可改写为：

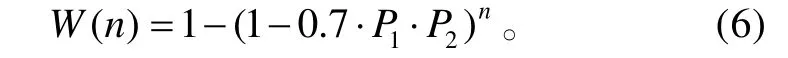
由于新型反舰导弹要求导弹由贮存转入发射阵地时不做技术准备工作，经过转运直接进行舰艇、飞机等作战平台的装载。因此，导弹整个贮存阶段的战备完好性通过发射准备完好率同步反映。

发射准备完好率是指接到作战准备命令后，贮存状态的导弹装备经过转运、平台装载，在发射准备结束时按规定要求完成发射准备的概率。其一般表达式为

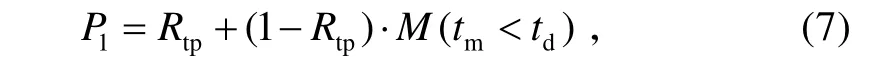
式中：Rtp为在发射阵地所具有的可靠度，由平均贮存可靠度和发射准备时的工作可靠度 Rjz决定，即而其中 tj为进入发射阵地后的发射准备时间，MTBF为平均故障间隔时间；M (tm＜td)为发射准备阶段能修复的概率，其中 tm为在发射阵地的故障恢复时间(包括修复时间和保障延误时间)，td为在发射准备阶段能用来进行维修工作及延误的时间。

因此，式(7)也写为：

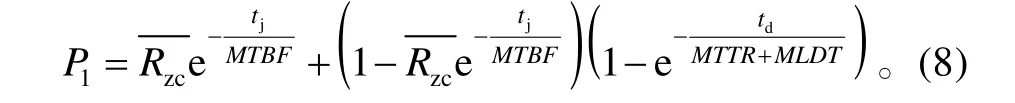
发射准备完成后，接到发射指令到导弹发射一般时间均较短，这时导弹在发射阵地都视为不可修系统。因此，任务成功性P2的分解模型为

式中：Rfs为发射可靠度；Rfx为飞行可靠度。

将式(8)、(9)代入式(6)中可得

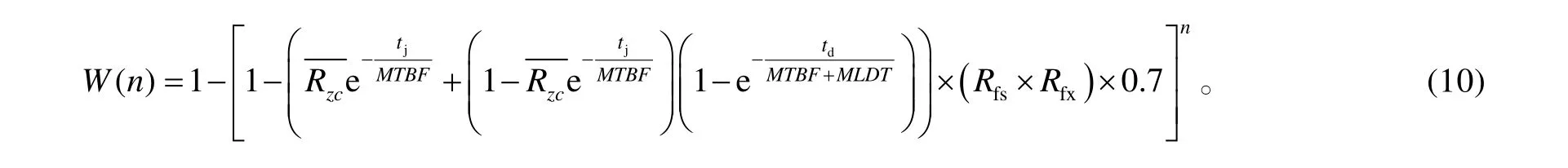
由式(10)可知，该型导弹作战效能主要由平均故障间隔时间MTBF、平均修复时间MTTR、平均保障延误时间MLDT、发射准备时间 tj、允许维修与保障延误时间 td、贮存可靠度、发射可靠度Rfs、飞行可靠度 Rfx等保障性参数决定。

2.2 新型反舰导弹费用模型

根据2.1 效能模型研究结果，需要收集以往相似导弹装备的如下历史数据：MTBF、MTTR、MLDT、发射准备时间、允许维修与保障延误时间、贮存可靠度、发射可靠度、飞行可靠度以及总拥有费用。然后，根据所收集的数据，进行多元回归分析，即可得到各保障性指标与总拥有费用之间的估算关系，从而建立导弹的费用模型。这里，可以采用非线性的多元回归模型，即假设

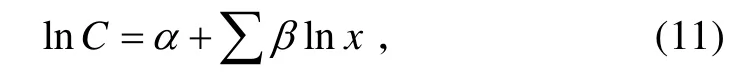
式中：x表示各保障性设计参数的值；α β、为回归模型的待估参数；C为总拥有费用。

假设通过参数估计得到反舰导弹费用模型可表示如下形式：

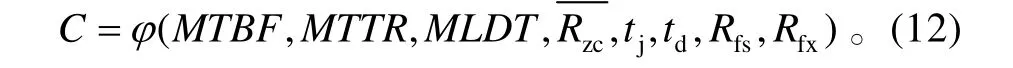
2.3 新型反舰导弹保障性指标权衡模型

导弹保障性指标权衡的目的包括两个方面：一是提高作战效能；二是降低寿命周期费用。因此，本文所建立的权衡模型分为作战效能模型和费用模型两部分，其中作战效能模型作为权衡的约束条件，费用模型作为权衡的目标函数。

设已知各保障性指标的取值范围，且要求反舰导弹的战备完好率要不低于 P1*，任务成功率要不低于 P2*，则根据以往数据和所建立的发射准备完好率模型和费用模型，以“总拥有费用最低”原则建立如下权衡优化模型：

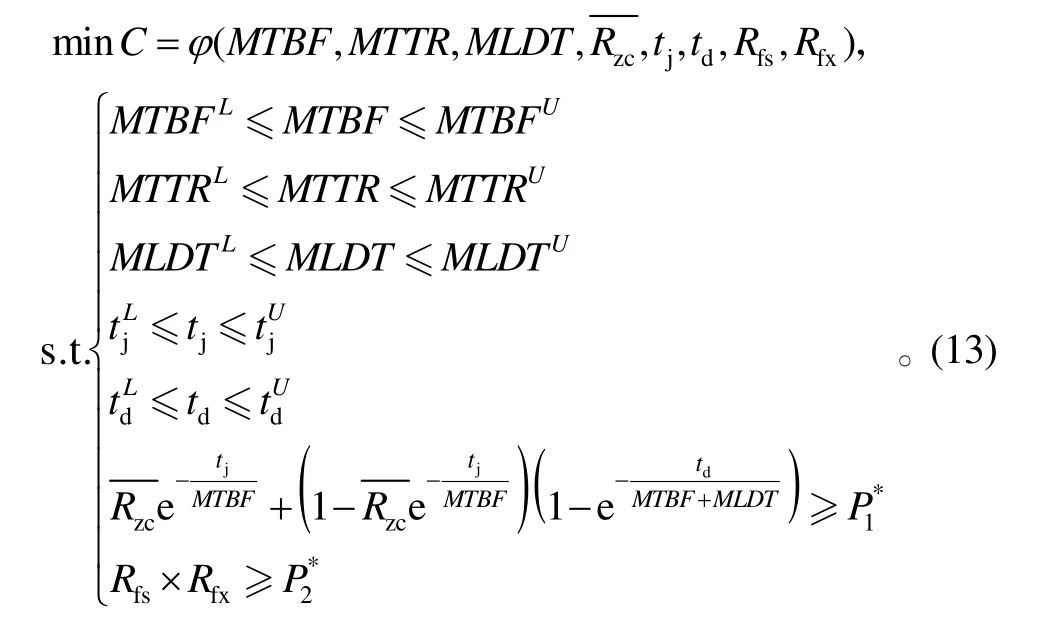
通过求解上述模型，可以得到满足反舰导弹作战需求的最佳保障性设计指标值及对应的作战效能和最低总拥有费用。

由于该优化权衡问题可能存在非凸、不连续和多极值的特点，因此对这类问题的求解往往需要采用智能搜索算法，如遗传算法、蚁群算法、模拟退化络等。

2.4 示例

收集整理以往反舰导弹设计参数和费用统计数据，见表1。

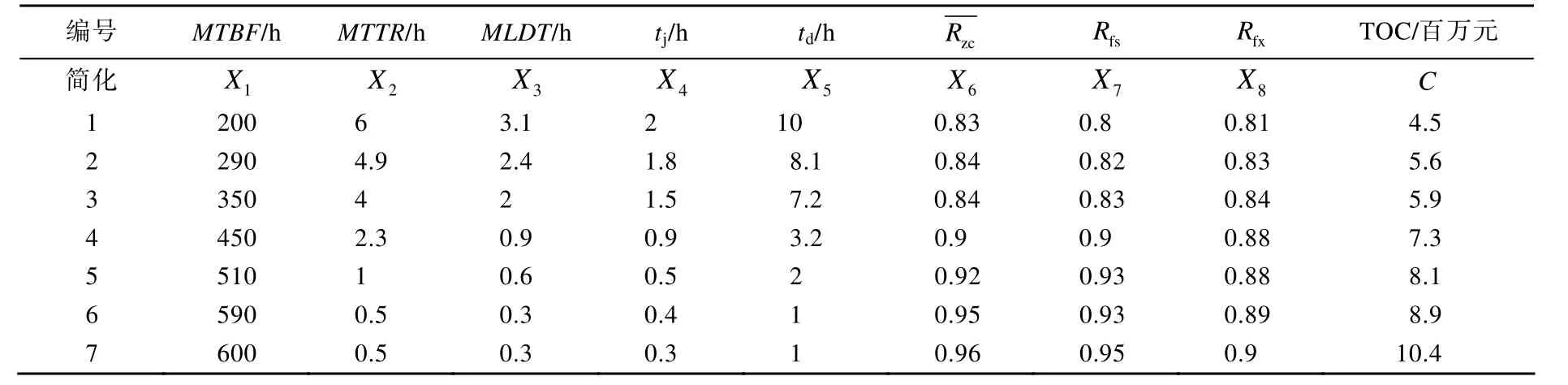
表1 各设计参数与总拥有费用的统计数据

令Y=lnC，xi=lnXi，本例采用岭回归分析得到费用估算模型：

该估算模型仅当各参数在权衡空间内取值时有效。

在本例中，将各参数的取值范围规定如下：

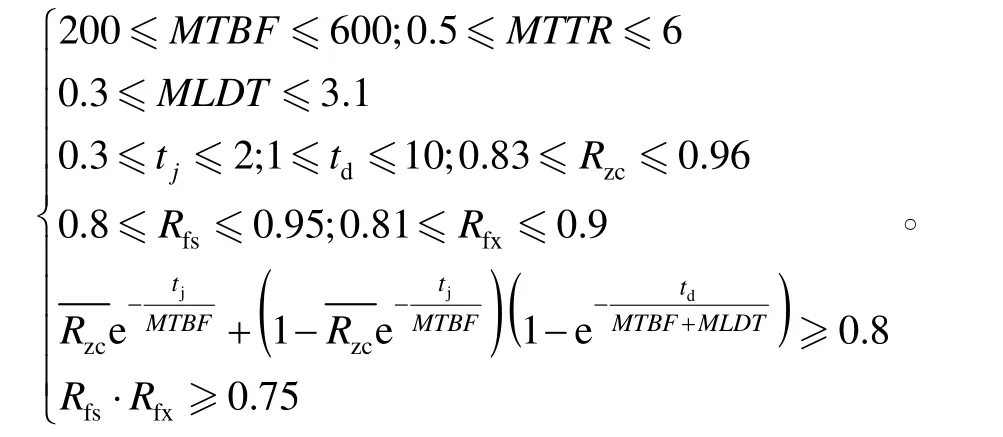
各参数取值范围可由表1获得，后面两条约束条件分别为反舰导弹的发射准备完好率和任务可靠度要求。

将上述费用模型和参数取值范围代入式(13)，并利用遗传算法进行优化计算，采用实数编码，种群规模为20，变异概率取0.2，交叉概率取0.3，在经过500次迭代之后达到稳定。这时得到的最优决策变量为：

其目标值minC=8.3917。

由这个例子可以看出，通过建立CAIV 权衡模型，能够在给定导弹战备完好性和任务成功性要求的情况下，求得成本最低的各保障性参数值。

3 结束语

为了实现某反舰导弹低成本保障的目标，本文利用CAIV方法建立该型导弹关键保障性指标、作战效能和总拥有费用三者之间的关系模型，并采用最优化方法计算得到三者之间的最佳平衡点。

采用该方法进行权衡分析时应当注意：费用模型中参数的估计需要大量以往相似导弹装备历史数据，在今后工作中应注意寿命周期内相关数据的收集和整理，建立完善的保障性分析数据库；本文所建立的作战效能模型是建立在一定的理想条件和假设基础上的，仅对一些关键保障性指标进行了权衡研究，然而影响总拥有费用的因素还有很多，既包括关键的性能参数，也包括非关键参数，因此在形成最终决策前需进行风险分析。

[1]谭云涛,郭波.基于CAIV的武器装备费效分析与指标决策方法研究[J].系统工程理论与实践,2007,27(11):48-53.

[2]张桂永,胡波,汤礼建.电子对抗作战系统装备费效分析[J].舰船电子对抗,2008,31(2):44-45.

[3]李晓斌,解红雨,青龙,等.高压强固体火箭发动机性能/成本优化设计[J].固体火箭技术,2004,27(1):16-19.

[4]吕建伟,陈霖.舰艇设计的费用限额确定方法探讨[J].舰船科学技术,2003,25(5):90-92.

[5]刘晓东,张恒喜.飞机可靠性与研制费用相关关系研究[J].空军工程大学学报:自然科学版,2000,1(1):63-66.

[6]张晓春,刘将军,韩玉启.军用装备可靠性与费用的参数估算方法[J].现代雷达,2003,25(9):51-53.

[7]高尚.可靠性与维修性指标综合权衡[J].系统工程与电子技术,1998,20(10):78-80.

[8]余仁波,徐廷学,李田科,等.基于主客观权重一致的导弹保障性评价[J].四川兵工学报,2011,32(3):9-12.

[9]RONALD LUMAN.Quantitative Decision Support for Upgrading Complex Systems of Systems[D].School of Engineering and Applied Science of the George Washington University,1997:9-19.

[10]MICHAEL BOUDREAU,SENIOR LECTWER.Using Lost as an Independent Variable(CAIV) to Reduce Total Ownership Cost[D].Monterey,California:Naval Postgraduate shod,2006:1-8.

[11]HENRY APGAR.Cost as an Independent Variable(CAIV):A Process and Methodology to Acquire and Operate an Affordable System by Setting Aggressive Life-Cycle-Cost Targets and Trading off Performance,Cost,and Schedule[M].Alexandria VA:American Institute of Aeronautics &Astronautics,2001:1-24.

[12]谭云涛.武器装备费用、性能与RMS 综合优化设计方法研究[D].长沙:国防科学技术大学,2007:17-30.

[13]刘白羽,黄金元,史宪铭.CAIV技术研究现状综述[J].四川兵工学报,2009,30(9):145-148.

[14]孙伟玮,李海军.空舰导弹维修经费投入结构分析[J].四川兵工学报,2010,31(9):120-131.

[15]曹小平,等.保障性论证[M].北京:海潮出版社,2005:122-140.