基于性能参数残差序列分析的发动机性能衰退研究

谭 巍，李本威，李 冬，王永华

（1.海军航空工程学院飞行器工程系，山东 烟台 264001；2.海军飞行学院，辽宁 葫芦岛 125001）

性能衰退是发动机使用不可避免的过程。对发动机进行性能衰退方面的研究是保证发动机安全工作、发现及排除故障、实现发动机视情维修、延长发动机使用寿命的一种重要技术途径[1]。

发动机出现性能衰退后，性能参数开始出现缓慢变化，而性能衰退到达一定程度时，很可能会出现较大程度的下降，预示着故障的发生。因此，性能参数的变化包含着发动机性能衰退的许多信息，是发动机性能衰退程度的重要表征。本文通过分析性能参数残差随时间的变化规律，进行发动机性能衰退程度方面的研究。

1 数据准备

1.1 参数初选

发动机性能衰退的过程中，气路部件气流流通能力和工作效率会逐渐下降，进而造成发动机转子转速及气路中各部件截面的气流温度、压力等征兆参数发生变化。因此，可以通过发动机某一稳定状态各部件截面测量参数的变化情况，随着时间的推移，监测分析发动机性能衰退变化情况。

根据某型发动机所测参数的工程现实，测量参数取为4个，分别为低压转子转速NL、高压转子转速NH、高压压气机压力P3、尾喷口温度8T。4个测量参数组成向量其中，i∈{1,…,p}是发动机序号，j∈{1,…,l}是时间序列序号。性能参数初步选取 8个，分别为低压压气机流量变化量ΔMαf、低压压气机效率变化量Δηαf、高压压气机流量变化量 ΔMαc、高压压气机效率变化量Δηαc、高压涡轮流量变化量ΔMtH、高压涡轮效率变化量ΔηtH、低压涡轮流量变化量ΔMtL、低压涡轮效率变化量ΔηtL。8个性能参数组成向量本文计算数据均采用相对变化量。

全文设计求取性能参数变化量技术路线如图1所示。

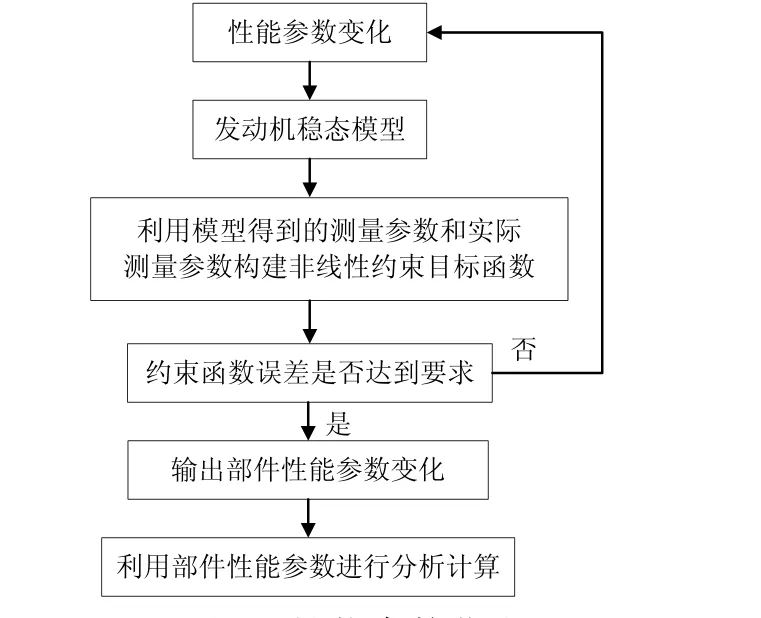
图1 性能参数获取

实际中的测量参数容易受到环境等因素的影响，可能携带大量的误差，因此带入模型计算时首先要经过滤波处理[2]。

如果对8个发动机部件性能参数全部计算，其计算量很大或者根本无解，而根据实际需要，我们也没有必要计算全部8个参数，因为其中某些性能量变化可能对可测参数的影响非常小。因此，进一步分析，从8个部件性能参数中，优化选取起主要作用的性能参数[3]。

1.2 性能参数的优化选取

从定性的方面分析，发动机性能退化主要反映在推力的减少和耗油率的增加上。在尾喷口几何面积不变时，推力的减少主要是通过尾喷管的气流量减少，而燃油流量仅占空气流量很小的比例，因而推力的减少主要是由于空气流量减少引起的，故需要考虑低压压气机流量变化量ΔMaf、低压涡轮流量变化量ΔMtL和高压涡轮流量变化量ΔMtH。耗油率的增加反映转子部件效率的降低，由于涡轮处于高温高压条件下工作，叶片容易变形，使涡轮效率降低。因此，还需要考虑高压涡轮效率变化量 tHηΔ和低压涡轮效率变化量 tLηΔ[4-5]。

通过研究性能参数与输出参数之间的相关性，做出定量分析，找出性能参数对输出量影响程度最大的几个。这里定义相关系数为：

其物理意义是当第m个性能参数变化时，对第n个输出参数的影响程度。进行相关性分析前，先求出相关系数。采用扰动法，分别改变各性能参数1.0%，计算输出量相应变化百分数，当h=0，Ma=0时，扰动性能参数后，输出参数的变化量，见表1。

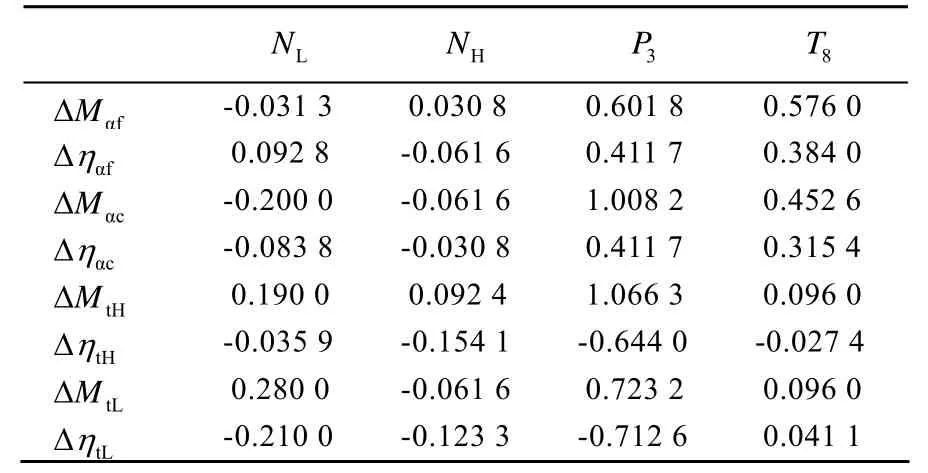
表1 输出参数变化量

从表1中可以看出，发动机测量参数对不同部件性能参数的改变有不同的变化，其敏感程度同样因不同的部件性能参数有显著的不同。为便于分析，找到对某一个输出参数影响最大的性能参数，应对相关系数进行归一化处理，按列归一化原则，按进行归一化，得到归一化参数为：

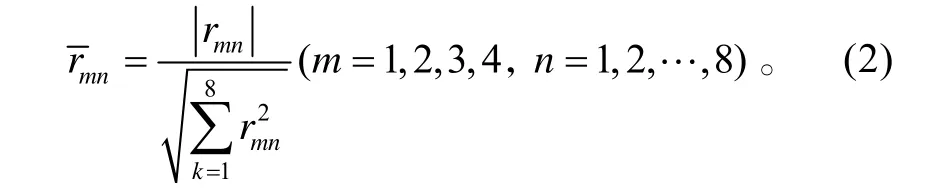
表2是经归一化后的相关系数表，相关系数大于0.5可以认为是强相关，相关系数在0.3～0.5之间为中等相关，相关系数小于0.3为弱相关。对单个部件性能参数变化引起的各测量参数变化率求和，并进行归一化处理，得到如图2所示的测量参数对部件性能参数的敏感图。

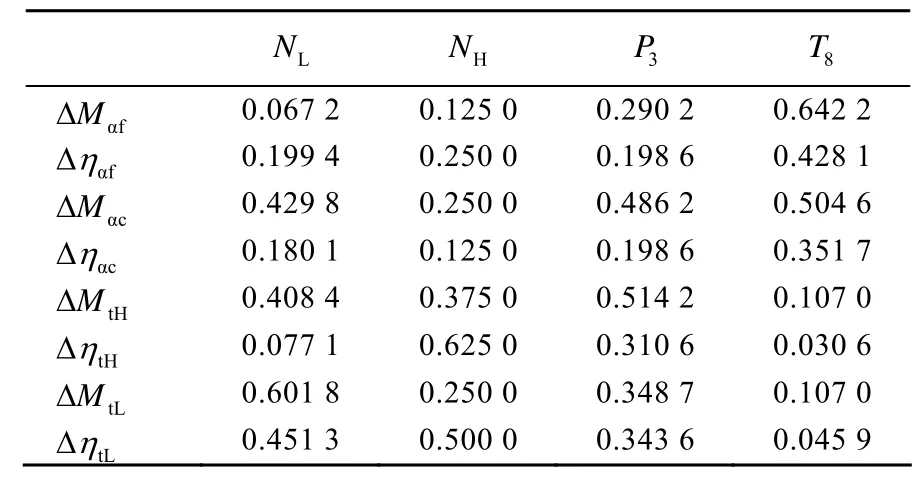
表2 归一化相关系数

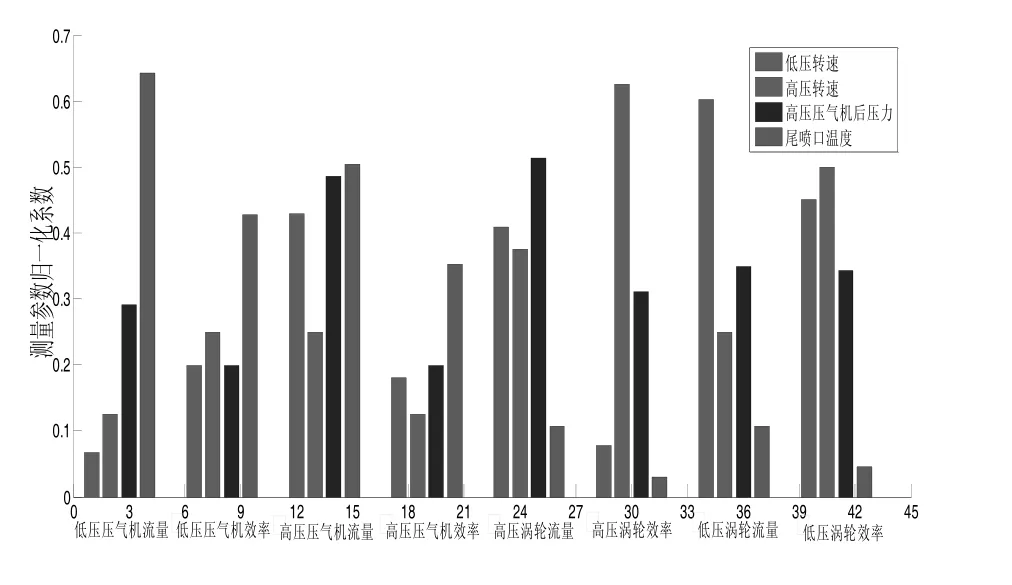
图2 归一化的测量参数对部件性能参数的敏感度

从表2和图2并结合前面的定性分析，本文最终选择的特性参数为：低压压气机流量变化量ΔMaf、低压涡轮流量变化量ΔMtL、高压涡轮流量变化量ΔMtH和高压涡轮效率变化量 ΔηtH。在实际计算中，保留这些参数用于计算，其余舍去，达到了优化参数的目的。此时，选取的测量参数与性能参数个数相等，按照图1的计算流程，则性能参数出现唯一解。

2 性能参数残差时间序列模型的建立

考虑两种类型的性能参数变化现象(性能参数缓慢变化和突变)，文中采用通过残差对比的方法判断性能参数的突变。

采用如下的设计方法，构建性能参数的多元线性回归模型[6-7]，模型如下：

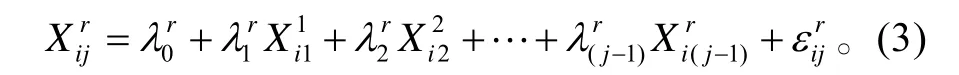
式(3)中：i表示发动机的序号；j表示时间序列序号；X表示发动机性能参数变化；λ表示性能参数的回归因子；ε为拟合后的残差。

利用回归最小二乘法得到发动机性能参数平稳变化部分，与实际值的残差反映性能参数变化趋势，突变后的状况反映性能出现大幅度下降，可能预示着故障的发生，具体算法步骤[8]如下。

1)利用回归最小二乘法拟合性能参数的线性部分[9]。在每一个时间序列点l，对每一台发动机i和每一个标准化的发动机性能参数r，线性模型的参数由下述约束得到：

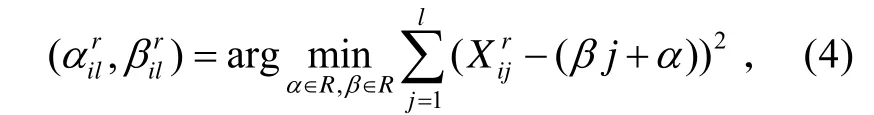
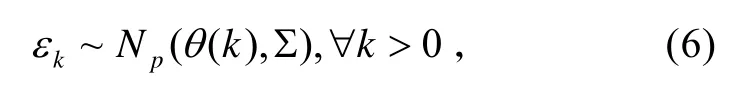
并且

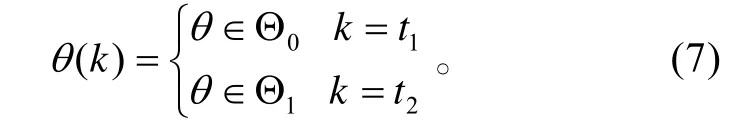
式(7)中：t1、t2是未知时间；Θ0、Θ1是两个空间不重叠的子集；两个超球中心都为θ0。

文中取 θ0=[0,0,0,0][11]，Θ0、Θ1如图3所示。

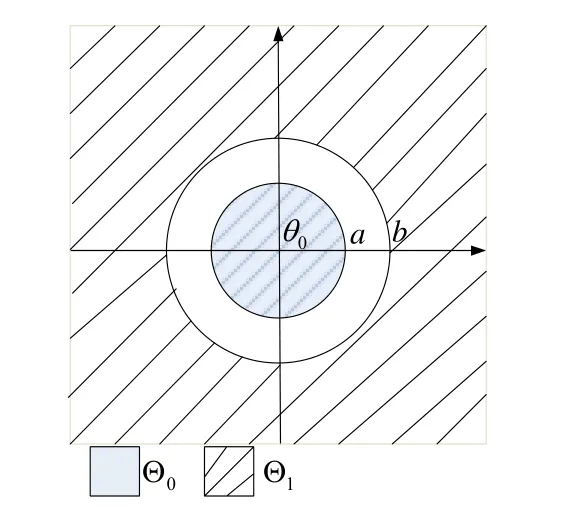
图3 Θ0、Θ1的空间范围

Θ0、Θ1范围定义如下：

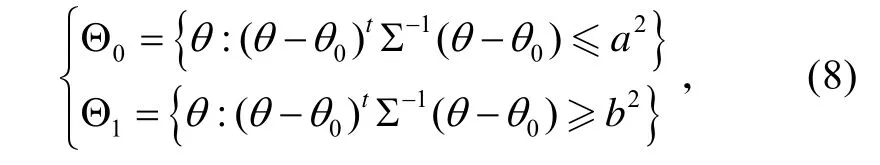
并且，a≤b。

确定性能参数衰退突变点采用的方法：设定时间点αt，表征统计值gk超过特定阈值h的时刻。统计量表示如下：

式(9)中：pθ(⋅)表示均值为θ；方差为Σ 多元高斯分布的密度。此时，Skj表示为：

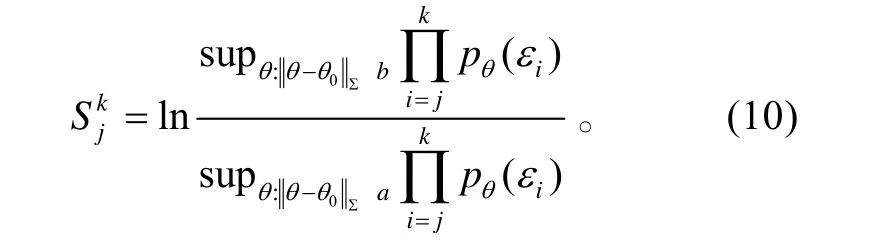
在服从高斯分布情况下，最大值问题式(9)有解析解。此时，Skj表示为：

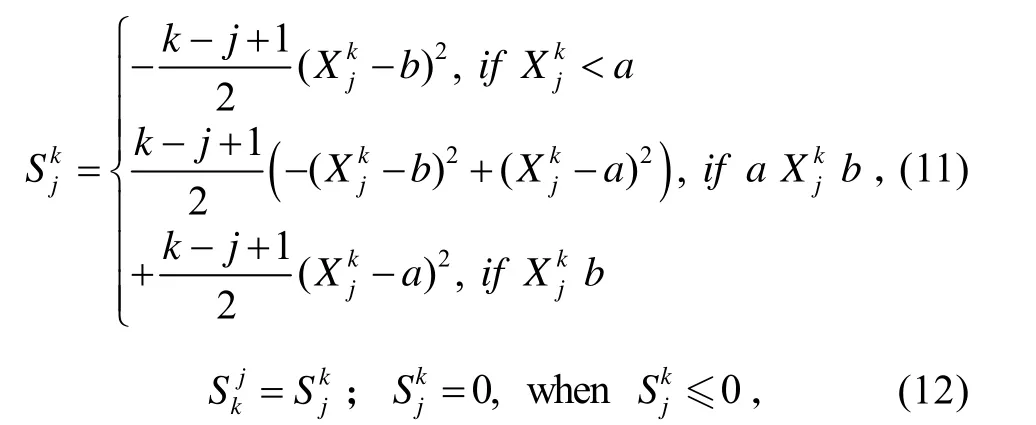
3 仿真分析

选取发动机在最大运用状态下随着日历时间历程的4个测量参数代入发动机模型进行计算，输出部件性能参数变化，最后得到性能参数残差序列，选取其中的某两段进行分析。

3.1 缓慢衰退过程分析

图4是性能参数缓慢衰退的残差示意图，其中横坐标n为性能参数的时间序列点，纵坐标为选取的4个性能参数残差，图5是由上节算法得到的性能参数缓慢变化对应的突变时刻，当Z坐标出现大于0的点时，判断性能出现突变；从图5中可看出，对于性能参数缓慢衰退过程来讲，不存在突变点。

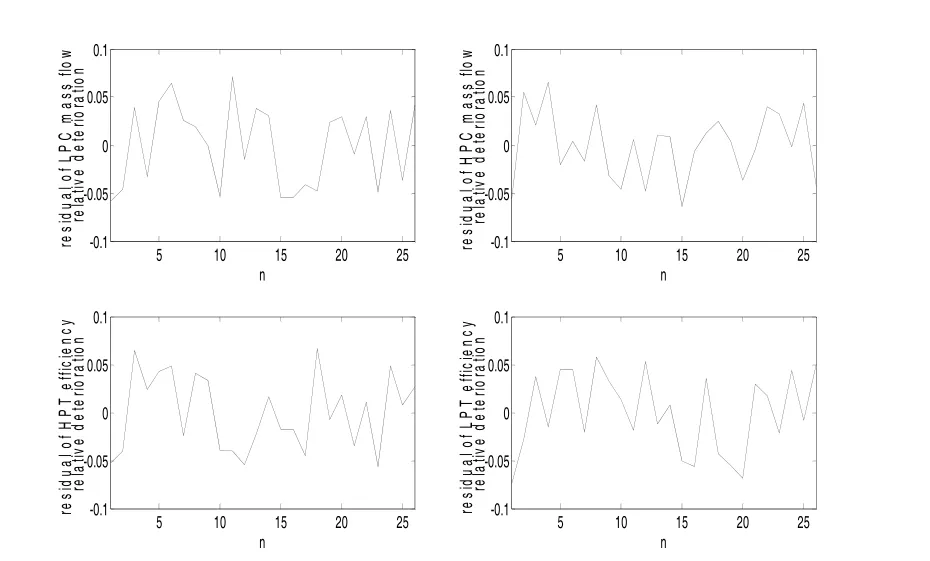
图4 性能参数缓慢衰退残差

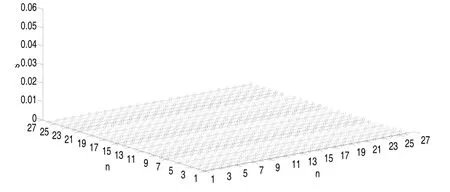
图5 性能参数缓慢衰退对应的突变时刻

3.2 性能突变时刻的确定

如图6、图7所示。

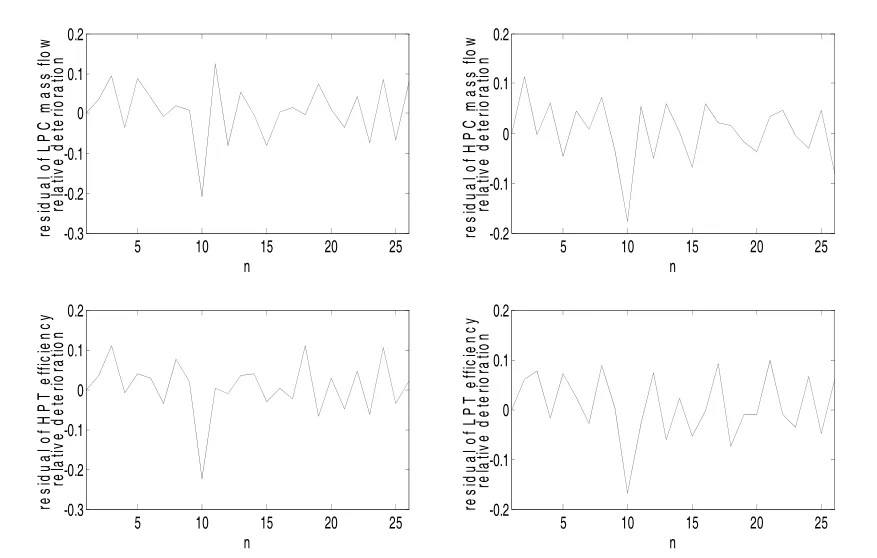
图6 性能参数残差变化的时间序列

图7 性能参数残差变化对应的突变时刻

图6是性能参数残差随时间变化的示意图。可以看出，4个性能参数残差在接近时刻10时，残差开始出现下降，预示性能参数开始出现突变。当到达时刻点10时，4个性能参数残差绝对值达到最大；另一方面，利用上节确定性能突变时间点的算法后，准确的定位了性能参数发生突变的时刻，见图7。

4 结论

本文利用发动机模型进行发动机测量参数对部件性能参数的敏感度分析，优化选取充分表征发动机性能衰退的部件性能参数。通过构造性能参数残差序列，分析性能参数残差随时间的变化规律，对发动机性能衰退进行研究。通过对残差序列的统计量分析，确定性能衰退突变时刻。当性能参数残差达到最大时，发动机性能会发生突变。经过仿真算例分析验证了所建模型和所用算法的有效性，为发动机的维护起到了一定的指导作用。

[1]廉筱纯,吴虎.航空发动机原理[M].西安∶西北工业大学出版社,2001∶101-104.

[2]李本威,尹大伟,王永华,等.某型涡扇发动机状态模型修正[J].海军航空工程学院学报,2008,23(2)∶214-216.

[3]尹大伟.某型发动机模型修正研究[D].烟台∶海军航空工程学院,2007.

[4]程礼,李全通.航空发动机状态监控与故障诊断[M].西安∶空军工程学院,1997∶31-34.

[5]李建国,李本威.航空发动机故障诊断方程的求解及应用[J].燃气涡轮试验与研究,2002,15(2)∶8-11.

[6]马逢时,何良材,于明书,等.应用概率统计[M].高等教育出版社,1989∶230-241.

[7]司守奎.数学建模算法与程序[M].烟台∶海军航空工程学院,2007∶144-157.

[8]徐文彬,齐勇,侯迪,等.基于时间序列分析的应用服务器性能衰退模型[J].西安交通大学学报,2007,41(4)∶427-429.

[9]ETIENNE CÔME,MARIE COTTRELL,MICHEL VERLEYSEN,et al.Aircraft engine health monitoring using self-organizing maps[C]//Proceedings of the Industrial Conference on Data-Mining.Springer,2011∶1-10.

[10]MARIE COTTRELL,PATRICE GAUBERT,CÉDRIC ELOY,et al.Fault prediction in aircraft engines using self-organizing maps[C]//Proceedings of the Industrial Conference on Data-Mining.Springer,2009∶37-44.

[11]BASSEVILLE M,NIKIFOROV I.Detection of Abrupt Changes∶Theory and Application[M].1993∶12-24.