基于TV-L1模型的多尺度遥感影像分解方法

汪秀莉，沈 剑，吴华丽，王 蓉

（海军航空工程学院 a．训练部；b．接改装训练大队；c．控制工程系，山东 烟台 264001）

遥感影像的研究一直备受关注，尤其是遥感影像中的目标提取和识别。近年来针对图像进行分解研究是大势所趋，将一幅遥感影像分解为2 大部分：包含大尺度变化的结构分量以及包含图像小尺度纹理的细节分量[1]。针对不同的目标，提取相应尺度的信息进行处理，这既可以消除其他无用的尺度信息对处理结果的影响，也简化了处理的难度和复杂性，是遥感影像目标识别的有效的预处理方法[2-3]。本文对TV-L2模型和TV-L1模型进行了对比研究，发现两者都具有全变分分解的优点，可以实现遥感影像的分解，但采用TV-L2模型分解有分解不彻底的问题，而TV-L1模型聚集能量、保持边缘的特点能够解决这个问题。本文采用TV-L1模型结合图像多尺度分解方法，提出了一种基于TV-L1模型的多尺度遥感影像分解方法(以下称本文方法)。

1 TV-L2模型

1992年，L.Rudin、S.Osher 和E.Fatemi 提出了利用全变分作为正则化项进行图像分解的模型[4]：

式(1)中，u和f分别是输出图像和输入图像。式(1)由2 部分组成，前半部分是图像的全变分，也就是TV 能量，依赖于图像的变差幅度，是一个正则化项；后半部分是拟合项，或者称为保真项，由它来控制输入图像和输出图像的差异，是输出图像和输入图像的2ℓ 范数，它主要起保留原图像特性和降低图像失真度的作用。λ是Lagrange乘子加权系数，在TV 范数项和拟合项之间起着重要的平衡作用。该模型用图像函数的TV 来作为衡量“最优”的尺度，被称为TV-L2模型[4]或ROF 模型。

2 多尺度遥感影像分解方法

TV-L2模型虽然早已提出并被广泛使用，但该模型只是研究人员根据经验和实验而得，并没有严密的数学理论基础。近年来，随着压缩传感理论的提出[5-8]，TV 模型的理论基础得以证实，同时1ℓ 范数也开始被广泛采用。

2.1 TV-L1 模型

利用图像的梯度结构的稀疏性，可以将压缩传感理论在二维图像中改写为TV-L1的形式，即TV-L1模型[9]：

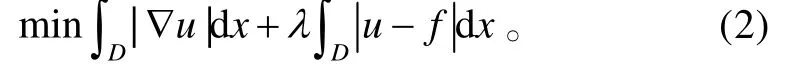
式(2)也是一个凸优化问题。前半部分的 ()TV u可以看作是图像中稀疏信号的1ℓ 范数，后半部分的拟合项，也是1ℓ 范数。于是，式(2)可以通过最小1ℓ 范数法求解。

ℓ1范数具有聚集能量到特征明显处，同时抹平细小特征的特点，TV-L1模型是基于1ℓ 范数的，具有1ℓ 范数的优点，因而TV-L1模型在尺度空间比TV-L2模型有更好的表现。在尺度空间， ℓ1范数平滑的效果是“尽可能”地干净，而 ℓ2范数对小尺度结构的平滑效果不是很干净，在只有一个结构的尺度下仍能看出其他结构的模糊轮廓。

TV-L1模型在不同尺度下得到的结构不同，因而在尺度空间可以很好地将不同的结构区分开来。随着参数λ取值逐渐变小，小的结构依次被平滑掉，而且平滑的效果很干净，这个效果正是多尺度分解的关键。与此同时，保留下来的结构中细节很清楚，这点对于图像分解是很重要的。

2.2 本文方法

基于 ℓ1范数的TV-L1模型在尺度空间分解不同尺度下的结构的效果很好，TV-L1模型在尺度空间随着迭代次数的增加，从小到大依次抹去结构，而保留下来的结构中很好地保持了细节，TV-L1模型可以很好地实现图像多尺度分解。因此，本文提出了一种基于TV-L1模型的多尺度遥感影像分解方法，本方法得到的分解结果具有平滑干净、保持边缘的特点。

基于TV-L1模型的多尺度遥感影像分解方法是将原始图像通过TV-L1模型处理，将得到的图像定义为结构分量，将输入图像与结构分量的差值定义为细节分量，实现图像的分解。结构分量被作为输入图像，再次通过TV-L1模型进行分解，得到下一层次的结构分量和细节分量，并依次迭代，从而实现图像的多尺度分解。

对图像f进行多尺度分解的步骤如下：

1)输入待处理图像f；

2)利用TV-L1模型对图像f进行优化处理；

3)得到结构分量B=f'；

4)利用输入图像与结构分量作差D=f−f'，提取细节分量；

5)判断分解是否结束？是，转7)；否，转6)；

6)将3)中得到的结构分量作为下一次分解的输入图像f，并调整λ参数值，转2)；

7)输出提取的结构分量和细节分量。

按照图像分解模型f=B+D，输入图像f可表示为

式中：D1,D2,… ,Dn依次是由细到粗的细节信息；Bn是大尺度的基本结构。

由上述分解步骤可以给出通过TV-L1模型进行多尺度图像分解流程如图1 所示。

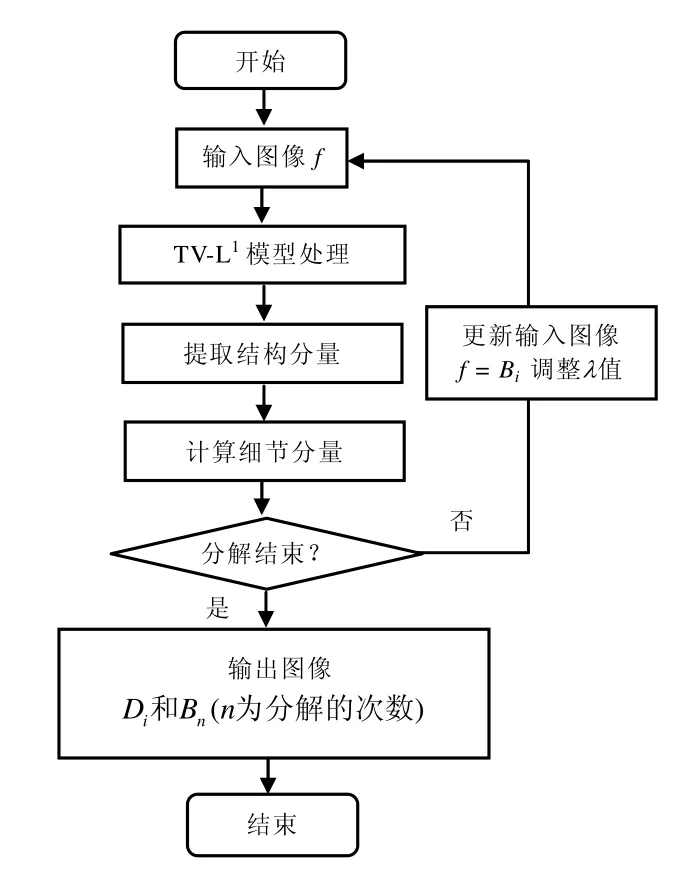
图1 多尺度图像分解流程图

原始图像按照尺度从小到大分解为一系列“由细到粗”的纹理分量和一个大尺度的结构分量。纹理分量描述了图像的细节信息，适用于基于纹理细节的识别方法，也可用于边缘检测、纹理分析等图像分析处理。结构分量体现了图像的基本结构、基本变化趋势，符合基于图像基本特征的分割和目标识别等处理的要求。另外，本文方法通过TV-L1模型中的参数λ来调节尺度，对尺度有定量的描述，通过调节控制尺度，可以分解得到含有噪声的细节分量，实现去噪。

3 实验结果及分析

分别采用TV-L2模型和本文方法对一幅遥感影像做分解实验，图片选自中国科学院对地观测中心(CEODE)的西沙群岛遥感影像。实验所用的计算机的CPU 是Intel Pentium D 2.8 GHz、内存为2 GB，在Matlab 7.11 上实现。

3.1 本文方法实验结果

采用本文方法对西沙群岛遥感图像进行分解的实验结果如图2 所示。3 次分解依次选用了2、1.5和1 三个不同的尺度，经过3 次分解之后得到3 个细节分量D1、D2和D3以及1 个最终的结构分量B3。式(4)给出了各个分量之间的关系。

图2 多次多尺度分解实例

由图2 可以看出，采用本文方法对遥感影像进行分解可以获得不同尺度下的结构分量和细节分量，并且随着λ的减小，尺度越来越大，结构分量就越来越模糊，而细节分量包含的信息越来越多。

3.2 本文方法特点

分别采用TV-L2模型和本文方法对该遥感影像做分解实验，可以看出本文方法的效果优于TV-L2模型。尤其是本文方法具有的保边、去噪和分解彻底的特点，图3~5 分别说明了这3 个特点。

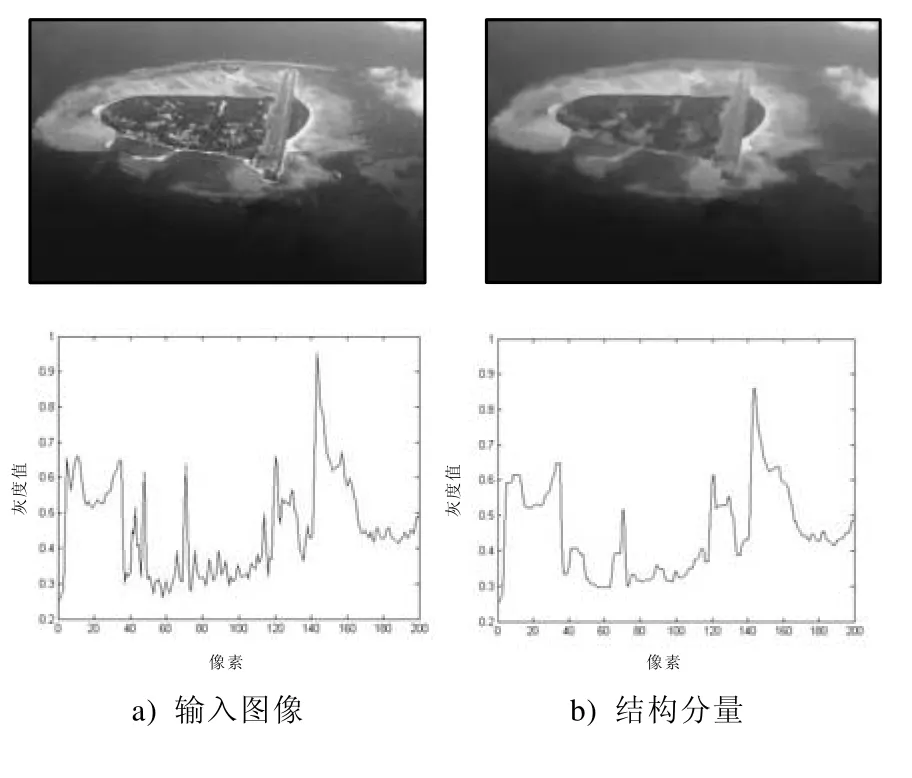
图3 保持几何形状示意图

图3 a)是输入图像，图3 b)是采用本文方法分解得到的结构分量，提取黑线位置所在行的一维信号，可以看到图像的边界和高对比度细节。对比输入图像和结构分量的一维信号，可知本文方法在分解时保持了几何形状，具有保边的特点。

图4 是对一幅噪声图像分别采用本文方法和TV-L2模型进行图像分解的结果，得到的结构分量和细节分量分别见第1 列和第2 列。采用本文方法得到的细节分量中只有噪声，没有图像的其他信息，而采用TV-L2模型分解得到的结构分量中，图像本身已模糊，即图像本身的信息已经被分解，但是结构分量中依旧含有噪声，因而不能分解噪声。通过对比可以明显看出采用本文方法分解的效果比采用TV-L2模型的效果要好，采用本文方法可以很好地分解出噪声。

图4 去噪效果图

本文方法具有分解彻底的特点，即分解尽可能“干净”。图5 是分别采用TV-L1模型和TV-L2模型进行2 次连续分解得到的细节分量的示意图，即将第1 次分解得到的结构分量作为下一次的输入再次进行分解，2 次分解采用的尺度参数为同一尺度值。

图5 与TV-L2 模型效果对比图

可以看出采用TV-L1模型进行分解时，对于同一尺度的分解，TV-L1模型可以分解得很“干净”，而采用TV-L2模型分解出来的效果则不同于TV-L1模型的效果，采用同一尺度值，对第一次分解得到的结构分量进行第2 次分解时，仍然可以得到包含图像信息的细节分量和继续被分解了的结构分量。对比图5 b)和图5 d)，可以清楚地显示出TV-L1模型分解彻底的特点。

图6 给出了采用本文方法对多幅遥感影像的分解实验结果，第1 列为原始图像，第2 列为分解得到的结构分量。结构分量去除了原始图像中的细节，更好地显现了图像的结构信息，为进一步的图像处理做好了预处理。

图6 多幅遥感影像分解结果图

4 结论

本文根据1ℓ 范数的聚集能量到特征明显处，同时抹平细小特征的特点，选用了TV-L1模型。结合多尺度分解的思想，提出了基于TV-L1模型的多尺度遥感影像分解方法。该方法具有多尺度、去噪、保持边缘和分解彻底的特点。本文通过实验证实了方法的有效性并对比TV-L2模型说明了其特点。该方法可以被进一步的扩展应用，比如遥感影像的增强处理、分割和识别等。本文为遥感影像的后续处理提供了很好的基础和预处理。

[1] KARTIC S, CYRIL S, FRÉDO D. Edge-preserving multiscale image decomposition based on local extrema[J]. ACM Transactions on Graphics, 2009,28(5): 8452-8493.

[2] LI Z, JING Z, SUN S, et al. Remote sensing image fusion based on steer able pyramid frame transform[J]. Acta Optica Sinica, 2005,25(5):598-602.

[3] JIN H Y, LIU F, JIAO L C. A method of image fusion based on multiscale contrast pyramid and directional filter banks[J]. Acta Electronica Sinica, 2007,35(7): 1295-1300.

[4] RUDIN L, OSHER S, FATEMI E. Nonlinear total variation based noise removel algorithms[J]. Physica D, 1992,69(1):259-268.

[5] DONOHO D L. Compressed sensing[J]. IEEE transactions on information theory, 2006,52(4):1289- 1306.

[6] CANDÈS E. Compressive sampling[C]//Proceedings of International Congress of Mathematicians. Madrid: European Mathematical Society Publishing House, 2006:1433-1452.

[7] BARANIUK R G. Compressive sensing[J]. IEEE signal processing magazine, 2007,24(4):118-121.

[8] IVANA S, CLEM W, MUJDAT C. Compressed sensing of mono-static and multi-static SAR[J]. Proceedings of the SPIE, 2009,7337:5.

[9] CHAN ESEDOGLU. Aspects of total variation regularized L1function approximation[J]. SIAM journal on applied mathematics, 2005,65(5):1817-1837.