导弹发射装置随动系统模糊神经PID控制器

赵修平，苏正波，郭 凯，王天辉

（1．海军航空工程学院 a．飞行器工程系；b．研究生管理大队，山东 烟台 264001； 2．海军装备部军械保障部，北京 100841）

某型导弹发射装置的随动系统是采用永磁同步电机的一个非线性多变量系统，传统的PID 控制器难以实现理想的控制效果。随着控制理论的发展，PID 控制与一些先进的智能控制结合被用于复杂对象的控制中，已成为一个发展方向。如模糊PID 控制就是将模糊控制与PID 控制结合，利用模糊控制的推理能力来自动调整PID 控制参数的。[1-3]但模糊控制的控制规则及隶属度函数，一旦建立就无法更新，存在控制精度不高等问题。基于神经网络的PID控制是将神经网络与PID 控制结合，利用神经网络的自学习能力来调节PID 参数[4-6]，但神经网络的结构和权值没有明确的物理意义，这给神经网络的设计及初始化带来很大困难[7]。模糊神经PID 控制是将模糊控制、神经网络及PID 控制结合起来，利用模糊控制和神经网络的互补性，设计一种模糊神经控制器，自动调节PID 控制器的参数索算法[8-9]，把一阶回溯和最好优先结合起来，以便缩小搜索空间，提高得到满意解的速度。

1 发射装置随动系统的数学模型

某型导弹发射装置随动系统是由永磁同步电动机、位置和速度等传感器、晶体管脉宽调制(PWM)逆变器及控制电路等环节组成。图1 是具有位置反馈、速度反馈和电流反馈三闭环结构的方位随动系统原理图。由文献[8]可知，其模型近似地看作是一个二阶对象：

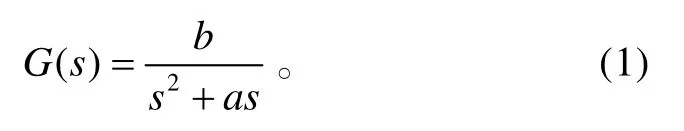
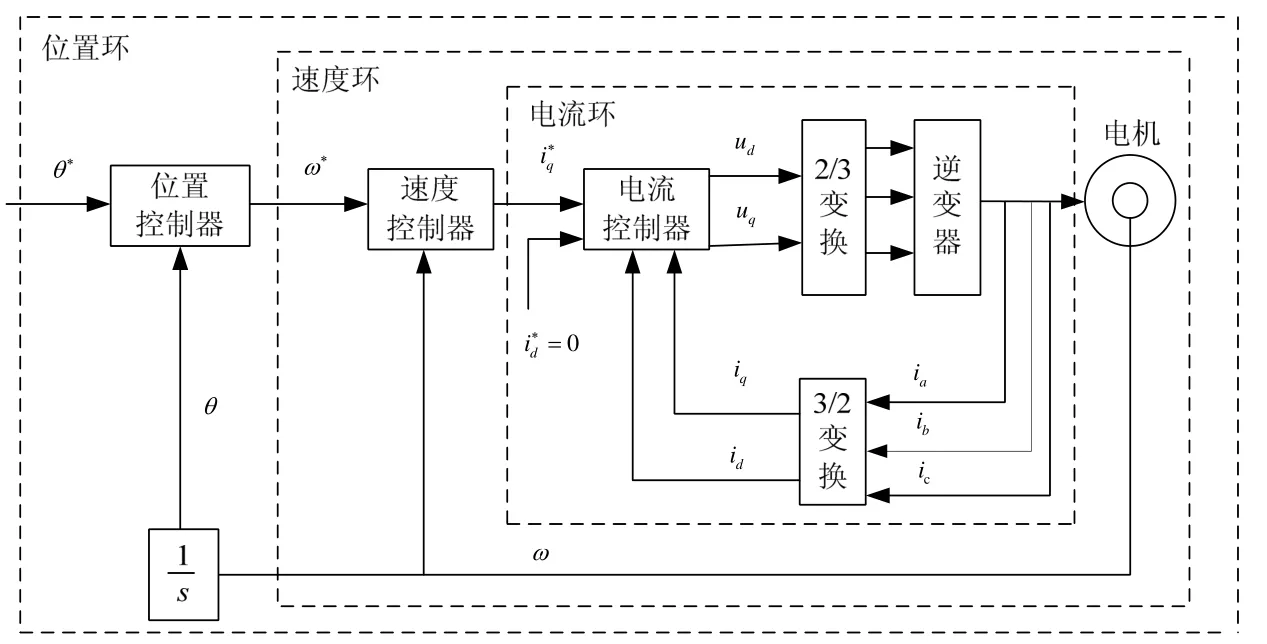
图1 随动系统原理图

2 模糊神经PID 控制器的设计

2.1 模糊神经PID 控制器的结构原理

利用模糊系统和神经系统的等价结构，把模糊控制和神经网络相结合，构成模糊神经控制器。用模糊神经控制器来对传统PID 控制器的参数进行调节，从而构成模糊神经PID 控制器。其原理图如图2 所示。

图2 基于模糊神经网络的智能PID 控制器的原理图

模糊神经网络结构中输出层的神经元个数应设置为3 个，3 个输出分别为PID 控制器的参数kp、ki、kd。该随动系统采用如式(2)所示的增量式PID控制算法，

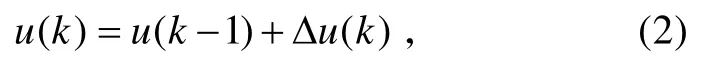
Δu可表示为

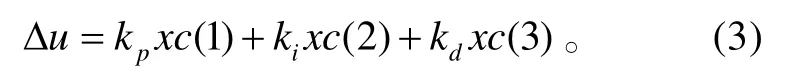
式(3)中：xc( 1) =e(k)；xc( 2) =e(k) −e(k− 1)；

xc( 3)=e(k)−2e(k− 1)+e(k+ 2)。

2.2 模糊神经控制器的结构

模糊神经控制器是用神经网络对模糊控制器的隶属度函数及模糊控制规则进行调整，把误差e和误差变化率ec作为系统的输入量，输入和输出变量均划分为7 个模糊子集，它们的隶属度函数都用高斯函数表示。模糊神经控制器的网络结构见图3。

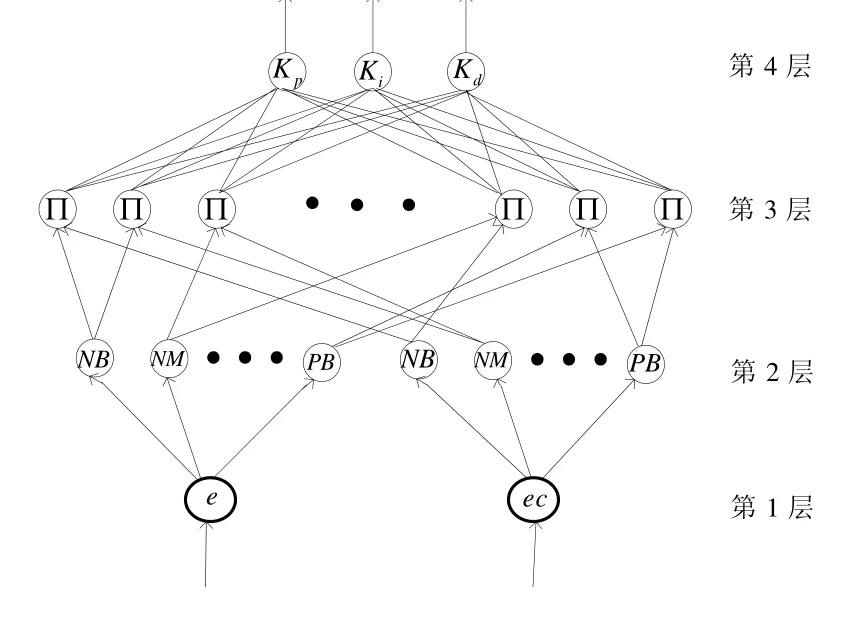
图3 模糊神经控制器结构图

该模糊神经控制器有4 层网络构成，分别为：输入层、模糊化层、模糊推理层和输出层。各层的信号传播及功能如下[9]：

第1 层：输入层。该层的各个节点直接和输入量各点连接，将输入量直接传到下一层。节点数为2，对该层每个节点i的输入输出可表示为

第2 层：模糊化层。该层实现输入变量的模糊化，完成一个隶属度函数的计算，计算出变量相对于每个模糊子空间的隶属度。该层中的每一个节点可代表着与输入变量相应的模糊语言值，节点数为14。在这一层，采用高斯型函数作为隶属度函数，cij和bij分别是第i个输入变量第j个模糊集合的隶属度函数的均值和标准差。

本层的隶属度函为

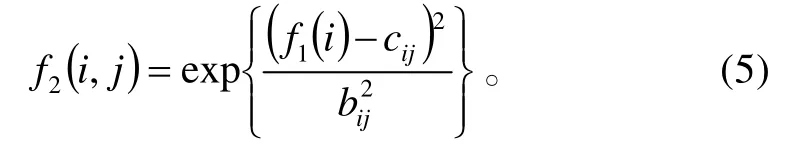
式(5)中：i=1,2；j=1,2, … ,7；f(i)表示输入变量。

第3 层：模糊推理层。模糊推理层是网络中的重要部分，它联系着模糊推理的前提和结论，实现网络的模糊映射。模糊推理层是通过与上一层的连接来实现模糊规则的匹配，该层的各个节点之间可实现模糊运算，即利用各个模糊节点的组合可求出相应的点火强度，然后进行归一化处理。该层节点为49，通过式(6)得到每个节点的输出。

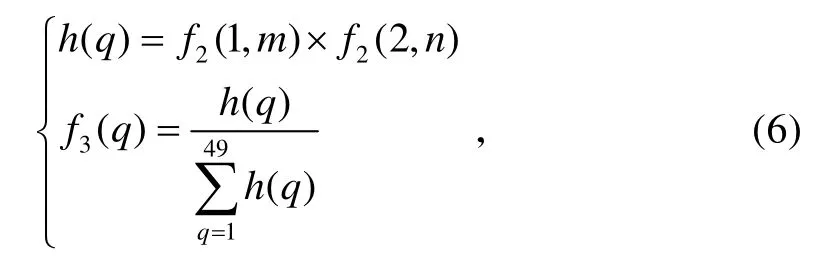
式中：m=1,2, … ,7；n=1,2, … ,7；f(1,m) 和f(2,n)表示输入变量，即第2 层输出量。

第4 层：输出层。该层主要计算模糊神经网络的输出值，经过解模糊化将最终结果输出。该层有3 个神经元节点，节点的输出分别为kp、ki、kd的整定结果。这里有一个第3 层跟本层的连接权值矩阵wpq，它是一个49 行3 列的矩阵。

本层的输出值就是将权值矩阵和第3 层的输出相乘。即，

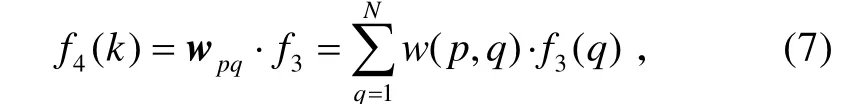
式中：p=1,2,3，q=1,2,… , 49，N=49。

2.3 模糊神经控制器的参数学习

对于所设计模糊神经控制器的参数学习过程就是对权值矩阵wpq和高斯函数宽度cij和中心值bij的参数调节过程。对权值矩阵wpq的调节实现对模糊规则的调节，对高斯函数参数cij和bij的调节实现隶属度函数形状和位置的调节。

通过对参数的调节使目标函数达到最小，这里取目标函数为

式(8)中：θ*为随动系统的期望位置输出，即伺服系统的输入；

θ为随动系统的实际位置输出。

为了使系统的实际输出θ最逼近于系统的期望输出θ*，必须让目标函数E的值达到最小，这里选取Delta 学习规则来计算Δwpq、Δbij和Δcij。

Δwpq可表示为：

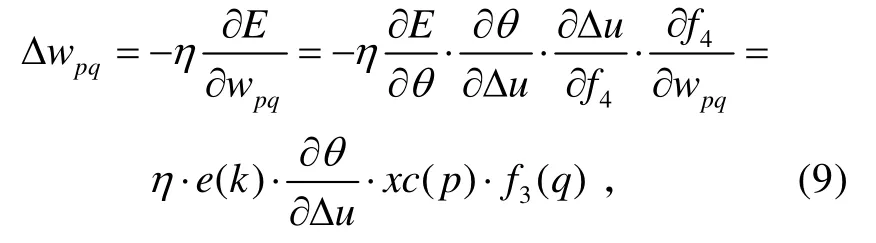
式中，η为学习速率。

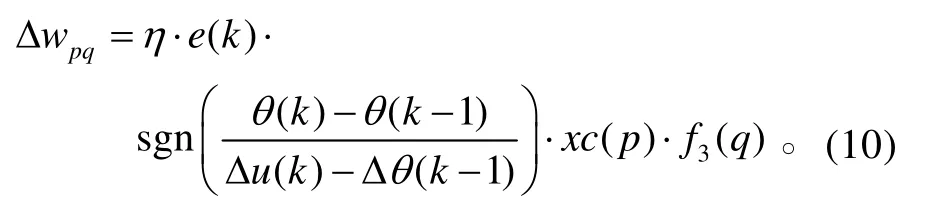
同理可得：

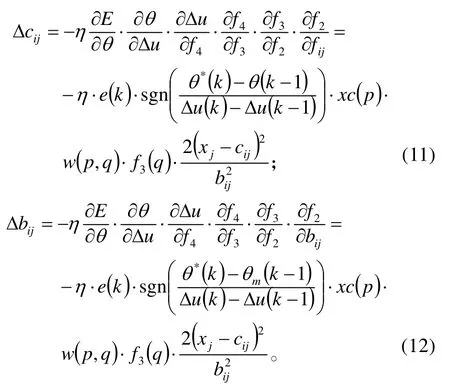
采用一阶梯形寻优算法可以求得：

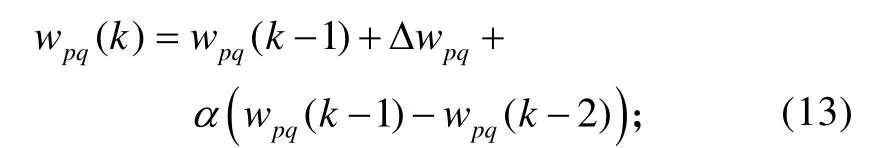
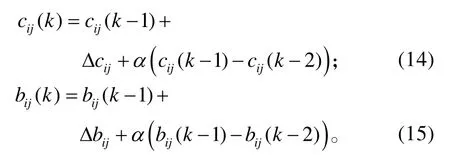
式(13)~(15)中：k为控制器的迭代步骤；α为学习动量因子。

3 系统仿真

3.1 建立仿真模型

在该随动系统中，位置环的作用就是保证系统静态精度和动态跟踪的性能，这直接关系到发射装置随动系统的稳定与高速运行，对整个系统的动静态性能具有重要影响[11]。电流环、速度环为随动系统的内环，传统的PI 控制器可以满足该随动系统对于电流和速度的响应需求[12]。因此，本文主要是对该随动系统的位置环的控制进行研究，对电流环和速度环采用 PI 控制，对永磁同步电机控制采用id= 0的矢量控制。

本文采用matlab/simulink 对该随动系统进行仿真研究，整体的仿真框图如图4 所示。

模糊神经PID 控制器利用s 函数编写，集成为一个模块。为了与模糊自适应控制效果进行对比设计传统PID 控制器。经过不断的测试，在传统的PID控制器中取参数kp= 24、ki= 6、kd= 4时，系统可以达到较好的效果。在对比闭环系统进行仿真前，需要对simulink 仿真环境进行设置，选取算法为ode23t，可变步长，相对误差为0.001 s，仿真时间为10 s，启动仿真结束后，得到仿真曲线。

3.2 仿真结果分析

在t= 0时系统有幅值为100 的阶跃输入，采用模糊神经PID 控制器该伺服系统的位置响应曲线如图5 所示；采用传统PID 控制器该伺服系统的位置响应曲线如图6 所示。从图5 和图6 的对比可以看出在模糊神经PID 控制器下，系统的快速性明显优于传统的PID 控制器，且系统没有超调。

在t= 7时，给系统以一定的负载，其响应曲线如图7 及图8 所示。从图7 和图8 的对比可以看出，在模糊神经PID 控制器的作用下，其随动系统的鲁棒性要优于传统的PID 控制器。

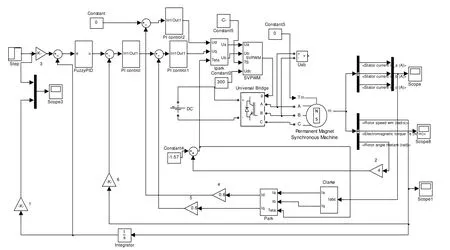
图4 随动系统的整体仿真模型

图5 基于模糊神经网络PID 控制器位置阶跃响应曲线

图6 传统PID 控制器阶跃响应曲线

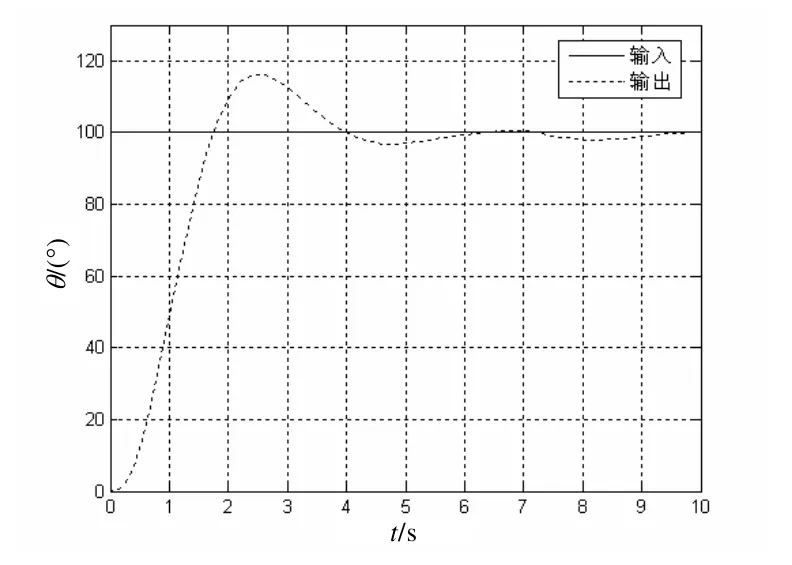
图7 传统PID 控制器下负载干扰阶跃响应曲线

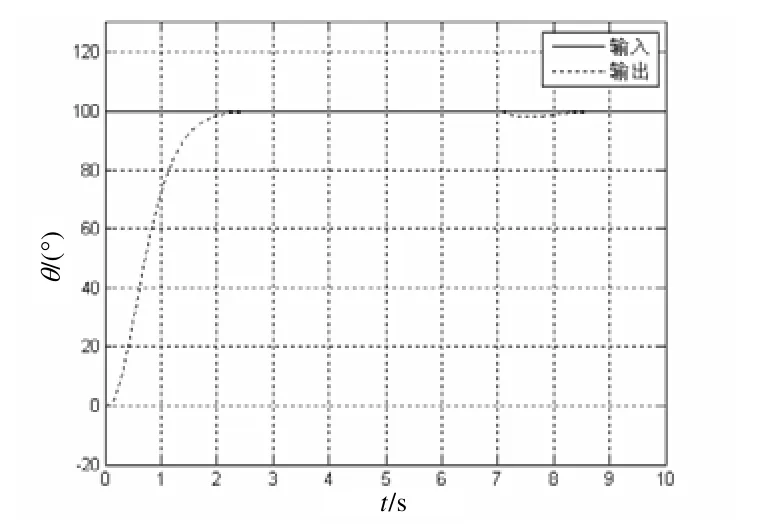
图8 基于模糊神经网络的智能PID 控制器 负载干扰阶跃响应曲线

4 结论

本文将模糊控制、神经网络及传统的PID 控制相结合，根据某型导弹发射装置的随动系统模型，设计了模糊神经PID 控制器。通过和传统PID 控制器的仿真对比看出，在该随动系统中用模糊神经PID 控制器，其动态性能和鲁棒稳定性有显著改善。

[1] 姬伟, 李奇. 自适应模糊PID 控制器在跟踪瞄准线稳定系统中的应用[J]. 控制理论与应用, 2008,25(2): 278-282.

[2] 李晓强, 王丹, 黄加亮, 等. 一种非线性时滞系统的鲁棒性模糊自适应控制[J]. 控制与决策, 2010,25(7): 1045-1049.

[3] SHAYANFAR H A, JALILI A. Multi-stage fuzzy PID power system automatic generation controller in deregulated environments[J]. Energy Conversion and Management, 2006,47:2829-2845.

[4] 姜峰, 段锁林. 基于CMAC 的PD 控制在电液伺服系统中的应用[J]. 计算机仿真, 2011,28(4):152-155.

[5] 王军, 张幽彤, 王宪成, 等. 神经网络结构PID 方法在电液供油提前器中的应用研究[J]. 兵工学报, 2008,29(10):1163-1166.

[6] YE JUN. Adaptive control of nonlinear PID-base analog neural networks for a nonholonomic mobile robot[J]. Neurocomputing, 2008,71:1561-1565.

[7] 程启明, 程尹曼, 郑勇, 等. 基于模糊径向基函数神经网络的PID 算法球磨机控制系统研究[J]. 中国电机工程学报, 2009,29(35):22-28.

[8] 王天辉, 赵修平, 徐广. 某型导弹发射装置伺服系统的滑模控制器设计与仿真[J]. 舰船电子工程, 2011, 31(6):189-191.

[9] LIN F J, WAI R J, LEE C C. Fuzzy neural network position controller for ultrasonic motor drive using push-pull DC-DC converter[J]. IEEE Proceedings Control Theory Application, 1999,146(1):99-107.

[10] 王瑞明. 交流伺服驱动系统新型控制策略研究[D]. 杭州: 浙江大学, 2005.

[11] 尹霞, 黎亚元, 万志伟．数控伺服系统模糊PID 控制仿真研究[J]. 装备制造技术, 2008(10):103-104.

[12] 陈时伯. 电力拖动自动控制系统[M]. 北京: 机械工业出版社, 2010:21-35.