三体船操纵性水动力的势流理论计算

詹金林，卢晓平，李光磊

(1.海军工程大学 船舶与海洋工程系，湖北 武汉 430033;2.海军驻九江地区军事代表室，江西 九江 332007)

三体船由主船体和2个侧体组成，3个船体均较为细长.由于其稳定性、快速性等优良性能，近年来受到广泛关注，在军用和民用上具有十分广阔的前景［1-3］.国内外对三体船的研究也已广泛展开，但在三体船的操纵性方面研究甚少，国外主要有KUN-Jin Kang等开展的研究［4-6］，国内卢晓平、姚迪等对三体船操纵性能进行了计算，定性分析了三体船的操纵特性［7-8］.

本文采用有升力势流理论面元法［9］求解三体船斜流下的流体动力，即横向力、转首力矩以及相应的水动力导数(操纵性位置导数).首先，计算了二维NACA0012机翼在有攻角来流的流场中表面压力系数的分布，并计算了Wigley单体船斜航下的横向力和转首力矩系数，通过与实验数据对比验证了方法的正确性和可靠性.在此基础上，计算了系列片体位置布局下Wigley三体船斜航下受到的横向力和转首力矩以及相应操纵性位置导数.根据计算结果，分析了侧体位置对操纵运动水动力、操纵运动特性以及流场的影响.

1 数学模型

1.1 坐标系

采用如图1所示的右手坐标系.O为坐标原点，位于主船体的中心位置;X轴沿主船中纵剖面指向船尾;Y轴指向主船体右侧;而Z轴垂直于自由面指向上方;侧体对称地分布在主体的两侧其朝向与主船体一致;a为侧体中心位置相对主体中心位置的纵向距离;p为侧体中心位置相对于主体中心位置的横向距离;来流方向为从船头指向船尾，即沿X轴正向.

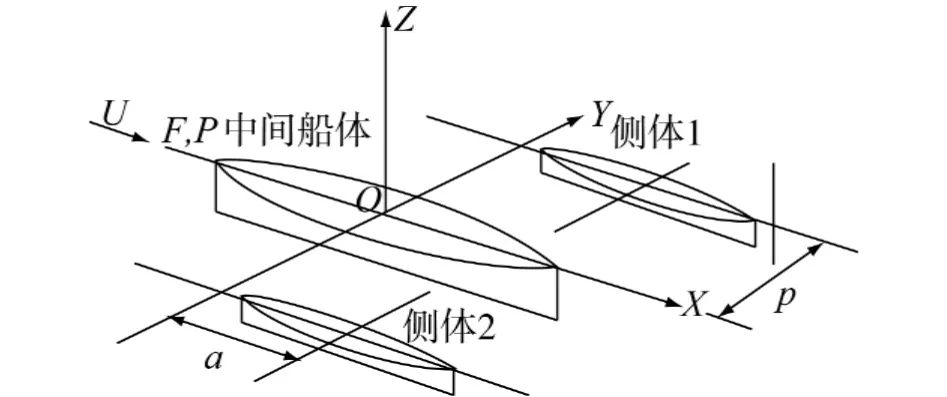
图1 三体船坐标系Fig.1 Reference frame for the trimaran

1.2 控制方程和边界条件

假定均匀来流速度为V0，而其方向与中体中纵剖面的夹角为β，则

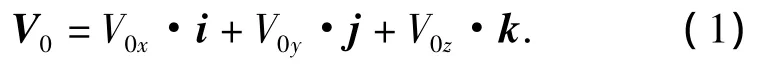
式中:V0x、V0y、V0z分别为来流速度在各坐标轴上的分量.根据势流理论，流场存在速度势Φ，由均匀来流的速度势和扰动速度势φ构成，即

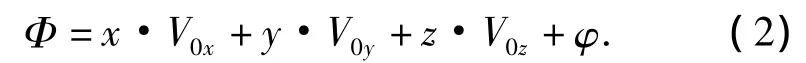
暂不计自由面兴波影响，φ应该满足以下定解条件:

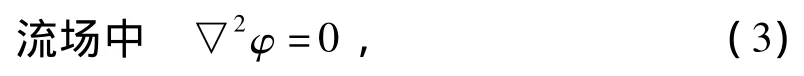
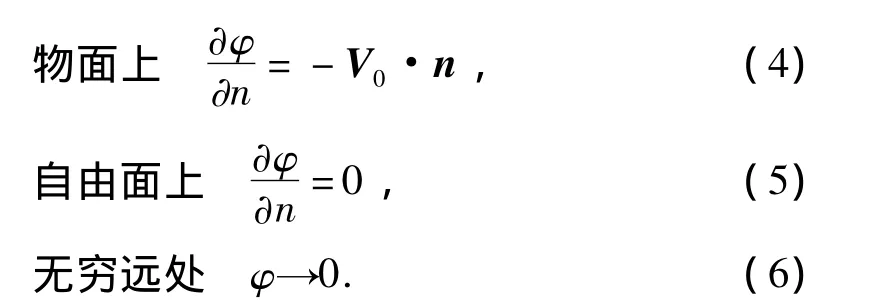
1.3 方程的离散和求解

按由格林定理导出的有升力势流问题速度型面元法，扰动速度势是由分布在物面上和尾涡面上的奇点引起的，物面奇点须取偶极子或涡，根据偶极子分布和涡分布的等价性［10］，物面和尾涡面上的法向速度可表示为

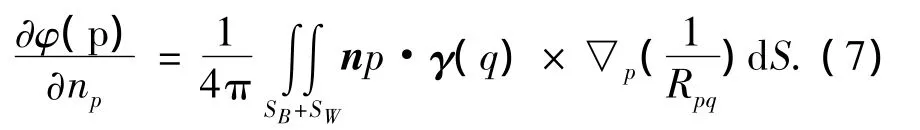
式中:γ(q)=▽Qμ×nQ，p、q分别表示控制点和场点，μ表示偶极子分布强度，SW、SB分别表示尾涡面和物面.将物面和尾涡面划分为若干面元，则面元上控制点的诱导速度为

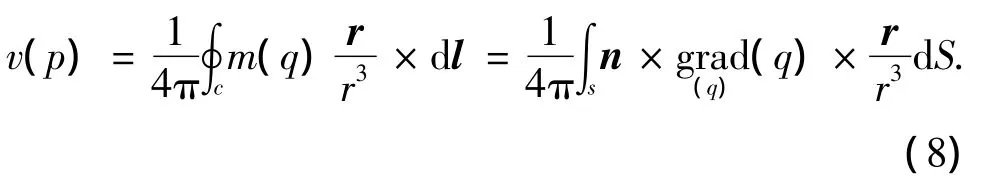
如果面元划分足够小，可以认为每个面元上的偶极子密度是均匀分布的，则式(8)只用考虑前一部分对速度场的影响，即涡环的诱导速度，则点p的扰动速度可以写为:

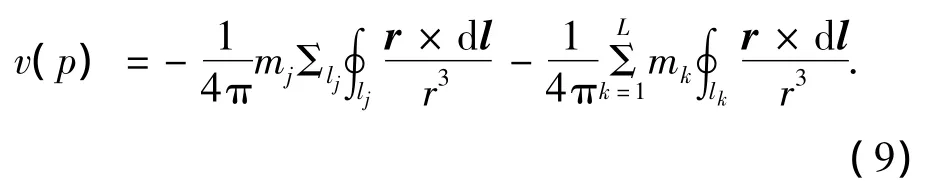
式中:mk为马蹄涡的强度，而m1、m2分别为尾缘上下表面面元的涡强.将物面划分为N个单元，则拥有N个控制点，结合物面条件式(4)，扰动速度表达式(9)，以及库塔条件式(10)，物面边界条件可离散为如下线性方程组:

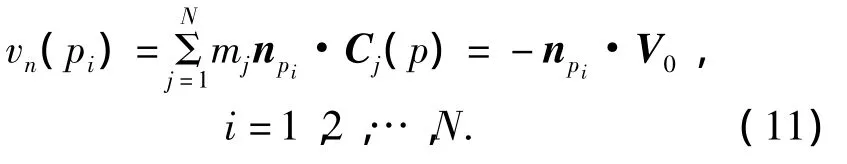
其中，不与物体后缘相邻的单元影响系数为

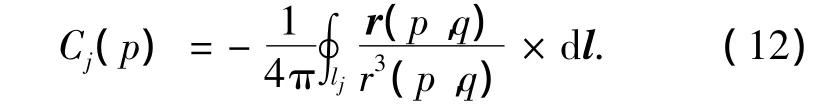
与物体后缘相邻的单元，将尾迹中马蹄涡的影响计入其中，则有

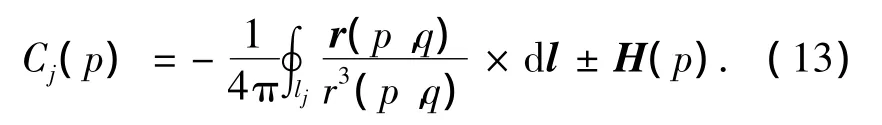
式中:H是单位强度马蹄涡诱导的速度，正号用于上表面单元，负号用于下表面单元.

根据式(11)解出涡元强度后，即可以计算每个面元上控制点的流场速度，并根据伯努利方程得到每个控制点处的压强Pi，再根据:

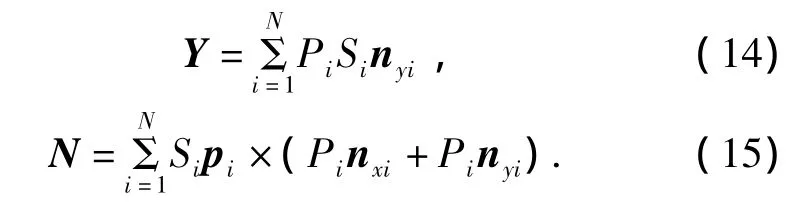
就可以计算船体受到的横向力和转首力矩.

2 计算实例

2.1 算例1

采用NACA0012标准机翼作为算例1，该机翼的剖面图如图2所示.

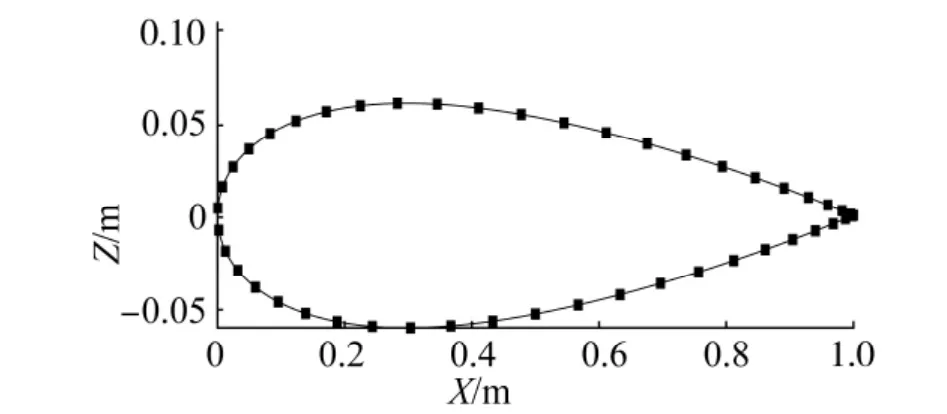
图2 NACA0012机翼剖面图Fig.2 Cutaway view for NACA0012 airfoil

由于机翼在首尾部的曲率较大，所以单元格之间的X轴距离不能是均匀的，否则计算结果会出现较大误差，因此采用余弦划分的方法，使网格在翼端处比较密集，在翼身处比较稀疏.图3(a)是当攻角为4°时，本文计算的二维NACA0012机翼表面压力分布Cp和文献［10］中相应数据的对比;图3(b)是当攻角为10°时，本文计算的二维NACA0012机翼表面压力分布Cp和CFD软件计算值的对比.

由图3可以看出本文的计算值与文献值和CFD计算值都符合得很好，故本文的计算方法具有很高的准确性和可靠性，可推广用于常规单体和三体船型的相应水动力及其导数的计算，具有很好的工程应用价值.

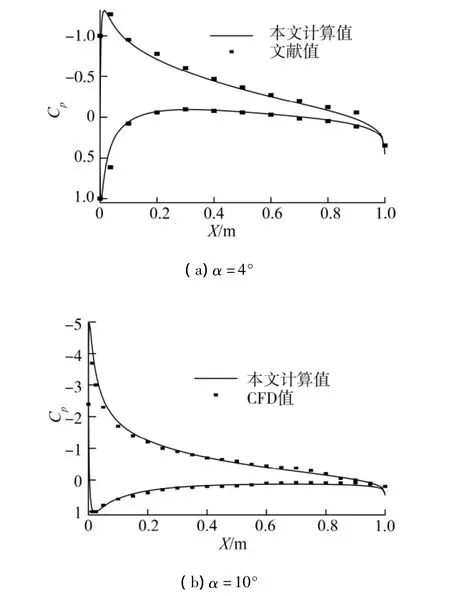
图3 本文Cp计算值和CFD值对比Fig.3 Numerical value vs CFD value for Cp

2.2 算例2

选取Wigley单体船型为第二算例2以进一步验证上述方法求解船舶操纵性水动力导数的有效性.船型函数表达式为

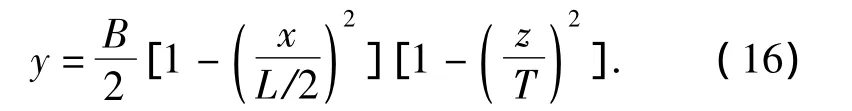
式中:L为水线长，B是水线宽，T为吃水深度，从便于数据对比和验证着想，算例船模规格与文献［9］完全一致，具体尺度为L=1 m，B=0.06 m，d= 0.05 m.假定来流速度大小为1 m/s，漂角分别取为－12°，－9°，－5°，0°，5°，9°，12°.根据表面流场求得船体表面的压力分布后，计算出作用在船模上的横向力Y和转首力矩A，将横向力和转首力矩无因次化:

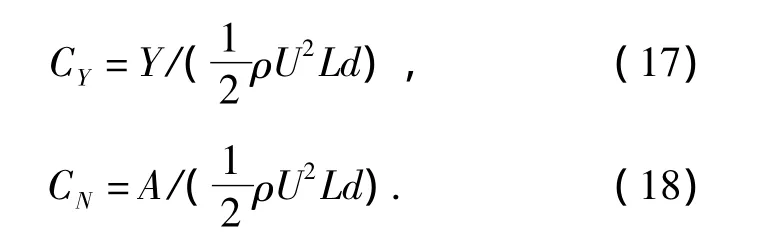
将本文计算的横向力系数CY和转首力矩系数CN随漂角的变化曲线，同井上公式［12］的估算值、文献［9］的计算值以及该文献中的试验值进行对比，如图4所示.横坐标代表漂角的大小β.由图中可以看出，本文计算的CY值和CN值与其他3种来源的数值比较吻合，特别是在漂角较小的情况下(β= 5°)，本文计算CY值与实验值相差13.4%，而文献［9］的计算值与试验值相差20%;本文计算CN值与实验值相差12.8%，而文献［9］的计算值与试验值相差15.3%.

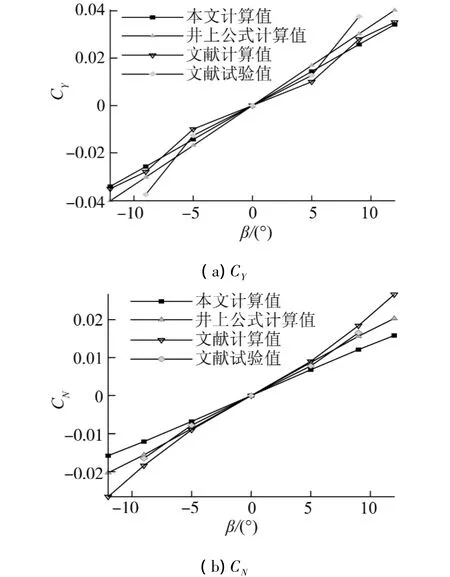
图4 随漂角变化的对比Fig.4 Curves of CY，CNvs drift angle

随着漂角的增大，本文计算值与试验值的差距有加大的趋势.在β=9°时，本文计算CY值与实验值相差31.3%，文献［9］的计算CY值与试验值相差25.5%，而本文计算CN值与实验值相差26.7%，文献［9］的计算CN值与试验值相差12.1%.可以看出文献［9］的计算值与试验值的差距比本文计算值与试验值的差值小，这是因为文献［9］的计算方法考虑了兴波的影响，在原理上说就计入了大漂角下的部分非线性影响，这可能是其与试验值符合好一些的主要原因之一.当然，实验本身的离散性和随机性，也对最终结果产生影响，但所关心的常用水动力导数本身就是小漂角情况下，忽略兴波的线性估算值，所以在估算Yv和Nv等水动力导数时可以暂时不考虑非线性因素的影响.综上所述，本文的计算值具有很高的可信度，且数值计算过程较计入自由面非线性兴波影响的简单，对计算机硬件资源要求较为节省.算例2进一步证明本文的方法在计算和分析船舶操纵性水动力时是有效的.

3 三体船斜航下横向力(矩)及其水动力导数计算

3.1 计算船型和网格划分

将上述数值方法推广用于三体船相应的操纵性水动力及其导数计算.三体船片体仍取为Wigley数学船型，计算模型规格如表1.

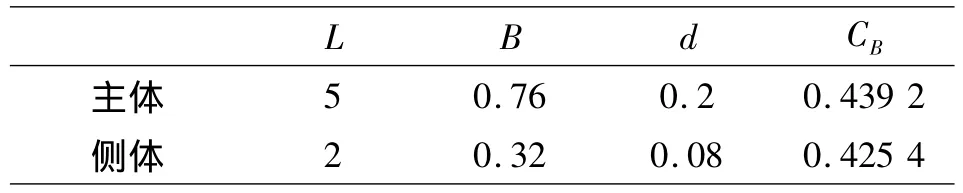
表1 三体船模几何参数Table 1 Parameters of Trimaran model m

由于船首尾和船底处船体表面曲率变化较大，所以将该船模主船体的水线按余弦分为100份，将吃水深度也按余弦分为5份;同样将侧体水线按余弦分为40份，将吃水深度按余弦分为3份，则将船体表面划分为1 480个网格，这样划分网格可以减小误差，提高计算的精度，具体网格如图5所示.

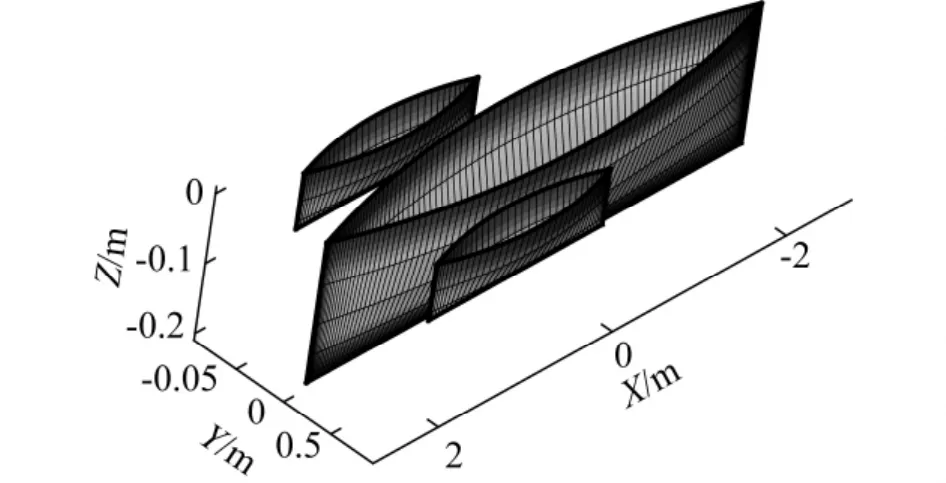
图5 船体表面网格Fig.5 Grids of ship surface

假设来流大小为1 m/s，侧体位置按下列方式选取:横向位置为p=0.6、0.7、0.8、0.9、1.0 m，纵向位置为 a=－1.5、－1.0、－0.5、0、0.5、1.0、1.5 m.

3.2 计算结果及分析

图6(a)和(b)表示的是水动力导数Yv和Nv随着侧体位置a，p的变化曲线.对计算结果作分析如下:

1)侧体横向位置对横向力的影响:三体船受到的横向力随着横向位置的增加而增加，但是这种增加的趋势随着横向位置的增加而减小.可见，随着横向位置的增加，主侧体之间的流场干扰减小，使三体船的横向力逐渐接近主侧体单独所受横向力之和，此时横向力是最大的;而计入主侧体流场干扰，将使横向力减小.试从绕船体的流动现象分析，造成这种现象的原因是，三体船背流面(Y正方向)的片体在迎流面片体(Y负方向)的流动阴影中，于是三片体组合体的总横向力(相当于组合体总升力)是减小的，这种影响与螺旋桨多叶片的叶栅作用对其升力影响类似;从这个角度考虑，也不难理解侧体位置靠前，横向位置的“动力阴影”或“叶栅效应”影响更大，图中也明确反映了这种趋势.

2)侧体纵向位置对横向力的影响:随着侧体越往船尾移动，三体船受到的横向力越大，而这种变化率在主船体首尾端区域较小，在主船体中区域较大.本文采用的是Wigley船型，侧体在船中区域时离主体物面比较近，受“动力阴影”或“叶栅效应”影响的片体体积和面积也较大，故相互干扰较大，进而使得横向力在该区域变化较快.

3)侧体横向位置对转首力矩的影响:三体船受到的转首力矩随着横向位置的增加而单调增大，但是变化率随着侧体横向位置的增加而逐渐减小，其变化趋势与横向力随横向间距变化趋势一致，显然是横向力受片体水动力干扰而变化引起的.

4)侧体纵向位置对转首力矩的影响:随着侧体往船尾的位置移动，三体船受到的转首力矩逐渐减小，且这种变化接近为线性规律，这表明侧体位置对转首力矩的影响主要来自侧体位置变化引起的转首力矩力臂的变化，其影响强度大于主侧体流场干扰的影响强度.

上述对图6中操纵性水动力导数Yv和Nv随a，p变化规律的特性分析，与物理概念、物理意义和物理直观都是一致的，在目前国内外都未见三体船操纵性水动力导数试验资料发表的情况下，上述数值计算结果规律的正确性在相当大的程度上验证了该方法对高速三体船的适用性和工程应用前景.当然，要确切地验证该方法对高速三体船操纵性水动力计算的适用性和计算精度，需加强开展高速三体船操纵性水动力的模型试验研究，并对更多的高速三体船算例按本方法实施数值计算，作者正在开展这方面的研究工作.

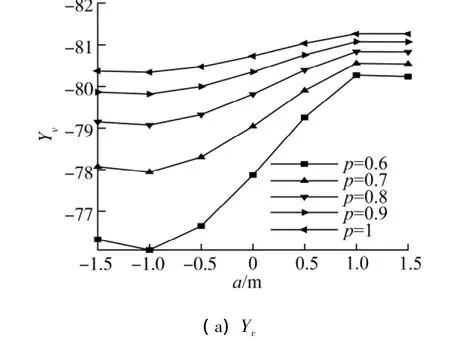
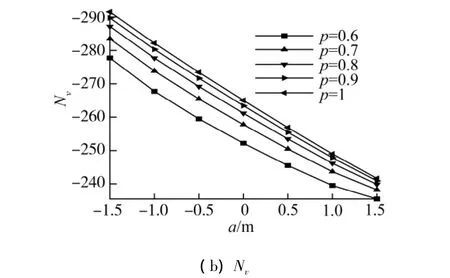
图6 随侧体位置变化曲线Fig.6 Curves of Yvand Nvvs outriggers’position

4 结论

本文研究和实现了三体船操纵性水动力(横向力及其力矩)的三维表面涡格法计算，并据所得计算结果分析了三体船侧体位置对操纵运动水动力(横向力及其力矩)特性的影响，综合本文的研究可以得出:

1)给出的三体船操纵性横向力和力矩三维表面涡格数值算法具有较高的准确性和可靠性，为三体船操纵运动水动力预报和操纵运动特性分析奠定了基础，具有很好的工程应用价值和前景.

2)三体船的侧体位置布局对三体船的操纵性横向力和转首力矩具有较大影响，对横向力的影响主要来自片体间流场水动力干扰，对转首力矩影响的主要来自侧体位置对转首力矩力臂的影响，片体间流场水动力干扰亦起一定作用.

3)侧体位置的靠前放置能使三体船获得较大的转首力矩，从而使三体船的航向稳定性降低，回转性增加，因此如需增加三体船的航向稳定性，应该将侧体靠后放置.

4)侧体横向间距增大，受片体间水动力干扰影响，横向力呈减小趋势.

在三体船设计和建造时，必须考虑上述对其操纵性水动力影响的因素，根据实际需求和用途进行分析和研究，合理地布置三体船侧体位置，使其操纵性能达到预期目标.

［1］韩开佳，黄德波.三体船的兴波阻力计算［J］.哈尔滨工程大学学报，2000，21(1):6-10.

HAN Kaijia，HUANG Debo.Resistance calculation of tramaran［J］.Journal of Harbin Engineering University，2000，21(1):6-10.

［2］卢晓平.高速三体船兴波阻力和片体布局优化［J］.水动力研究与进展A辑，2004，19(3):347-354.

LU Xiaoping.Research of high-speed trimaran’s wave resistance and outriggers’displacement optimization［J］.Journal of Hydrodynamics Ser A，2004，19(3):347-354.

［3］卢晓平.不同布局高性能船的阻力对比分析［J］.水动力研究与进展B辑，2005，20(3):322-330.

LU Xiaoping.The comparison of the resistance for several displacement high performance vehicles［J］.Journal of Hydrodynamics Ser B，2005，20(3):322-330.

［4］卢晓平.高速三体船研究综述［J］.海军工程大学学报，2005，17(2):101-108.

LU Xiaoping.Research summary of high speed trimaran［J］.Journal of Naval University of Engineering，2005，17 (2):101-108.

［5］LUCA S，ROBERT D，MICHELE V，et al.Design project of a tramaran multipurpose frigate—study of the hydrodynamic aspects［C］//Proc of the 7th International Conference on Fast Sea Transportation FAST.Naples，Italy，2003.

［6］KANG Kunjin，KIM Sunyong，CHOI Y R.Seakeeping and maneuvering performances of the 2500 tons class trimaran［C］//IWSH’2001.Wuhan，China，2001.

［7］卢晓平.三体船操纵性计算和特性分析［J］.海军工程大学学报，2009，21(1):47-53.

LU Xiaoping.Trimaran’s maneuverability calculation and characteristic analysis［J］.Journal of Naval University of Engineering，2009，21(1):47-53.

［8］姚迪.三体船水动力导数计算和操纵性能研究［J］.海军工程大学学报，2008，20(12):78-83.

YAO Di.Trimaran’s hydrodanamic coefficient calculation and manoeuverability emulation research［J］.Journal of Naval University of Engineering，2008，20(12):78-83.

［9］吴秀恒.船舶操纵性［M］.北京:国防工业出版社，2004: 45-59.

［10］苏玉民，黄胜.船舶螺旋桨理论［M］.哈尔滨:哈尔滨工程大学出版社，2003:159-180.

［11］王献孚.船舶计算流体力学［M］.上海:上海交通大学出版社，1992:101-151.

［12］姚迪.三体船水动力导数计算与操纵特性仿真研究［D］.武汉:海军工程大学，2008:19-38.

YAO Di.Theoretical calculation of hydrodynamic derivatives for trimaran and manoeuverability feature numerical emulation of trimaran［D］.Wuhan:Nav University of Engineering，2008:19-38.