船舶螺旋桨流固耦合稳态求解算法
张帅,朱锡,侯海量
(海军工程大学 船舶与动力工程学院,湖北 武汉 430033)
水面舰艇螺旋桨大多采用锰-镍-铝-铜或镍-铝-青铜合金制成.尽管合金材料具有屈服强度高和可靠性好等优势,但加工成螺旋桨几何形状的难度较高,且金属螺旋桨较差的声学性能使得其极易因振动而产生噪声.而纤维增强复合材料具有比强度高、耐腐蚀性好、良好的阻尼特性以及材料可设计性强等优点.因此复合材料应用于舰船螺旋桨和潜艇推进系统中[1]将改善螺旋桨的综合性能.但不同于金属螺旋桨,复合材料螺旋桨在水动力作用下会产生大的变形,其水动力性能必然发生变化.因此要得到复合材料螺旋桨的水动力性能,螺旋桨的流-固耦合算法是基础.传统的螺旋桨理论设计与计算建立在势流理论基础之上,未能全面考虑粘性的影响且不考虑旋度,因而无法准确预测桨叶边界层、螺旋桨尾流场的结构及桨叶梢涡的形成等真实情况下的流动特性[2].基于RANS方程的粘性流场计算螺旋桨的流场特性的方法日趋完善,黄胜等[3-5]等分析了螺旋桨在不同工作状态下的水动力性能.关于螺旋桨流-固耦合算法的研究,LIN H J等[6]采用升力面法和九节点退化壳单元耦合算法,实现了求解复合材料螺旋桨的水动力性能的算法.Young Y L[7]研究了面元法和软件ABAQUS耦合的螺旋桨流-固耦合计算方法,但这些方法均是基于势流理论的螺旋桨水动力计算.
本文首先通过不同湍流模型和试验,验证求解螺旋桨的敞水性能,再将粘性流场计算软件和有限元耦合起来,推导变形后螺旋桨的几何参数,实现螺旋桨流-固耦合的稳态求解算法.本文计算采用实验测得的复合材料板拉伸模量和泊松比,将复合材料考虑为各向同性,没有考虑复合材料的铺层结构.
1 数学模型
1.1 流体控制方程
考虑螺旋桨在粘性湍流中旋转,其连续性方程和动量方程可表示为:
连续方程:

动量方程:

RANS方程虽然不用求解流场中的瞬时量,但是方程却引入了新的未知量-雷诺应力,这时的方程解不封闭.要封闭求解方程,就必须引入新的方程,这些方程通过各种湍流模型来定义.
1.2 湍流模型的选取
为使RANS方程封闭,将雷诺应力用低阶或时均量表达,即湍流模型.封闭RANS方程主要有REYNOLDS应力方程模型(RSM)与涡粘模型2种.涡粘模型以湍流各向同性为基础,认为雷诺应力和时均速度呈线性关系,该类模型求解简单,计算容易收敛.涡粘模型应用较广泛的有κ-ε,RANG κ-ε模型和SST κ-ω模型.而RSM模型以湍流各向异性为基础,考虑雷诺应力的对流和扩散作用,直接寻找雷诺应力的输运方程.本文通过比较分析几种常用湍流控模型,通过求解时间和求解精度方面的对比以及考虑到流固耦合本身对计算机性能的要求等方面进行综合考虑.螺旋桨水动力性能计算模型选择SST κ-ω湍流模型.该模型是利用混合函数将κ-ε和κ-ω2方程相结合而构建的湍流模型,在近壁区采用κ-ω方程,其他区域则采用κ-ε方程以获得湍流粘性作用,考虑了κ-ω方程近壁区模拟时的有效性及远场区无法准确模拟的不足[8].最终选择SST κω模型求解螺旋桨的流固耦合特性.
1.3 计算方法
计算螺旋桨流场的控制方程是一系列非线性偏微分数学物理方程,需借助数值方法对其进行求解.本文利用Ansys/cfx软件完成该数值计算.收敛判据设定为0.000 1.计算区域分为内、外2个流域,在内流场建立一个固定于螺旋桨的旋转坐标系,采用MRF坐标系模型对螺旋桨周围的旋转流场进行计算,外围流场则在绝对静止坐标系下进行求解.将进口边界设置为速度入口条件,给定均匀来流的速度分量;出口边界给定静压分布,外边界设为开放界面;考虑粘性影响,螺旋桨表面定义为不可滑移壁面.
2 流体计算模型
文中采用DTMB4119螺旋桨,它是一种无侧斜无后倾分布的三叶螺旋桨,被ITTC选为验证数值方法预报精度的标准模型.桨叶直径为0.304 8 m,盘面比为0.6,桨叶剖面为NACA-66(mod)型,毂径比为0.2,螺距比(0.7R)为1.084.文中采用Excel编制计算过程文件,计算出螺旋桨叶面和叶背各个半径处的型值点,将计算出的型值点转换为文本文件,然后导入SolidWorks软件中,建立三维实体螺旋桨模型.螺旋桨几何模型和坐标如图1所示.坐标轴的定义为:x轴与螺旋桨的旋转轴一致,指向下游;y轴与桨叶参考线一致;z轴符合右手法则.计算采用全尺寸模型,转速为n=10 r/s和20 r/s,通过改变来流速度来实现不同的进速系数.
网格质量直接决定计算的收敛性、效率和精度,因此,应根据流场中各物理量的分布特点对计算域进行合理的网格划分[1].

图1 4119桨几何模型Fig.1 Geometry of propeller 4119
将求解域分成旋转区和静止区2个区,采用非结构网格划分方法,2个区采用CFX的GGI方式连接.即首先在螺旋桨表面生成三角形网格,再通过值要控制在30~300,通过多次试算确定表面网格大小和桨叶边界层的过渡方式和层数.螺旋桨表面网格和壁面棱柱过渡层网格如图2所示.总网格数为120×104.
3 结构模型
通过流体计算软件求出螺旋桨的水动力载荷以后通过Ansys-cfx软件指定流固耦合界面将流体压力通过表面效应单元的方式传递给有限元单元.因流体计算和结构计算采用的是非同种单元类型,为保证求解精度和数据传递的准确性,在划分有限元网格时保证导边和随边以及叶梢附近的网格要密一些.经多次试算后的有限元网格如图3所示.考虑到螺旋桨自身质量和运转工况,在ANSYS中设置旋转轴和施加旋转速度即可施加离心力和重力作用,桨叶根部边界为固支端.计算模型采用的材料参数如表1所示,其中S玻璃纤维为实验所测板拉结果,计算出的铝青铜材料桨叶的变形比S玻纤桨叶变形低一个数量级,因此主要考虑高强S玻纤的桨叶结构.计算用复合材料桨几何和金属桨几何相同.

图3 桨叶有限元计算模型Fig.3 Finite element model of the blade

表1 桨叶材料参数Table 1 Properties of the materials
4 螺旋桨敞水性能计算和验证
对于流体动力载荷,由于桨叶工作于复杂的流场中,叶面和叶背受到分布载荷,这种载荷既不均匀,也不满足一些简单规律,因此如何尽可能真实地模拟桨叶的载荷分布是流固耦合分析的关键所在.
4.1 螺旋桨敞水性能计算和对比
为了实现结构载荷计算的准确性,首先采用几种常用的湍流模型(κ-ε,SST κ-ω和RSM)对比求解螺旋桨的水动力敞水性能并和JESSUP S D[9]实验结果进行了对比.
对比结果如图4、5所示,螺旋桨敞水动力参数的计算值和实验结果吻合较好,计算所得的KT和10KQ与实验结果的最大误差除了κ-ε模型为12.5%以外,SSTκ-ω为9.6%和RSM为8%,而对于螺旋桨效率的计算值仅有κ-ε模型超过了11.5%,而其他情况误差均在5%.需要指出的是,最大误差值均出现于最大进速情况.原因在于相同转速和相同直径下,进速越大,相应的推力和扭矩越小,任何一个干扰就会导致预测值和实验值的误差增加很大.整体来看SSTκ-ω模型和RSM模型均能得到精度较高的计算结果.图6为在同台计算机上不同湍流模型在不同进速下的计算时间对比图.由图6可知,相同进速下RSM模型的求解时间最长,在低进速时尤为明显,κ-ε求解时间最短,而SSTκ-ω模型求解时间接近κ-ε模型.
从以上对比可知,SSTκ-ω模型可以在保证求解精度的情况下,求解时间减少很多.另考虑到流固耦合计算本身对计算机求解性能和求解时间的严格要求,综合考虑,螺旋桨流体计算湍流模型采用SSTκω模型.

图4 计算KT和10KQ与实验结果的对比Fig.4 Comparisons of calculated and experimental KT and 10 KQ

图5 计算效率ETA和实验结果对比Fig.5 Comparisons of calculated and experimental ETA
4.2 螺旋桨表面压力分布对比
图7为螺旋桨在设计工况J=0.833时,r/R= 0.3、0.7和0.9半径上JESSUP S D实验换算得到的弦向压力分布和采用SSTκ-ω计算值的比较.
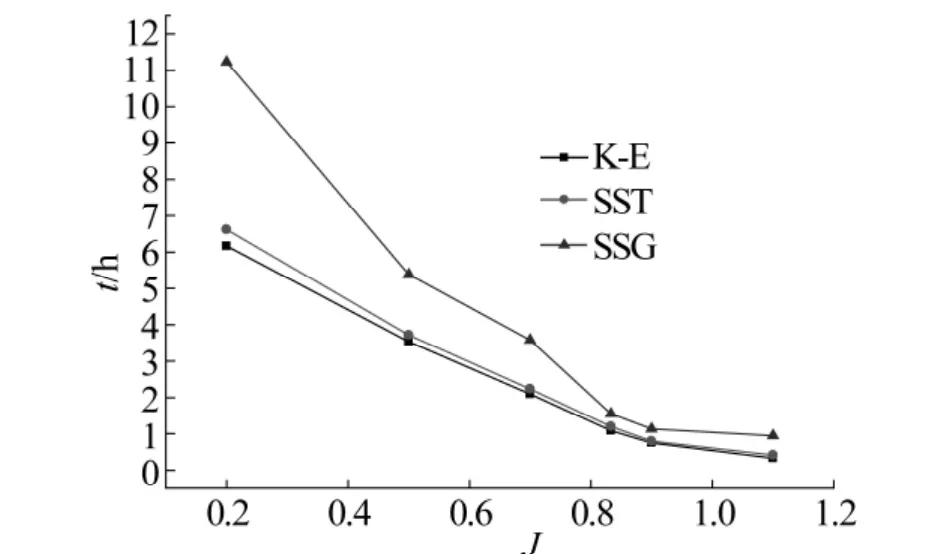
图6 求解时间对比(n=10r/s)Fig.6 Comparisons of calculated durations(n=10 r/s)

图7 叶切面压力分布系数Fig.7 Comparisons of pressure coefficient
5 变形后桨叶几何参数的推导
桨叶参考线即叶剖面鼻尾线中点的坐标:[10]

设导边的坐标为(xl,r,θl)或(xl,yl,zl),随边的坐标为(xt,r,θt)或(xt,yt,zt),叶宽(即弦长)分布为C(r),则桨叶的轮廓线可表示:

式中:C(r)为叶剖面弦长;φ(r)为叶剖面螺距角;下标l、t分别表示导边(取-)和随边(取+).
选择无量纲弦长s,导边表示为0,随边表示为1,桨叶弦向中点为1/2,桨叶剖面的拱度和厚度分布分别表示为f(s)和t(s),桨叶拱弧面的表达式为:

式中:下标c表示为拱弧面;δk=2π(k-1)/K,k= 1,2…,K,为桨叶数.

变形后各叶切面半径为rref:



在推导式(9)的过程中,由于螺旋桨的变形量很小,所以认为C(r)不变.将和代入式(4)就可得到变形后的纵倾(r).最后将所有变形后的节点坐标代入到式(5)桨叶拱弧面的方程中,就可得到变形后的拱弧f'(s)

6 螺旋桨流固耦合算法的实现
复合材料螺旋桨桨叶受到水动力载荷和离心力的作用,会产生较大的变形,那么桨叶结构的离散方程为

式中:K为桨叶刚度矩阵,u桨叶节点位移矢量矩阵,F为桨叶所受外载荷矩阵.而式(11)中位移矢量矩阵u需采用有限元软件计算,而F求解需要流体计算软件.两者求解的平衡实现需借助流固耦合算法.因此设计了一种求解螺旋桨性能的流固耦合算法,求解流程如图8所示.

图8 流固耦合的算法求解流程图Fig.8 Flow chart of computation algorithm of FSI
计算采用稳态求解,不考虑瞬时效应.详细求解过程为:
1)通过第2节中的方法建立螺旋桨的流体计算模型,计算出螺旋桨的敞水性能和压力分布.
2)将1)计算的压力载荷结果通过流固耦合界面的方法传递给第3节中建立的有限元模型,计算出螺旋桨的变形,将变形后的桨叶节点坐标输出到文本文件.
3)采用第5节中的方法确定变形后的螺旋桨几何参数,建立变形后的螺旋桨几何模型.
4)将变形后的几何再次输入到CFD软件中求解螺旋桨的敞水性能和压力分布.
5)判断是否满足平衡方程和收敛条件,如果满足则输出计算结果,包括结构变形量、应力场、推力、扭矩以及推进效率等.如不满足收敛条件,重复迭代2)、3)、4)步,直至结果收敛.
文中指定的收敛准则为2个迭代步内的推力系数和扭矩系数小于2%.计算过程一般迭代2次就可达到收敛.
7 应力、变形计算及变形后的压力分布
7.1 应力水平和变形分布
图9是不同转速、不同进速下的MISE应力分布和变形对照图(变形均放大20倍).设计工况,n=10 r/s和 20 r/s时,最大等效应力分别为2.3 MPa和8.62 MPa.由图可以看出,相同转速不同进速情况下,低进速情况下的MISE应力比高进速下的要大.不同转速,相同进速情况,转速高的应力要比转速低的要大.最大MISE应力分布均在叶根弦向中心位置.根据螺旋桨理论可知,相同转速下,在低进速时为螺旋桨的“重载”状态,推力和扭矩均较大;高进速时为“轻载”状态,推力和扭矩较小,所以在低进速时螺旋桨的变形要比高进速的大,应力分布也是一致的.相同进速,不同转速下,根据螺旋桨的无因次理论,推力和扭矩增大数为2的转速倍数次方.弹性范围应力和变形也增加同样倍数.
图10和图11是不同转速、进速下的桨叶变形分布.从图10可以看出,桨叶变形引起了桨叶侧斜的改变.4119螺旋桨为无侧斜桨,变形后侧斜角为正值,即向随边倾斜.相同转速时,低进速的侧斜改变比高进速的大,这与前面分析的受力规律一致.
而图11则显示了在水动力载荷的作用下,桨叶朝着船体方向变形,且在叶稍附近达到最大值,变形规律类似悬臂梁.变形后的桨叶剖面鼻尾线在螺旋桨轴向(x轴)方向的投影有零变为正值,即导致产生了纵倾的分布.另桨叶朝着船体方向变形,促使各半径处的螺距角分布改变.即在随边附件变形大,导致螺旋桨桨叶螺距的变小.

图9 不同转速n、进速J下的MISE应力分布Fig.9 MISE stress distribution at different n and J

图10 侧斜的改变(线框为未变形,实体为变形后)Fig.10 Changes of the blade skew

图11 纵倾的改变(线框为未变形,实体为变形后)Fig.11 Changes of the blade rake
7.2 变形前、后桨叶的压力分布
图12为设计进速J=0.833时变形前后桨叶压力面和吸力面的压力分布对比图.如图12所示,变形的叶稍改变了叶稍附近压力的分布.变形后正压力峰值相应减小,负压力峰值相对升高.

图12 J=0.833螺旋桨变形前后压力分布(n=10 r/s)Fig.12 Predicted pressure distribution of 4119 in the undefand def-configuration,J=0.833,n=10 r/s
8 结论
1)对螺旋桨进行稳态流固耦合分析,SST κ-ω湍流模型预报精度高且求解时间合理.
2)实现了螺旋桨的流固耦合算法,可以求解桨叶的变形和应力分布及变形后的推进性能.
3)螺旋桨在水动力作用下产生的变形,改变了螺旋桨的初始几何参数,因此改变了螺旋桨的压力分布,从而改变了螺旋桨的水动力性能.对于易于变形的复合材料螺旋桨设计、计算,要考虑桨叶变形的影响.
[1]MOURITZ A,GELLERT E,BURCHILL P,et al.Review of advanced composite structures for naval ships and submarines[J].Composite Structures,2001,53:21-41.
[2]高富东,潘存云,蔡汶珊,等.基于CFD的螺旋桨敞水性能数值分析与验证[J].机械工程学报,2010,46(8): 133-139.
GAO Fudong,PAN Cunyun,CAI Wenshan,et al.Numerical analysis and validation of propeller open-water performance based on CFD[J].Journal of Mechanical Engineering,2010,46(8):133-139.
[3]黄胜,王超,王诗洋.不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J].哈尔滨工程大学学报,2009,30(5):484-485.
HUANG Sheng,WANG Chao,WANG Shiyang.Application and comparison of different turbulence models in the computation of a propeller’s hydrodynamic performance[J]Journal of Harbin Engineering University,2009,30(5): 484-485.
[4]沈海龙,苏玉民.基于滑移网格技术的船桨相互干扰研究[J].哈尔滨工程大学学报,2010,31(1):1-7.
SHEN Hailong,SU Yumin.Use of the sliding mesh technique to analyze interaction between ship hulls and propellers[J].Journal of Harbin Engineering University,2010,31 (1):1-7.
[5]王超,黄胜,单铁兵.基于多块混合网格方法预报螺旋桨非正常工作状态时的水动力性能[J].船舶力学,2010,14(1/2):51-55.
WANG Chao,HUANG Sheng,SHAN Tiebing.Computations of the propeller’s hydrodynamic performance in abnormal working condition based on multi-block meshes[J].Journal of Ship Mechanics,2010,14(1/2):51-55.
[6]LIN H J,LIN J J.Nonlinear hydro-elastic behavior of propellers using a finite-element method and lifting surface theory[J].Journal of Marine Science and Technology,1996,1:114-124.
[7]YOUNG Y L.Fluid-structure interaction analysis of flexible composite marine propellers[J].Journal of Fluids and Structures,2008,24:799-818.
[8]李巍,王国强,汪蕾.螺旋桨粘流水动力特性数值模拟[J].上海交通大学学报,2007,41(7):1200-1203.
LI Wei,WANG Guoqiang,WANG Lei.The numerical simulation of hydrodynamics characteristic in propeller[J].Journal of Shanghai Jiaotong University,2007,41(7):1200-1203.
[9]JESSUP S D.An experimental investigation of viscous aspects of propeller[D].Washington DC:The Catholic University of America,1989:65-154.
[10]王国强,董世汤.船舶螺旋桨理论与应用[M].哈尔滨:哈尔滨工程大学出版社,2007:89-94,113-114.

