两个矩阵Fan积和Hadamard积的特征值的界

杨晓英，刘 新

（四川信息职业技术学院 基础教育部，四川 广元 628017）

两个矩阵Fan积和Hadamard积的特征值的界

杨晓英，刘 新

（四川信息职业技术学院 基础教育部，四川 广元 628017）

关于非奇异M-矩阵A与B的Fan积A*B，给出A*B的最小特征值τ（A*B）下界的新估计式，同时也给出非负矩阵A与B的Hadamard积AB的谱半径ρ（AB）上界的新估计式，这些估计式只与矩阵的元素有关，易于计算．数值算例也说明所得估计式改进了现有的结果．

M-矩阵；非负矩阵；Fan积；Hadamard积；最小特征值；谱半径

1 预备知识

N表示集合{1，2，…，n}．Rm×n表示m×n阶实矩阵．Cm×n表示m×n阶复矩阵．ρ（P）表示n×n阶非负矩阵P的谱半径．

定义1.1 设A=（aij）∈Rn×n，如果aij≥0（i，j=1，2，…，n），则称矩阵A为非负矩阵，记为A≥0；若aij＞0（i，j=1，2，…，n），则称矩阵A为正矩阵，记为A＞0．

其中A11是r×r阶子矩阵，A22是（n-r）×（n-r）阶子矩阵（1≤r＜n），则称矩阵A为可约矩阵．若没有置换矩阵P存在，则称矩阵A为不可约矩阵．

定义1.3 设A=（aij）∈Rn×n，且aij≤0，i≠j，则称矩阵A为Z矩阵（简记为A∈Zn×n）．

定义1.4 设A=（aij）∈Zn×n，A可以表示为A=λI-B，其中B≥0，当λ≥ρ（B）时，则称A为M-矩阵．特别地，当λ＞ρ（B）时，称A为非奇异M-矩阵；当λ=ρ（B）时，称A为奇异M-矩阵．

定义1.5 对于A=（aij）∈Zn×n，记τ（A）=min{Re（λ）：λ∈б（A）} ， （其中б（A）表示矩阵A的谱）， τ（A）称为A的最小特征值．

在定义1.5的基础上，有如下基本的事实［1］：

（ⅰ） 如果A，B∈Zn×n，且A≥B，则 τ（A）≥ τ（B） ；

定义1.6 设称为矩阵A与B的Fan积．

如果A，B∈Zn×n是M-矩阵，则A*B也是M-矩阵［2］．

在文献［1］中，给出了关于τ（A*B）的一个下界估计式：若A，B是M-矩阵，则

τ（A*B）≥τ（A）τ（B）.

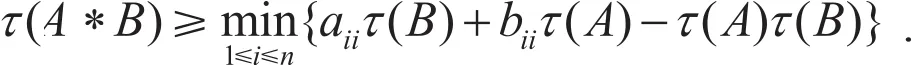
2009 年，Liu等在文献［5］中给出τ（A*B）的一个新的下界估计式：

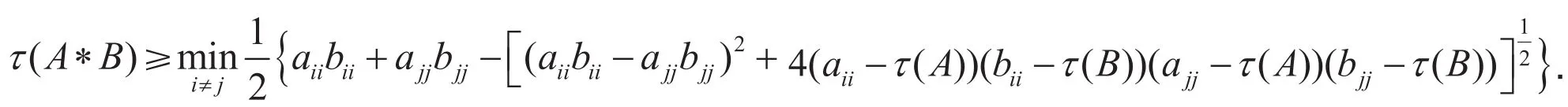
2010 年，Li等在文献［6］中给出一个只依赖于矩阵元素的新估计式：

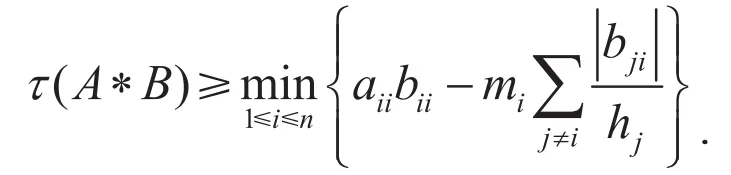
本文将在第二部分给出非奇异M-矩阵A，B的新的τ（A*B）下界的估计式．

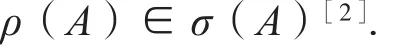
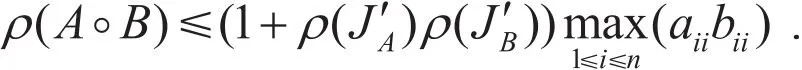
2009 年，Liu等在文献［5］中得出下面的结论：

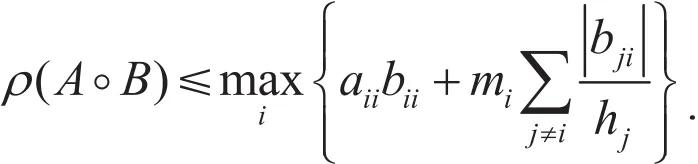
2 非奇异M-矩阵Fan积的最小特征值下界的估计

引理2.1［7］设A=（aij）∈Cn×n，0≤α≤1，且x1，x2，…，xn是正实数．则矩阵A的特征值位于下列区域之中

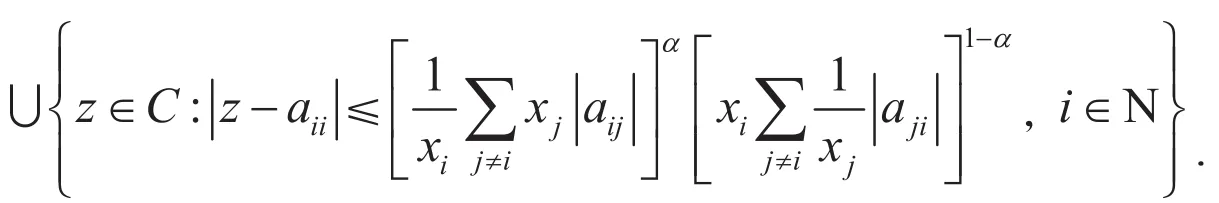
引理2.2［7］设A=（aij）∈Cn×n，0≤α≤1，且x1，x2，…，xn是正实数．则矩阵A的特征值位于下列区域之中

定理2.1 设 A=（aij）∈Rn×n，B=（bij）∈Rn×n，是非奇异M-矩阵，则

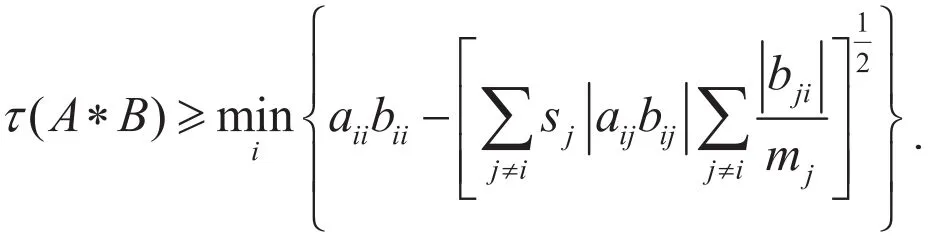
证明：若A*B不可约，则A，B不可约．设λ是A*B的特征值且满足τ（A*B）=λ.由引理2.1知，存在i（1≤i≤n），使

若A*B可约，Zn中的矩阵是非奇异M-矩阵的充要条件是它的所有顺序主子式为正．令D=（dij）是n ×n阶置换矩阵，且d12=d23=…=dn-1，n，n=dn1=1，其余的dij=0，则对于任意正实数t，当t充分小时，使得A-tD，B-tD 的所有顺序主子式为正，从而A-tD和B-tD都是不可约非奇异M-矩阵，若用A-tD，B-tD代替A，B并令t→0，则结论仍然成立．

例2.1［6］设

由估计式τ（A*B）≥τ（A）τ（B）=0.191；

应用本文的定理2.1，得τ（A*B）≥2.4725．

事实上，τ（A*B）=3.2296 ．

注：通过例子的数值结果， 可知由定理 2.1的结果有效地改进现有的结果．

3 非负矩阵Hadamard积的谱半径上界的估计

引理3.1［8］设n阶矩阵A≥0，则下列结论之一成立

（1）A不可约；（2） 存在置换矩阵P，使得

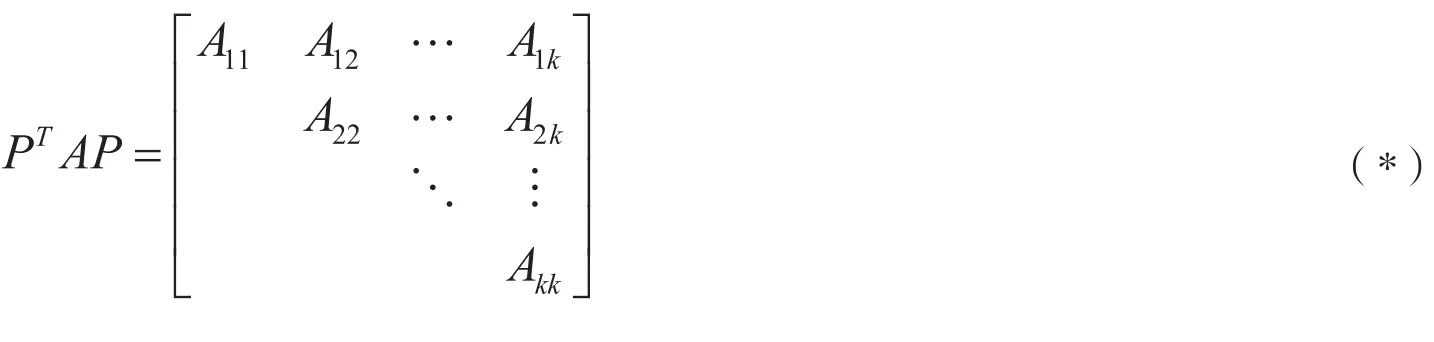
其中Aii，（i=1，2，…，n）或不可约，或为0．

引理3.2［8］设A∈Rn×n，如果A有形如（*）式的不可约标准形，则

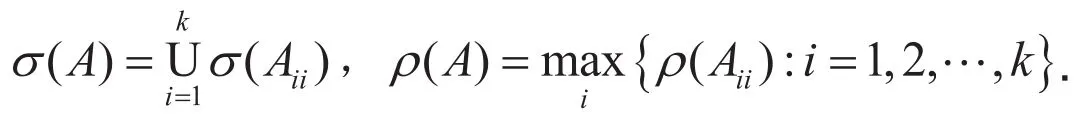
定理3.1 设A=（aij）∈Rn×n，B=（bij）∈Rn×n，且A，B≥0，则

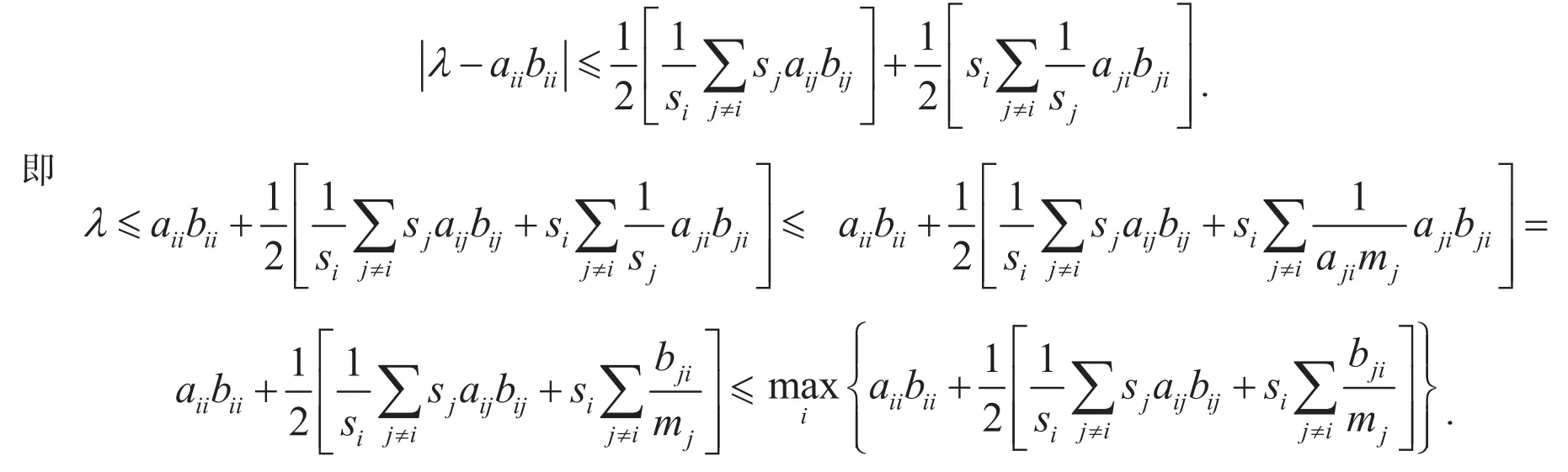
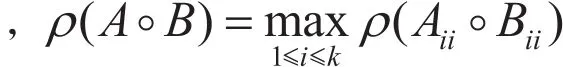
定理3.2 设 A=（aij）∈Rn×n，B=（bij）∈Rn×n，且A，B≥0，则

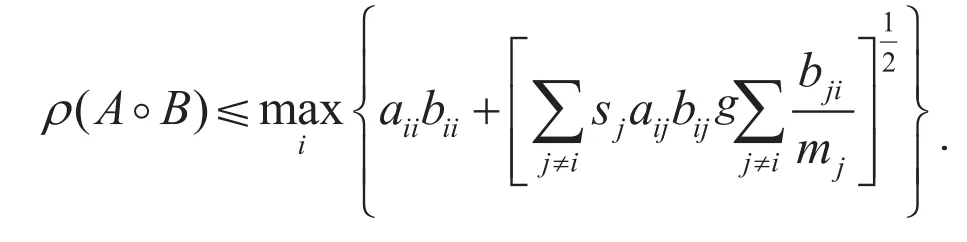
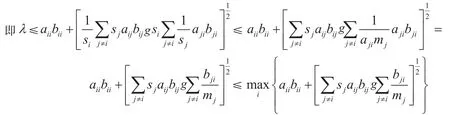
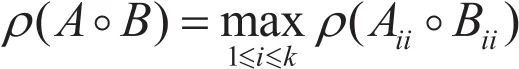
例3.1［6］设

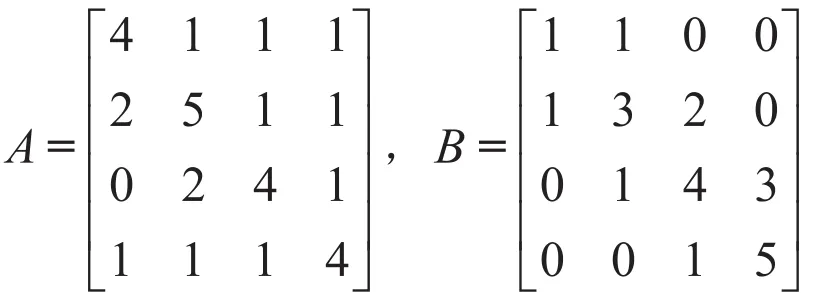
注：通过例子， 比较定理3.1、定理3.2的结果与其他相应的结果， 可以发现定理3.1和定理3.2提高了ρ（AB）的上界．

［1］ Horn R A， Johnson C R. Topics in matrix analysis［M］. New York： Cambridge University Press， 1991： 129， 131， 358-359.

［2］ 陈景良， 陈向晖. 特殊矩阵［M］. 北京： 清华大学出版社， 2000： 250， 449.

［3］ Fang M Z. Bounds on eigenvalues of the Hadamard product and the Fan product of matrices［J］. Linear Algebra Appl， 2007， 425： 7-15．

［4］ Huang R. Some inequalities for the Hadamard product and the Fan product of matrices［J］. Linear Algebra Appl， 2008， 428：1551-1559．

［5］ Liu Q B， Chen G L. On two inequalities for the Hadamard product and the Fan product of matrices［J］. Linear Algebra Appl，2009， 431： 974-984．

［6］ Li Y T， Li Y Y， Wang R W， et al. Some new bounds on eigenvalues of the Hadamard product and the Fan product of matrices［J］. Linear Algebra Appl， 2010， 432： 536-545.

［7］ 李艳艳， 李耀堂. 矩阵Hadamard积和Fan积的特征值界的估计［J］. 云南大学学报：自然科学版， 2010，（2）：125-129.

［8］ Berman A， Plemmons R J. Nonnegative Matrices in the Mathematical Sciences［M］. New York： Academic Press， 1979：26-27.

Bounds on Eigenvalues of the Fan Product and the Hadamard Product of Two M atrices

YANG Xiao-ying, LIU Xin
(Basic Education Department,Sichuan Information Technology Vocational College,Guangyuan 628017, China)

If A and B are nonsingular -matrices,a new lower bound on the m inimum eigenvalue for the Fan product of A and B and new upper bounds on the spectral radius of nonnegative matrces A and B are given in the paper. The bounds improve several existing results in some cases and the estimating formulas are easier to calculate for they only depend on the entries of matrices A and B.

Matrix; nonnegative matrix; Fan product; Hadamard product; m inimum eigenvalue; spectral radius

O151.21

： A

：1674-9200（2012）03-0031-05

（责任编辑 刘常福）

2012 - 05 - 04

杨晓英（1984 -），女，山西忻州人，四川信息职业技术学院基础教育部助教，硕士，主要从事矩阵理论方面的研究．