基于模糊PID的静变电源控制技术研究

樊波，牛江川，程培源，吴家梁

（空军工程大学导弹学院，陕西三原713800）

近年来，随着电力电子技术的发展，静变电源越来越广泛地应用于工业、军事、医疗、航空航天等领域。在某型地空导弹武器系统中，静变电源是主要的设备之一，是整个武器系统电能的来源，能否可靠不间断地供电直接影响武器系统性能的发挥。设计高性能变频电源是当前的趋势之一，静变电源的高性能主要表现在稳压性能好、输出电压波形质量高、负载适应性强、动态特性好等方面。为了获得高质量的正弦输出电压波形，人们将现代控制理论应用到静变电源系统的控制中，提出了很多基于调制策略的控制方法。

PID控制器结构简单,鲁棒性强，目前在很多方面都有着广泛的应用。但是随着科学技术的进步，被控对象变得越来越复杂，利用传统的PID控制器往往得不到较好的控制效果。为了改善常规PID的控制效果，增强系统的适应性，本文设计出一种调整系统控制量的模糊PID控制器，模糊控制对于克服系统的非线性、时变性具有一定的优势。本文结合静变电源控制系统的特点，采用模糊PID控制算法，提高了静变电源输出电压波形的质量，使系统兼具良好的动、静态性能。

1 模糊PID控制器的设计

1.1 传统PID控制原理与出现的问题

经典增量式PID 的控制算式为：

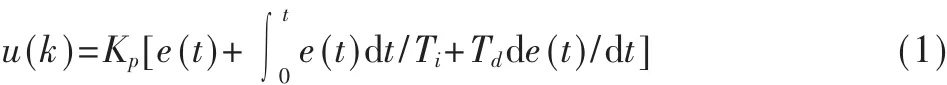
其中：Kp、Ti、Td分别为比例系数、积分时间常数、微分时间常数。也可将式（1）描述为：

式中KP、KI、KD分别为比例、微分、积分系数；f[·]是与KP、KI、KD、u(k-1)、y(k)等有关的非线性函数。

离散化后的PID控制算式为：

式中Δe(k)=e(k)-e(k-1)，采用增量式PID控制算法时，计算机输出的控制增量Δu(k)对应的是本次执行机构位置的增量。当计算机出现故障时，执行机构仍保持在前一步的位置上，使得系统的安全性与可靠性更高。对应实际的控制量，目前较多利用式（3）来完成。

增量式PID控制器参数一经确定后就不再改变，参数没有自适应环境变化的能力。然而，在实际工业生产过程中，静变电源的输出电压具有非线性、时变性和不确定性，而且所带负载常常发生变化，使得控制对象和模型失配，传统PID控制器参数往往优化不良，控制效果欠佳。为了克服传统PID控制系统的缺陷，引入了模糊控制与PID控制相结合的方法，以改善系统的跟踪效果，获得期望输出。

1.2 模糊PID控制策略

根据以往经验，静变电源输出电压波形质量与调制波信号密切相关，当输出电压波动很大时，如采用常规的PID控制器，其控制性能可能会变差甚至不稳定。因此，为了实现控制器的自适应能力，提出了基于模糊PID算法的静变电源的直接电压控制方法。

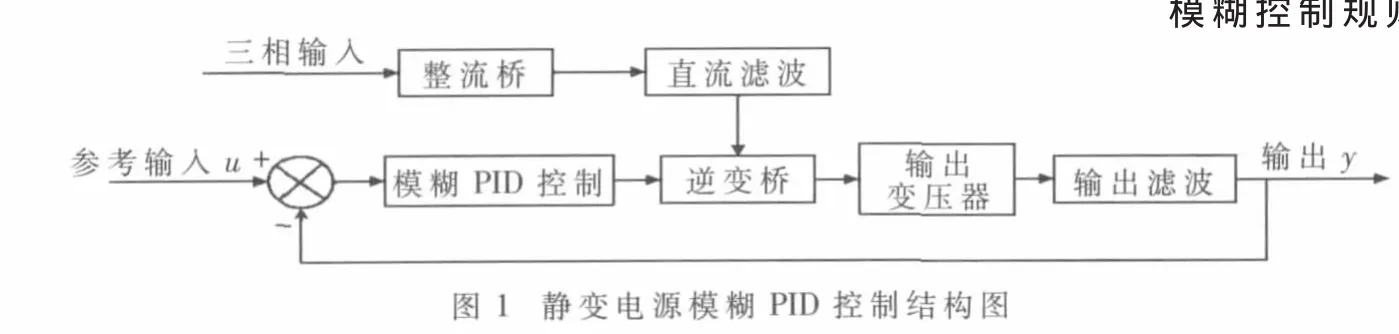
静变电源的模糊PID控制原理如图1所示，将期望值与实际输出值的误差信号经过模糊PID调节后，分析误差信号产生调制波，再经三角载波调制后生成PWM信号控制逆变桥，使系统输出信号逼近期望值，模糊PID控制原理如图2所示。

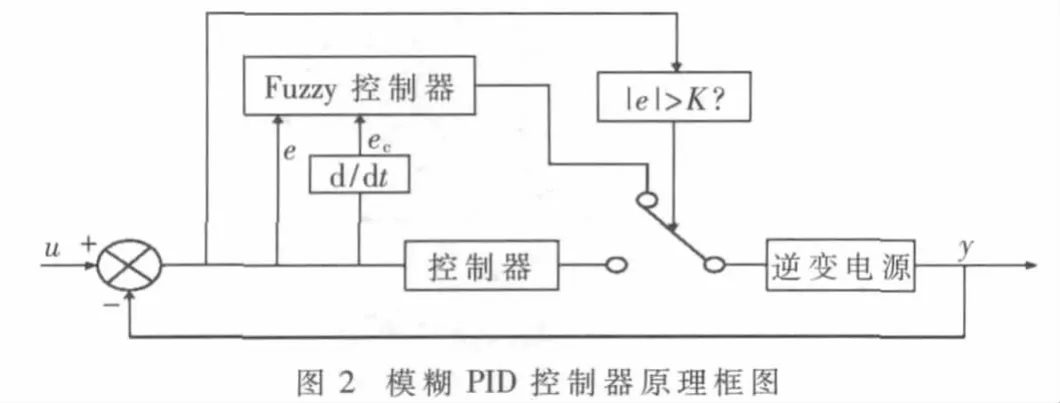
模糊控制器的实现首先应定义输入输出变量的模糊集，确定各变量论域，建立模糊变量赋值表，即模糊化；然后根据实践和学习积累的经验，归纳出若干条控制规则，根据控制规则进行模糊推理，采用最大隶属度法，对输出加以清晰化处理。

1.2.1 模糊化

单相逆变电源采用二维模糊控制，需要考虑的论域有三个：输出电压偏差、偏差变化率以及控制量，选取电压偏差、偏差变化率作为输入。其中：

式中，y为输出值，urin为给定值，T为采样周期。

首先应对这些论域进行模糊化，采用Mamdani提出的标准化设计方法，在电压误差控制中，将此三种论域离散为[-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6]13个等级，e和ec会在正、反两个方向变化，可将[-6，6]分为负大NB、负中NM、负小NS、零ZE、正小PS、正中PM、正大PB这7个语言变量值。

根据实际经验，把测量偏差e的基本论域[-Xe，Xe]、偏差变化率ec的基本论域[-Xc，Xc]以及控制量u的基本论域[-Xu，Xu]量化到区间[-6，6]，这样就可以得到量化因子Ke、Kc和比例因子Ku。

然后根据离散化公式，将基本论域量化到量化论域中，具体的做法是：当基本论域是[a，b]，量化论域是[-n，n]时，n取6，利用式(8)实现量化：

1.2.2 模糊控制的隶属函数和控制规则的确定

模糊控制规则应根据系统期望的动、静态特性来确定，即当偏差较大时，控制系统的主要任务是消除偏差。此时，偏差的权系数应较大；而当偏差较小时，为了减小超调，并使系统尽快稳定，主要应根据偏差变化率来改变控制量，此时，要求加大偏差变化率的权重。下面说明模糊控制规则表的制定。

（1）根据以往在控制过程中的实践经验加以总结，可得到数条模糊条件语句的集合。将偏差和偏差变化率的语言变量值各分为7个等级，可以总结出7×7=49条模糊条件语句，具体描述如下：

（2）根据以往的经验知识和反复的实验，采用三角形隶属函数形式，可以得到如图3所示的偏差e、偏差变化率ec以及控制量U的隶属度函数。据此确定对应论域中起作用的控制规则，并制定如表1所示的模糊控制状态表。

1.2.3 解模糊与模糊PID控制器的实现

在本设计中，利用CRI法则推理时控制过程是用查询控制规则表来产生控制量的，对误差信号e和误差变化率ec论域中全部元素的所有组合进行计算，便可计算出模糊控制量的输出U，并采用最大隶属度的规则进行模糊决策，将U经过清晰化转换成相应的确定量。通过查表得到的输出控制量，还需乘上比例因子Ku，即得到调制波。

图3 隶属函数

表1 e、ec、U的模糊控制规则表

设计该模糊PID控制器的特点是根据输入在最大偏差范围内，利用模糊推理的方法调整系统的控制量，而在最小偏差范围内转换成PID控制，两者的转换根据事先给定的偏差范围自动实现，以实现系统控制量的自动调整。

2 系统仿真结果分析

图4 系统仿真结果

根据以上分析在Matlab/Simulink7.1环境下，建立控制模型。其中，采样周期T取0.001；经验证误差基本论域取[-35，35]，误差变化率基本论域取[-5，5]，控制输出量基本论域取[-40，40]，经推理模糊化因子0.02，kU=6.5；PID的参数Kp=1.2、Ki=10、Kd=0.000 5；开关频率为3 kHz，输入交流电压为380 V；交流负载电压220 V/50 Hz，120 000 kVA，输出滤波电容、电感分别为3 mH、5 000 μF；输出变压器参数380 V/120 V，250 000 kVA。

在电路仿真过程中，分别用普通PID和模糊PID控制对静变电源实施控制，开关阈值选为5 V，3个电压表分别测量与之对应的单相输出电压，仿真时间为0.5 s，仿真结果如图4所示。

根据仿真结果，静变电源从启动到电压稳定时，模糊PID控制效果明显比PID控制效果要好，而且在0.2 s突加负载、0.3 s断开负载时的电压能很快地恢复稳定；PID控制在突加和断开负载时电压波动大，恢复稳定所需时间长。由此可见，模糊PID控制静变电源的策略，兼具了模糊控制的动态特性和PID控制的稳态性能，使系统的稳态性、超调量得到了较大改善，提高了系统的响应速度和控制精度。

本文将模糊推理算法引入PID控制器中，解决了PID控制器在非线性系统中的收敛速度慢和误差精度低的难题。通过仿真实验，模糊PID控制器在线控制静变电源，其鲁棒性和自适应能力较强，对于干扰也有较好的抑制调节能力，满足了对静变电源输出的要求。整个系统的仿真结果验证了模糊PID控制算法应用于静变电源的正确性和可行性。

[1]李士勇.模糊控制·神经网络控制和智能控制论[M].哈尔滨：哈尔滨工业大学出版社，1996.

[2]王兆安，黄俊.电力电子技术[M].北京：机械工业出版社，2000.

[3]张国良，曾静，柯熙政，等.模糊控制及其MATLAB应用[M].西安：西安交通大学出版社，2002.

[4]Yang Hongjun.Researching on an automatically leveling control system based on Fuzzy-PID[C].The eighth nations experiment with measure colloquium.2009：2619-2622.

[5]郝少杰，方康玲.基于模糊PID参数子整定的温度控制系统的研究[J].现代电子技术，2011(4)：196-204.