一种改进的自然纹理合成方法
李大锦
(山东师范大学传媒学院,山东 济南 250024)
基于样图的纹理合成的实质是根据给定的一张样本图像,通过分析其像素颜色的统计规律性,重新生成一张任意大小的图像,生成的图像在视觉上与原样本图像非常相似。目前纹理合成主要是利用马尔科夫随机场的理论。基于马尔科夫模型,国内外学者已经提出较多的纹理合成算法,这些方法基本可归结为两大类:基于像素点的纹理合成[1-3]和基于块的纹理合成[4-6]。随后在这些基本合成算法的基础上,人们又提出了一些改进的合成方法[7-9]。 文献[7-8]提出的可并行计算的纹理合成方法,可有效地提高合成速度。为了减少基于块的合成方法中纹理块间的不连续,熊昌镇等[9]在基于块的合成方法的基础上利用不规则纹理块来实现逐块合成。Zhang等[10]基于像素的合成方法,利用基于特征的变形和融合技术,实现了纹理图案方向的改变和两种纹理间的渐变。此外,人们还提出了针对某类具体应用的纹理合成算法。Miyata等[11]提出的用于合成“铺路”图案的纹理合成方法以及Ashikhmin[3]的自然纹理合成算法;文献[10,13]分别提出了两种多尺度纹理合成算法,在合成过程中,可以将样本的图像任意缩放,形成不同尺度的纹理图案。
Ashikhmin的自然纹理合成算法是所有基于像素点的纹理合成算法中较快的一种,不仅适合自然景物的合成,对于随机性较强的纹理同样适应。它采用L型邻域搜索匹配点,同时将匹配点的搜索限制在L型邻域产生的候选点之中,既提高了合成速度,同时使合成图片像素间保持了良好的连续性。最近,岳晓菊等[14]也提出了一种Ashikhmin的改进算法,将Ashikhmin算法中的像素点改为像素块,虽然可有效的提高合成速度,但是却没有解决块间的不连续问题。
在Ashikhmin的算法中,由L型邻域产生的候选点有时会超越样图边界,候选点的越界是造成结果图像明显产生块间不连续的主要原因。在Ashikhmin的文章里没有给出很好的解决方法,对于越过样图底部的候选点,只是简单的用一个随机选取的有效点来代替。对于越过水平边界的候选点Ashikhmin没有明确指出如何解决。本文对Ashikhmin的算法进行了改进,通过在样图内部寻找边界点的最佳匹配像素将越界候选点重新定位,有效地解决了Ashikhmin算法中纹理块间的不连续问题。
1 Ashikhmin的自然纹理合成算法
Ashikhmin算法的合成顺序是从输出图像的第1行开始,从左至右逐行合成每个像素。采用L型邻域来计算匹配点的颜色误差。从已合成的像素中选取和待合成像素相邻的若干像素形成一个L型的像素邻域,如图1所示。
合成过程中记录下每个已经合成的像素在样本图像中的位置。对于待合成像素的L型邻域中每个已合成的像素,根据其和待合成像素的位置偏移,在样本图像中可以找到一个相同位置偏移的像素点(图1样本图像中黑色点),该像素点就是待合成像素的一个候选点。L型邻域中每个像素都产生一个候选点,待合成像素最终确定的采样点是所有候选点中匹配最好的候选点。候选点的匹配计算采用颜色空间的欧氏距离作为匹配标准。颜色距离计算如式(1)。
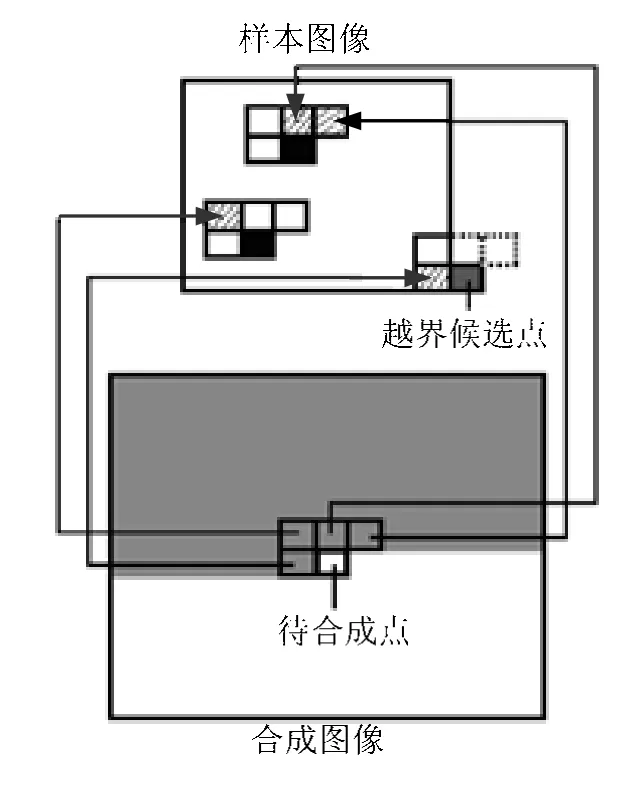
图1 Ashikhmin算法中候选点的确定

其中,N1和N2分别是用于计算颜色距离的样本图像和目标图像L型邻域。R、G、B分别是在p点处像素的红、绿、蓝颜色值,下标1、2分别代表样本图像和目标图像。
Ashikhmin的算法描述如下:
用随机产生的坐标位置采样样本图像的像素填充目标图像,同时记录每个像素的采样坐标;
for( 扫描线顺序扫描每个点)
{
找出目标图像中当前点L型邻域内的所有点;
for( L型邻域内的每个像素点 ){找到该像素的候选点,插入到候选点列表中;}
将候选点列表中相同的候选点删除;
for( 每个候选点 ){计算其L型邻域和当前待合成像素L型邻域的颜色误差;}
将颜色误差最小的候选点像素拷贝到当前合成像素,并记录其在样本中的坐标;
}
Ashikhmin算法的合成过程实质上是像素块的生长过程,像素块呈不规则状。纹理块从某个位置开始沿着垂直方向逐步向下生长,当纹理块生长到样本图像的底部时会产生无效的候选点。Ashikhmin给出的解决方案是:将样图中的像素与样图底部的距离坐标规格化为[0,1]之间,规定一个标准距离d∈[0,1],然后随机产生一个距离rand∈[0,1],满足rand4﹥d;在样图中取该点对应的候选点代替越界的无效候选点,由随机产生的有效候选点开始继续纹理块的生长。Ashikhmin没有给出如何解决水平越界候选点的问题。一般的方法是通过将候选点的水平坐标x对样图宽度取模运算,循环采样样本图像;或者同样采用Ashikhmin解决垂直方向越界的方法,随机产生有效候选点。
Ashikhmin算法合成的结果图像块在竖直方向上是不规则的,但在图像块生长到样本图像的底部时会产生明显的水平分解线。由于样本图像底部和随机产生的候选点像素没有任何相关性,在视觉上也不能形成平滑的过度,导致了明显的块间跃变。同时由于候选点的随机性还导致了上下两个纹理块之间的像素比较紊乱。
2 改进的自然纹理合成算法
针对上述Ashikhmin算法的不足,本文对原Ashikhmin算法进行了改进。将样本图像的底部和右侧边界区域用样图内部其他的像素块代替,使合成中的图像块在生长到接近边缘处时转向样图内部某个区域重新开始生长。
受文献[5]“图像缝合”思想的启发,将边缘处一定宽度的像素块用样图内的最佳匹配像素块来代替。取靠近样图边缘的1/4样图高度的区域(图2中2区域),在样图中寻找与之匹配的区域(图2中的1区域),匹配误差的计算采用式(1)的方法。匹配区域确定后,再确定两块区域的“缝合线”。这条缝合线将两块区域各划分出两部分(图2中的白色线),将区域2中处于缝合线以下的部分用区域1的缝合线以下的区域像素来代替。在合成过程中当纹理块生长到缝合线处时,会转向替代区域的位置,重新进行纹理块的生长。为了避免再生长的纹理块很快又到达底部,在寻找匹配区域的时候,将匹配区域限制在样本图像上部的1/2之内。因为处于缝合线两侧的两个像素块的相邻像素颜色距离差别最小,所以缝合后的图像在视觉上不会看到明显的分界线。

图2 边缘像素区域的替代
缝合线的计算确定采用最短路径法,首先要建立一个有向无环图(见图3所示)。以求水平缝合线为例,有向无环图的建立方法是:将两块图像重叠合,图3中圆圈是两个图像块重叠的像素。先在重叠图像的左右两侧建立两个节点,作为有向无环图的开始和结束节点;在图像中每四个相邻像素的中间也分别建立节点(图3中黑色方块);然后从左到右用弧连接这些节点,上下每相邻的两个节点也都用一条弧相连。取弧的左右两边重叠像素的颜色误差eij作为每条弧的权值。从开始点到结束点的一条最短路径即是最佳匹配的缝合线。权值eij的计算如下:

图3 用于计算缝合线的有向无环图

式中,eij是像素(i,j)到像素(i,j+1)之间的颜色误差;Eij是两个匹配区域对应点(i,j)处颜色的误差;C1、C2分别是两个匹配区域某点像素的颜色值,下标i,j指对应像素的坐标,上标r、g、b分别指3个颜色通道。
另外需要一个用于索引样本坐标的索引二维数组,存放样本中每个像素对应的实际坐标,用匹配的区域替代边缘区域以后,被替代边缘区域的像素坐标索引应指向替代区域的坐标。在合成过程中,从索引数组中查找像素的位置。在初始化输出图像时,我们不用单个像素,而是采用随机产生的像素块来初始化索引数组。像素块的大小根据纹理特征的不同来确定。实验证明:对于结构性较强的纹理,像素块取基本纹理元素的1~3倍。对于一般的自然纹理,可取样图大小的1/8~1/4。
改进后的算法描述如下:
用随机产生的像素块初始化坐标索引数组。
搜索匹配区域,建立有向图并计算最小路径,将替代区域的坐标填入索引数组中样本边缘被替代的区域。
用随机产生的坐标位置采样样本图像的像素填充目标图像,记录对应索引数组中的像素坐标
For(扫描线顺序扫描每个点)
{
找出目标图像中当前点L型邻域内的所有点;
For(L型邻域内的每个像素点){在索引数组中找到候选点并插入到候选点列表。}
将候选点列表中相同的候选点删除;
For(每个候选点){计算当前候选点L型邻域和当前待合成像素L型邻域的颜色误差;}将颜色误差最小的候选点像素拷贝到当前合成像素,并记录其在样本中的坐标;
}
3 结 果
图4中的白色线是合成后的图像中纹理块的边界,图4(a)是Ashikhmin方法合成结果,图4(b)是本文方法合成的结果。可以看出本文的算法在竖直和水平两个方向上都形成了不规则的像素块边界,避免了紊乱像素的产生,同时,从图4(b)可以看到本文的方法生成的像素块相对较大,能在更大范围内保持了像素的相关性。
图5给出了本文算法和原Ashikhmin算法的合成结果的比较。可以看出,本文算法的结果要明显优于Ashikhmin算法,尤其对于结构性较强的纹理,能很好的保持纹理的结构特征。
在算法时间效率上,本文算法比原来算法增加了寻找替代像素区域和“缝合线”的计算,但是在实际应用中这些计算可以作为预处理阶段事先处理,在合成过程中本文算法不再增加任何额外时间。

图4 合成后的纹理块边界

图5 原方法和本文方法的结果比较
4 总 结
本文基于自然纹理合成算法,提出了一种改进的自然纹理合成方法,解决了原算法中候选点的越界问题,有效地降低了纹理块间的明显变化。实验结果表明:使用本文的合成方法,合成效果得到了很大的改善。
[1]Efros A A, Leung T K. Texture synthesis by nonparametric sampling [C]//Proc of the International Conference on Computer Vision. Washington D C,USA: IEEE Computer Society, 1999: 1033-1038.
[2]Wei Liyi, Levoy M. Fast texture synthesis using tree-structured vector quantization [C]//Proc of the International Conference on Computer Graphics and Interactive Techniques. New York, USA: ACM Press,2000: 479-488.
[3]Ashikhmin M. Synthesizing natural textures [C]//Proc of ACM Symposium on Interactive 3D Graphics.New York, USA: ACM Press, 2001: 217-226.
[4]Liang L, Liu C, Xu Y Q, et al. Real-time texture synthesis by patch-based sampling [J]. ACM Transactions on Graphics, 2001, 20(3): 127- 150.
[5]Efros A A, Freeman W T. Image quilting for texture synthesis and transfer [C]//Proceedings of SIGGRAPH2001, New York: ACM Press, 2001:341-346.
[6]Kwatra V, Arno Sch¨odl ECT. Graphcut textures:image and video synthesis using graph cuts [C]//Proceeding of SIGGRAPH03. New York: ACM Press,2003: 277-286.
[7]陈 昕, 王文成. 大尺寸纹理的实时合成[J]. 软件学报, 2009, 20: 193-201.
[8]Lefebvre S, Hoppe H. Parallel controllable texture synthesis [J]. ACM Trans on Graphics, 2005, 24(3):777-786.
[9]熊昌镇, 黄 静, 齐 东. 基于不规则块的纹理合成方法[J]. 计算机研究与发展, 2007, (4): 701- 706.
[10]Zhang Jingdan, Zhou Kun, Velho L, et al. Synthesis of progressively-variant textures on arbitrary surfaces [J].ACM Transactions on Graphics, 2003, 22(3):295-302.
[11]Miyata K, Itoh T, Shimada K. A method of generating pavement textures using the square packing technique [J].The Visual Computer, 2001, 17(8): 475-490.
[12]Han C, Risser E, Ramamoorthi R, et al. MultIscale texture synthesis [J]. ACM Trans. on Graphics, 2008,27(3): 1-8.
[13]李大锦. 可控的连续多尺度纹理合成[J]. 计算机工程, 2009, 35(24): 211-212.
[14]岳晓菊, 康宝生, 闫丽君. 利用相关性原理纹理合成的改进算法[J]. 计算机工程与应用, 2011, 47(10):190-192.

