基于蒙特卡罗方法的矩形布局问题研究

郑荣杰， 张鹏程， 崔海良， 李国顺， 罗海兵， 刘昕彤

（河北工程技术高等专科学校，河北 沧州 061001）

矩形布局[1]是在矩形的边与布局空间边界平行的情况下，将其不相嵌地放入布局空间中，同时达到空间排布的最优化。这一问题属于布局问题的一个子问题。它在机械设计与制造、交通运输、大规模集成电路设计等领域有着广泛的应用，是当前CAD/CAM研究的热点问题之一[2]。

布局问题作为具有NP-hard的最优组合问题，在有限的时间内一般无法获得全局最优解[3]。对其求解只能依赖于各种启发算法，其中构造式启发方法应用最广[4]。使用构造式方法求解矩形布局，其过程分为定序和定位两步:定序规则确定矩形布入的次序，定位规则确定矩形布入位置。矩形可行域是指待布矩形在布局空间中所有可行位置的集合。近来，研究发现结合矩形可行域制定定序规则和定位规则，可以使矩形布局过程更灵活，算法的自适应性更强[4]。

随着矩形布入，布局空间的边界发生变化，边界的形状变得复杂。确定此类空间中矩形可行域成为一个难题。考虑到蒙特卡罗方法研究非确定性问题的优势[5]，我们将其引入到于矩形可行域研究，最终得到了有意义的结果。

1 蒙特卡罗方法

蒙特卡罗方法[6]，是一种根据统计抽样理论近似求解数学物理问题的计算机模拟方法，已广泛应用于金融工程学，宏观经济学，生物医学，计算物理学等领域。对于确定性问题，其基本思想是：建立一个与所求解有关的概率模型，基于这个模型进行随机抽样；通过对随机抽样进行统计，得到概率模型的分布或数学期望作为近似解。对于非确定性问题，蒙特卡罗方法则无需将非确定性问题转化为确定问题再求解，而是直接从非确定性问题出发，通过模拟问题的实际过程得到问题的解。考虑到布局问题具有非确定性,采用蒙特卡罗方法对矩形布局过程进行直接模拟，可以获得一种有效的布局方案。

2 矩形可行域

矩形可行域是指矩形在布局空间中所有可行位置的集合。在规则的布局空间中，矩形的可行域为矩形沿布局空间边界移动时，矩形的中心形成的封闭轨迹占据的区域。如图1所示，长为2，宽为1的矩形在边长为5的正方形中沿边界移动，得到多边形占据的区域即为矩形可行域。

图1 正方形布局空间中矩形的可行域

随着矩形布入，剩余布局空间的边界发生变化，成为不规则的布局空间。对于此类布局空间，可行域不能由矩形沿着空间边界移动直接得到。如图2所示，在布局空间左下角布入一个矩形后，下一个矩形在沿剩余布局空间边界移动时，位于位置1时满足边界条件；位置2时，则不符合。

如何得到不规则布局空间中符合边界条件的可行域是计算可行域的难点。王金敏等提出偏移多边形法，利用布局空间顶点的坐标及布局矩形的尺寸关系进行比较得到矩形可行域的边界[7]。此方法较好的解决了这一问题，但在计算可行域边界时，算法较为复杂。本文使用蒙特卡罗方法控制矩形在布局空间中移动，由边界条件限制矩形布局的范围，可行域的边界自动满足布局空间边界条件，简化了可行域边界的确定过程。

图2 剩余布局空间中矩形的可行域

3 矩形可行域求解算法及步骤

使用蒙特卡罗方法确定矩形可行域的步骤如下：

1）将布局空间划分成若干个格子。

2）确定矩形在布局空间的初始分布。依次在布局空间的顶点上设置满足边界约束条件的矩形，使得矩形可以到达布局空间的任何区域。

3）布局空间中，矩形按照蒙特卡罗法得到的随机步长沿水平或垂直方向做试探移动；同时矩形的移动需满足布局空间的边界条件。

4）统计满足布局空间边界条件的矩形中心分布位置。

5）根据矩形中心的分布位置得到矩形可行域。

下面给出了不规则布局空间中矩形可行域的求解实例。如图3所示，布局空间是一个不规则多边形，在x轴上位于区间[0,20]，y轴上位于区间[0,16]内。待布矩形是长为4，宽为2的矩形。为了保证矩形可以到达布局空间的任何位置，矩形在布局空间中初始位置需要满足条件：矩形至少有一条边和一个顶点分别与不规则多边形的边和顶点重合，并且位于布局空间内。如图2中所示，虚线构成的阴影矩形作为矩形的初始位置。

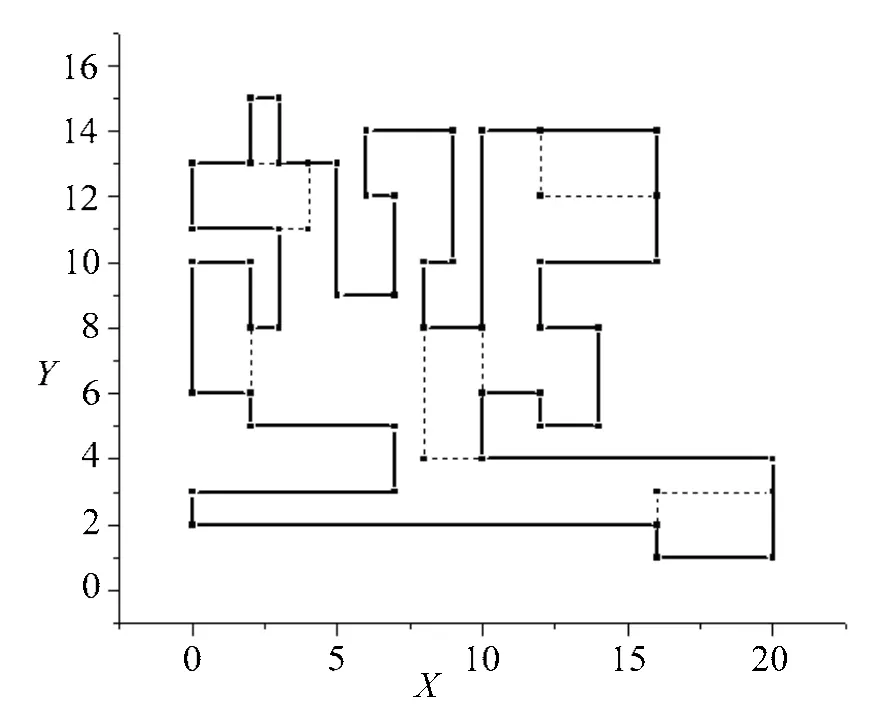
图3 不规则布局空间及矩形的一些初始分布位置

矩形按照蒙特卡罗方法产生的随机步长在布局空间中沿水平或垂直方向试探移动。如果矩形在试探移动后，仍位于布局空间内，则记录此时矩形中心的位置；否则不记录，做下一次试探移动。统计矩形的中心在布局空间中分布区域，即得到如图4所示的矩形可行域。图4中的点、直线以及闭合曲线占据的区域即为矩形可行域。其中，点表示此处只存在一种矩形的放置方式；直线表示矩形的中心可以沿着此直线运动。图中闭合曲线围住的区域表示矩形中心可在此区域内运动。

图4 矩形在布局空间中的可行域

显然，通过蒙特卡罗方法移动的矩形，自动满足布局空间的边界条件；得到的可行域边界必然同样符合布局空间边界约束。该方法在模型及算法上较传统方法更为直观，简单。

4 实例分析

利用蒙特卡罗方法确定矩形可行域，采用王金敏提出的定位函数及吸引子方法进行矩形的定位，从而完成矩形的布局过程[4]。定位函数的具体形式为

采用java语言完成了自动布局系统的设计。在Pentium(R) Dual-Core (2G/2.5GHz)微机上，测试了 http://people.brunel.ac.uk/～mastjjb/jeb/orlib/files/strip3.xls下载的实例数据，验证了本算法的有效性。在图5中，给出了strip3.xls文件的T1表中两例17个矩形在布局空间中的典型测试结果。图6为矩形占据布局空间的比例随着布入矩形数的变化规律。在实例1中矩形最终占据布局面积比例为91.653%，实例2中为91.368%。结果显示，使用蒙特卡罗方法得到的矩形可行域，应用于矩形布局时，可以达到较好的布局效果。

图5 实例中矩形的布局结果

图6 矩形占据布局空间比例与布入矩形数的关系

5 结 论

本文基于蒙特卡罗方法研究矩形布局问题。使用蒙特卡罗方法控制矩形在布局空间中移动，由边界条件限制矩形布局的范围，得到的可行域边界自动满足布局空间边界约束。结合定位函数,最终获得了良好的布局结果。该方法很大程度上简化了可行域边界的确定过程，最终提高了布局算法的效率。

使用蒙特卡罗方法确定矩形的可行域，计算过程只受布局空间边界约束，与待布矩形的形状和位置无关，所以在确定边界条件的前提下，该方法可扩展应用于矩形、三角形和圆形的混合布局问题。

[1]Dowsland K A, Dowsland W B. Packing problem [J].European Journal of Operational Research, 1992,56(1): 2-14.

[2]Sweeney P W, Paternoster E R. Cutting and packing problem: a categorized application-orientated research [J]. Journal of Operation Research Socity,1992, 43(7): 691-706.

[3]王金敏, 喻宏波, 陈东祥, 等. 布局模装系统的研究[J].工程图学学报, 2001, (1): 47-54.

[4]王金敏, 杨维嘉. 动态吸引子在布局求解中的应用[J].计算机辅助设计与图形学学报, 2005, 17(8):1725-1730.

[5]马海云, 齐小军. 蒙特卡罗仿真机及其应用[J]. 电脑与信息技术, 2006, 14(3): 8-10.

[6]Metropolis N, Rosenbluth A W, Rosenbluth M N, et al.Equation of state calculations by fast computing machines [J]. J. Chem. Phys, 1953, 21: 1087.

[7]王金敏, 张鹏程, 朱艳华. 矩形布局可行域的确定[J].计算机辅助设计与图形学学报, 2008, 20(2):246-252.