基于空间投影的管道施工图自动生成研究
罗年猛, 龚小寒, 朱 林
(华中科技大学国家企业信息化应用支撑软件工程技术研究中心,湖北 武汉 430074)
在现代工业生产中,如图1中左图所示的空间管道在输送气体、液体或带固体颗粒的流体过程中扮演着至关重要的角色[1]。复杂的空间弯管,从图纸设计到工艺编制、模具设计、乃至现场安装,都存在着一定的难度[2]。在空间管道的生产或安装过程中, 如果能给技术工人提供直观易懂的管道二维工程施工图纸,则可以协助其高效快速地完成工作。在锅炉本体管道布置设计中,空间弯管的计算是必不可少的工作环节。以往,空间弯管的手工计算工作量大,计算繁琐[3]。大量的管道施工图绘制成为该行业项目开发一个很大的效率瓶颈,特别是对于一些结构相对复杂的空间管道而言,绘制其二维施工图更是费时又费力,稍有不慎就容易出错,严重影响企业的生产进度和效益。如何根据管道的相关参数信息快速生成施工图成为当前迫切需要解决的技术问题。本文依据锅炉企业对锅炉空间管道工程图的实际需求,提出了由管道三维坐标集合以及相关几何参数自动生成空间管道工程图的算法,并在某锅炉厂投入了实际应用,获得了良好的实际效果。

图1 空间管的形状及其简化图
1 管施工图技术要求
本文算法适用于等径、统一圆弧弯曲半径的空间弯管。一根复杂的锅炉空间管道,如果忽略管路的直径,可以由多个直线段以及直线段之间的圆弧光滑首尾相连构成。在特殊情况下,直线管段会退化为一个点,直接变成两段圆弧相切连接。在实际的管道施工图的绘制中正是利用了这种简化技术。如图1右图所示为平面上的忽略管路直径的空间弯管简化图。
在工程施工图中,为了满足空间管道的加工需求,施工图所需要表达的是管道简化后的各直线段的长度、弯曲的半径和长度、以及弯曲各段之间的扭转角度。为确定管路绘制的输入条件以及施工图的绘制要求,引入如下定义:
定义1 尖点。管路简化后的两直线段延长线或反向延长线的交点,如图2所示。

图2 尖点定义
定义2 二面角。在空间上,由于两条相交的直线确定一个平面,则根据图2的尖点概念,可知不在同一直线上的3个尖点确定一个平面,如果存在连续的4个尖点A、B、C、D,则前3个点和后3个点会分别构成两个平面,两个面之间的夹角即为二面角。二面角表达了管路在加工中的扭转情况,同时通过在二面角上做投影可以分别表达组成二面角的两个平面上的直线的实际长度以及直线段之间的圆弧的实际形状。当将两个平面向垂直于两平面的交线的投影面投影时,两个平面分别积聚为线,从而可以真实表达二面角,如图3所示。

图3 二面角定义
基于以上定义,结合企业的工程施工需求,空间管路的施工图自动生成的输入定义如下:
1)构成空间管的所有尖点的个数n以及每一个点的坐标
2)输出图纸的范围,即图框的一系列几何参数。
一张自动生成的空间弯管施工图包含如下几个部分:
1)主、俯、左视图,必要的局部视图以及二面角视图。要求所有的视图联系起来,能够完整表达空间管道各段的真实长度、弯曲半径以及扭转角度等信息;
2)根据输入信息自动确定图形的折断画法;
3)图框、标题栏及相关信息的自动添加。
2 关键算法及算法体系结构
鉴于该系统的高度自动化,在生成空间弯管工程图时,需要系统根据已知的输入参数自动选择最佳主视图投影方向进行投影;根据管段长度以及图框尺寸大小自动判断是否需要将长管进行打断处理,如需要打断则进行智能打断;根据三视图显示的信息与空间弯管的结构复杂度自动判断是否需要局部视图以及二面角视图辅助表达弯管信息,如需要则自动生成;自动添加图框、标题栏信息。
总体的操作流程如图4所示。

图4 总体流程图
2.1 主视图投影方向的选择
主视图是零件图中最重要的图形,主视图选择的合理与否直接影响到整个表达方案的合理性,选择主视图应考虑以下几个原则[6]:
1)特征原则 充分反映零件的结构形状特征。
2)工作位置原则 反映零件在机器或部件中工作时的位置。
3)加工位置原则 零件在主要工序中加工时的位置。
锅炉空间管道由于存在空间弯曲,加工位置不确定,工作位置由于是空间状态,也不便确定。因此应让主视图最大程度表示零件的基本特征和最多的零件信息。并在满足要求的前提下,使视图的数量尽量少,尽量避免使用虚线表达零件的结构[5]。根据上述主视图选择原则及锅炉管道特性,本算法中主视图的选择原则为:
1)使平行直线管段数目最多的直线组平行于坐标轴,这样可在弯管完成旋转后判断未尽表达二面角时减少二面角视图数量。
2)在相邻两直线管段组成的平面中,使有最多平行直线组参与的平面的法向量平行于坐标轴,这样将在弯管完成旋转后在判断未尽表达局部弯管时,减少局部视图数量。
3)如上述选择均不理想,既不存在平行直线,也不存在平行平面,则默认取第一条直线平行于Z轴,第一个平面平行于XOY平面。
4)尽可能减少向视图的数目,避免直线的相互交错,使施工图简洁易看[6]。
主视图投影方向的选择操作流程图如图5所示。

图5 主视图投影方向判断流程图
在对空间弯管进行投影变换前,需要先进行如下步骤的操作,以确定最合适的主视图投影方向:
第1步 求平行直线数目最多的平行直线组的方向向量nx,并将nx旋转至与Z轴平行;
所有直线管段中与直线Line1=D1D2平行的直线段数目记为c1,即直线方向向量外积n1×n2,n2×n3,…,n1×nk-1结果为0的数目为c1;与直线Line2=D2D3平行的直线段数目记为c2,即n2×n3,…,n2×nk-1结果为0的数目为c2;依此类推,nk-2×nk-1结果为0的数目记为ck-2。
若cx=max(c1,c2,…,ck-2),可知与直线段Linex=DxD x+1平行的直线最多,该直线的方向向量nx即所求。若c1=0,c2=0,…,ck-2=0,即所有直线均不平行,则令nx=n1。
第2步 最多平行直线组参与形成的平行平面的法向量Nx':
设直线Line1Line2组成平面M1,法向量为N1;直线Line2Line3组成平面M2,法向量为N2;依此类推,直线Linek-2Linek-1组成平面Mk-2,法向量为Nk-2。
分别计算平面法向量与最多平行直线组的方向向量的内积N1·nx,N2·nx,…,Nk-2·nx的值,若Nx·nx=0,则直线LinexLinex+1组成平面Mx即为所求平面。若计算结果全不为零,取直线Line1Line2组成的平面M1为所求。
平面Mx包含的3个尖点分别记为Dx,Dx+1和Dx+2。 经过第1步、第2步变换后尖点记为Dx',Dx+1'Dx+2',则平面Mx法向量即所求法向量为

对空间管道进行三维图形变换[7]:
(1)平移变换:将尖点Dx平移至原点,设平移矩阵T1,该矩阵的计算较为简单,这里便不作赘述;
(2)旋转变换:将直线Linex旋转至与Z轴平行,设旋转矩阵为T2,该矩阵的计算方法详见参考文献;
(3)旋转变换:将法向量Nx'旋转至平行Y轴,设旋转矩阵T3,该矩阵的计算方法详见参考文献。
经过以上3步矩阵变换,即可将空间弯管位于三维空间内的目的位置,所得数据点为

2.2 智能打断
结构复杂的空间管道,在忽略管道直径的情况下均可简化为多个直线段与直线段之间的圆弧段首尾光滑相连的简单模型。
在锅炉空间管道模型中存在长度较长的直线管段,如果生成工程图时不做任何处理直接进行投影,可能导致管道施工图中直线段与圆弧段之间的显示比例失调,并使施工图的尺寸过大,从而需要选用超大型图纸来绘制二维施工图。如果图框选择不合理,甚至会出现三视图超出图框范围的现象,如图6所示。这样既不利于读图,也将造成图纸空间的浪费。如果在投影前将长度超过一定极限的直线管段从中间做打断处理然后再进行三视图投影,这样即可以节省大量的图纸空间,也能清楚表达管道施工所需的全部信息,不影响读图。

图6 直接投影的三视图
如图6、图7所示,比较空间管道直接投影和进行打断操作后的投影结果可知,直接投影有可能使三视图超出图框范围,因此智能打断是非常有必要的。

图7 进行打断操作后的投影视图
在进行智能打断之前,需要先了解以下3个长度的概念:
1)Linen的真实长度lr:Linen起点记为nD、终点记为Dn+1,则
2)Linen的投影长度ls:即为直线段投影的起点与终点之间的距离;
3)打断长度lb:即直线管段打断的极限长度,lb为判断直线管段是否需要打断的标准。
智能打断算法的重点在于打断判断和打断长度的确定。
打断判断分两步进行,整体判断和遍历判断。整体判断是指从整体布局判断空间弯管的三视图是否超出图纸范围,从而判断是否需要打断弯管。当整体判断结果为需要打断时,才需要进行遍历判断,即遍历判断每一根直线管段的打断情况。
1)整体判断
设直接投影三视图在X、Y方向所占的尺为Xv、Yv,实际在图框范围内管道三视图可占用的范围为Xr、Yr。则直接投影三视图所超出图框范围的最大尺寸

若lextra<0,则直接投影后三视图完全位于图框范围内,不需要整体打断;否则需要进行整体打断。
2)遍历判断
以弯管的第n段直线管段Linen为例分析。先计算如下参数:
(1)空间管道最长直线管段长度lmax、最短直线管段长度lmin;
(2)投影距离边框的长度lleft(若投影超出边框,则该参数为负值)。
(3)投影距离边框的合理最小距离minlen,即布局留余值,最大距离maxlen视实际情况而定;
(4)需要进行打断的直线管段的数目m;
比较Linen的真实长度lr、打断极限长度lb以及投影长度ls之间的关系:
① 若lr ② 若lr>lb,则Linen需要进行打断。其起点位置不变,终点进行偏移。偏移向量 ③ 若lr 打断长度lb的确定比较繁琐,需要多次做出调整。打断操作并非能够一次到位,打断后需再次进行整体判断。如果三视图仍然超出图框范围,则调整打断长度再次进行打断操作,循环此过程直至三视图全部位于图框范围内。该算法中调整打断长度操作分为中调阶段与微调阶段。首次打断长度取 中调打断长度取 微调打断长度取 需要注意的是,为了防止形成死循环,需要控制微调循环次数。一般情况循环次数指定为20次即可达到要求。 根据上述的算法原理,设计的算法流程如图8所示。 图8 打断判断算法流程图 2.3.1 局部视图 由于管道的空间复杂性,连接圆弧段在基础投影面中的投影存在3种情况:圆弧、直线或者椭圆弧。如果连接圆弧在三视图中没有反映其实际形状,则不能完全表达弯管几何信息并给读图造成困扰。因此,需要增加反映连接圆弧实形的局部视图使施工图完整表达管道的所有信息。 空间管道的结构由连续的直线段和圆弧段的图元组成,将管道图元组合成相邻的直线—圆弧—直线图元小组进行分析。如图9所示,ABCDE为一图元组,该图元组包含直线管道AB、连接圆弧BCD和直线管道DE。将圆弧BCD所在平面标记为平面m,平面m的法向量标记为vec,3个基础投影面的法向量分别为vecX、vecY、vecZ。 (1)如果连接圆弧BCD所在的平面平行于基础投影面,向量vec与基础投影面的法向量外积为零,即满足下式中的任何一个 则圆弧在某个基础投影面内投影成圆弧,即三视图中能反映该圆弧实形,该图元组不需要局部视图; (2)如果向量vec不满足式(9),但连接圆弧所在平面垂直于基础投影面,向量vec与基础投影面法向量的内积为零,即满足下式中的任何一个 则连接圆弧在基础投影面投影成直线,需要增加局部视图,先将该图元组进行适当的矩阵变换后,再投影到基础投影面。例如图8所示图元组ABCDE所在平面垂直于XY平面,即连接圆弧BCD在基础投影面XY平面内投影成直线。平面m与XY平面的交线为L,法向量vec与Z轴的夹角为α。图元组ABCDE的变换过程如图9所示。先将图元组平移至原点,再将其绕直线L旋转角度α,至图元组ABCDE所在平面平行于XY平面,此时再进行投影操作即可得到反映连接圆弧实形的投影图。 (3)如果向量vec既不满足式(9),也不满足式(10),则连接圆弧投影成椭圆,需要在二面角视图中进行处理。先得到包含该圆弧段的二面角视图,可知在二面角视图中该圆弧投影成直线。则在二面角视图基础上,算法同上述情况(2)。 图9 局部视图变换示意图 2.3.2 二面角视图生成 由于管道的空间复杂性,其二面角错综复杂,很多情况下在三视图中无法标出二面角的大小。因此需要增加反映二面角实际大小的二面角视图以表达管道扭转情况。 由第1节所述二面角定义可知,由3条直线管段确定1个二面角。二面角主要分析直线管段的相对空间位置,所以可将空间管道模型再次进行简化,连接圆弧半径退化为0,空间管道变为空间直线首尾相连的简单模型。 将图元组合成直线AB—直线BC—直线CD的图元组进行分析,3段直线的方向向量分别记为vec1、vec2、vec3 (1)如果图元组中间直线BC平行于坐标轴,即中间直线方向向量与坐标轴方向向量外积为零 则该图元组的二面角在三视图中反映实形,不需要生成二面角视图; (2)如果图元组ABCD不满足式(13),但满足3段直线共面 且3段直线所在平面平行或垂直于基础投影面,即满足式(15)中的任何一式:则不需要增加二面角视图 (3)除了上述两种情况,均需要生成二面角视图来反映图元组的二面角大小。 生成二面角视图的算法如下: 首先选取图元组三视图投影中,中间直线管段投影最长的投影面m,并获取该投影面的法向量vec;然后旋转整个图元组,至中间直线平行于vec向量,以确保图元组向投影面m投射时,中间直线段投影成点;旋转变换完成后,将图元组整体向投影面m投影,即可得到能反映该图元组二面角真实角度的二面角视图。 利用上述算法,将其应用到InteCAD系统中,为设计人员提供了一套自动生成空间弯管二维施工图的CAD系统,并且投入到武汉锅炉股份有限责任公司的锅炉空间管道设计工作中使用。武汉锅炉厂提供的一根实例锅炉空间管道的一系列的尖点空间坐标值及弯管弯曲半径等参数值如表1所示。 表1 空间管道输入参数 输入这些参数即可得到空间弯管的施工图,包括空间管道的三视图、局部视图以及二面角视图。 通过研究空间弯管二位工程图自动生成的一系列要求,提出了合理的算法及解决方案,应用到实际的CAD系统中,证明了算法的可靠性和有效性。 [1]于国清, 董 珊, 等. 锅炉房汽水系统CAD的研究与开发[J]. 热能与动力工程, 2000, 15(5): 522-525. [2]于国清. 三维管道系统CAD中二维视图自动生成技术探讨[J]. 计算机应用, 2001, 21(10): 33-35. [3]童维璜. 空间弯管设计的坐标表示及其弯曲参数的确定[J]. 川齿科技, 1991, (10): 32-35. [4]朱德铭. 弯管的造型及其投影图的计算机绘制[J].工程图学学报, 1992, 13(1): 31-36. [5]童迎武, 华立新, 等. 空间弯管的一种计算方法——矢量代数法[J]. 锅炉技术, 1991, (5): 17-22. [6]常 明, 胥北澜, 等. 画法几何及机械制图(第3版)[M]. 武汉: 华中科技大学出版社, 2005: 9-13. [7]常 明, 李 丹, 罗年猛, 等. 计算机图形学算法与应用(第2版)[M]. 武汉: 华中科技大学出版社, 2009:103-119.



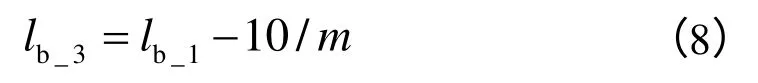

2.3 局部视图、二面角视图



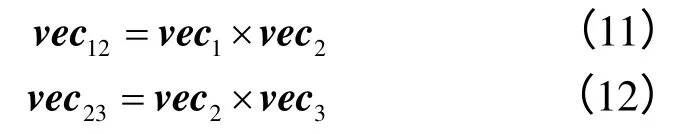



3 实例分析

4 结 束 语

