考虑自由段受荷的锚杆变形和承载特性研究＊

刘晓明，张亮亮

（湖南大学土木工程学院，湖南长沙 410082）

桩锚体系作为一种比较高效、经济的岩土支挡技术，广泛应用于深基坑工程中.采用预应力锚杆后的桩锚体系，其位移变形值［1－2］有显著降低.但在桩锚体系协同工作的计算中，锚杆刚度的合理取值是一个关键环节，因为锚杆较小的刚度变化，会带来桩身变形和配筋的较大改变，因此对锚杆的承载力和变形特性的准确把握显得尤为重要.

有关预应力锚杆的变形和承载性质，已有不少学者进行了研究［3－9］.文献［3－4］运用摩阻力的理想弹塑性模型分别得到临界锚固段长度及锚杆抗拔力的解析计算式；张季如［5］假定土锚间的剪切力与剪切位移呈线性关系，提出了荷载传递的双曲函数模型；还有不少学者［6－7］根据锚固体与岩石的界面性质，对岩石锚杆的荷载传递机理进行了深入的研究；文献［8－9］通过室内试验，提出了锚杆长度、直径及锚固段长度和拉拔力之间的关系，但这些研究基本都没有考虑自由段对锚杆承载性质的影响.近年来，随着桩锚体系应用的日益普遍，工程中发现总体上锚杆自由段灌浆饱满的桩锚体系，其桩身变形量比自由段灌浆质量差的要小，显示出锚杆自由段的施工质量也影响了桩锚体系的受力性能，于是工程中越来越重视自由段的灌浆质量，因此有必要开展自由段对锚杆承载力和变形特性的影响方面的研究工作.

本文根据锚杆全长受荷的特点，引入反映土层抗剪强度衰减的双折线模型，运用荷载传递理论，分析锚杆承载力和变形特性，在此基础上结合工程实例对比分析了考虑自由段受荷与不受荷2种不同情况下的P－s曲线关系的差异，得到一些有益认识，为桩锚体系的更深入的准确分析提供一些参考.

1 锚固体荷载传递模型的建立

1.1 锚杆变形分析及承载机理

桩锚体系中的预应力锚杆构造示意图如图1所示，在锚杆拉拔过程中，首先是锚杆自由段的钢筋发生弹性变形，自由段钢筋杆体将锚头受到的荷载P传递到锚固段的锚固体顶端，然后分配给自由段和锚固段，如图2所示.分配给锚固段的荷载记作P1，分配给自由段的荷载记作P2，且根据荷载关系有P＝P1＋P2.

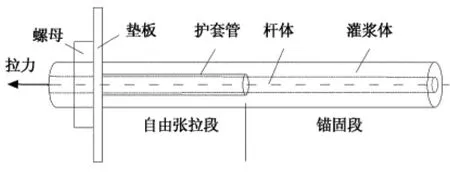
图1 预应力锚杆构造示意图Fig.1 The structure schematic drawing of prestressed anchor bolt

研究锚杆侧摩阻力传递机理时，为便于理论推导，作如下假定：

1）自由段荷载传递时仅考虑砂浆与锚固土层之间的摩阻力，忽略砂浆与护套管之间的摩阻力；

图2 预应力锚杆荷载分配图Fig.2 The load distribution map of prestressed anchor bolt

式中：P为锚杆拉拔力；lf为自由段长度，Es和As分别为杆体的弹性模量和截面积；sa为锚固段位移，sa＝sae＋sas.

随着基坑的继续开挖，土体的压力继续增大导致锚杆的拉拔力增大，锚杆的变形增大，拉拔力向更深部的土层传递，当锚固体与砂浆之间的粘结力抵抗不了土压力时，其剪切变形急剧增大且不收敛，锚杆即被整体拉出而破坏［10］.

1.2 锚杆侧摩阻力表达式

文献［11］根据土层锚杆的抗拔机理引入了砂浆与土层剪切强度的佐藤悟双折线模型，采用荷载传递法计算其摩阻力.该模型假定当土锚相对剪切位移未达到极限值时，摩阻力与剪切位移呈线性关系；但当土锚相对剪切位移达到极限值后，摩阻力不再发生变化，为某一定值，其模型界面本构模型图［12］，见图3曲线OAB.为了充分体现锚固体与土层之间

2）自由段和锚固段的土锚极限剪切位移和残余剪切强度相等；

3）锚固土层先于锚固体破坏，破坏面为锚杆与土层的交界面.

锚杆端部的总位移s是由自由段杆体的弹性位移sfe、锚固段杆体的弹性位移sae、锚固体与锚固层界面的剪切位移sas、自由段和锚固段杆体的塑性变形、杆体的调值以及锚具和垫板间的接触间隙等组成的［5］.一般杆体的塑性变形很小，可以忽略不计，通过对锚杆的预张拉可基本消除间隙的影响，因此锚杆的总位移可由式（1）确定：的抗剪强度衰减的特性，本文采用曲线OACD进行模拟，其摩阻力表达式为：

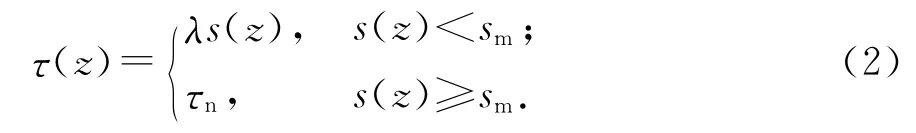
式中：λ为侧摩阻力传递系数，与锚固土层的性质、锚杆施工工艺和锚土界面处的粗糙程度有关；s（z）为锚杆z断面处的土锚相对剪切位移；sm为极限剪切位移；τn为砂浆与土层间的残余抗剪强度.其中λ值可以通过实测P－s数据线性拟合后进行反算求出.

图3 土锚界面本构模型Fig.3 Constitutive model at interface of soil and anchor

2 预应力锚杆位移方程的求解

2.1 基本微分方程的建立

根据荷载传递理论，锚固体内任一截面的控制微分方程为：

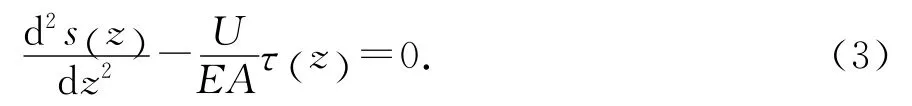
式中：U为锚杆的周长；E和A分别为锚固体的等效弹性模量和截面积.对于自由段，钢筋只承受拉应力作用，不参与荷载传递，锚固体为砂浆，其等效弹性模量为E＝Ea＝（EgAg）／A；对于锚固段，其锚固体为锚拉钢筋与砂浆的结合体，其等效弹性模量为E＝Ep＝（EgAg＋EbAb）／A，其中Eg和Ag分别为浆体的弹性模量和截面积.

2.2 微分方程的求解

根据锚杆的实际工作状态，锚杆在拉拔荷载作用下，锚固段OA段和自由段OB段分别出现塑性区，如图4和图5所示.坐标原点为自由段与锚固段相交界面处，对应的位移为sa，锚固段和自由段锚固体所取的微元如图4和图5中阴影部分所示，作用在锚头的荷载为P，传至锚固段顶端O点，锚杆锚固段和自由段的长度分别为la和lf，其对应的有效锚固长度分别为l1和l2.

图4 锚固段荷载传递分析简图Fig.4 Analysis of load transfer of anchor segments

图5 自由段荷载传递分析简图Fig.5 Analysis of load transfer of free segments

如图4所示，锚固段OA段为破坏区［s（z）≥sm］，破坏区深度为lp1，AC段为弹性区［s（z）≤sm］，其深度范围为lp1～l1，CE段未受荷载；同理，对于自由段，如图5所示，OB段为破坏区［s（z）≥sm］，破坏区深度为lp2，BD段为弹性区［s（z）≤sm］，其深度范围为lp2～l2，DF段未受荷载.对锚固段和自由段分别求解如下.

2.2.1 锚固段解答

对于锚固段，荷载传递如图4所示，在破坏区［s（z）≥sm］，将式（2）代入式（3）解得：

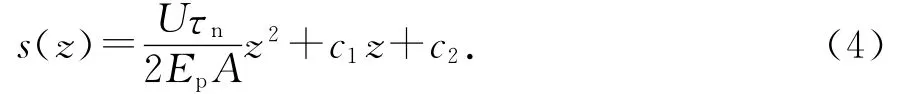
由O点（z＝0）的受力与变形条件，可得：

解得：

在破坏区与弹性区的边界A（lp1）点处，其位移刚好达到极限值sm，有：

根据式（7）可解出lp1：

在弹性区［s（z）≤sm］，将式（2）代入式（3），令α，解得：

由边界轴力条件：

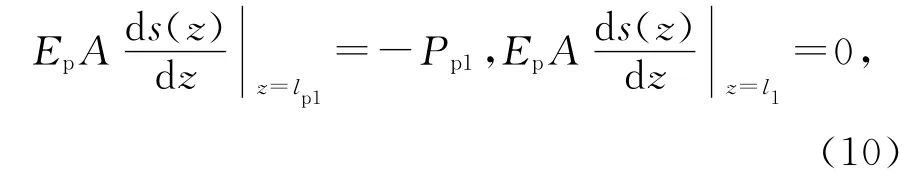
解得：

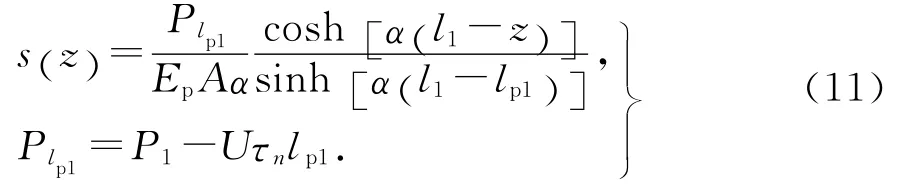
在A（lp1）点将位移连续条件s（lp1）＝sm代入式（11）解得：

将式（12）变形，求得l1为：

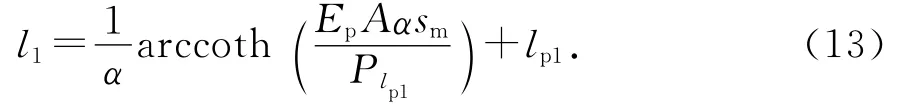
2.2.2 自由段解答

对于自由段，荷载传递如图5所示，其计算过程参照锚固段解法.在破坏区［s（z）≥sm］，有：

在弹性区与破坏区的边界B（lp2）处，将位移连续条件s（lp2）＝sm代入式（14）有：

由式（15）可以解得lp2：

在弹性区［s（z）≤sm］，解法同前，有：

在破坏区与弹性区的边界B（lp2）点处，将位移连续条件s（lp2）＝sm代入式（17），得：

由式（18）可以解出l2：

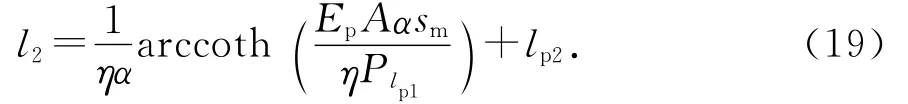
2.3 锚杆承载力与刚度表达式

1）锚固土层处于弹塑性阶段

根据荷载关系有：

为便于理解，可将式（12）和（18）分别变形为：

由式（7）和（15）可得：

由（1）（7）（20）可求得锚杆的总位移：

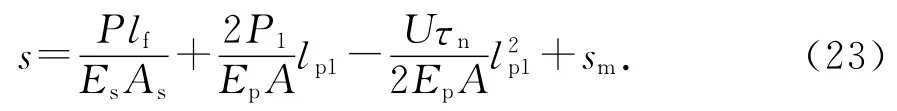
联立式（20）～（23）便可求得预应力锚杆在弹塑性阶段的荷载与位移之间的关系，此时锚杆锚固体破坏区产生了拉伸变形，弹性区的变形以剪切变形为主.当不考虑自由段承受荷载时，将上面相关式中的P1改成P，即可得到其荷载与位移之间的关系.

2）锚固土层处于弹性阶段

令lp1＝lp2＝0，式（21）可变形为

由式（20）可得：

由式（1）和（25）可求得弹性阶段锚杆刚度表达式：

12段作用时，ω＝tanh（αl1）.

3）锚固土层处于塑性破坏阶段，当锚杆整体全部发生破坏时，令lp1＝l1，lp2＝l2，将式（21）和（23）变形得：

不考虑自由段承受荷载时，式（27）中令l2＝0，式（28）中P1换为P即可得到相应的荷载位移关系.

3 实例计算与验证

为验证本文推导的理论公式的正确性，实例选取文献［5］中的锚杆现场抗拔试验中的锚杆M3，锚固层黏土呈硬塑状态，试验前对锚杆采用了0.1 Asfptk（fptk为锚拉钢筋的抗拉强度标准值）的拉力预张拉2次，对杆体进行调直，以消除锚具与垫板之间的接触间隙，锚杆进行过2次高压灌浆.有关参数如下：锚杆自由段长度为5.5m，锚固段长度为17.5 m，锚杆直径D＝130mm，截面积为A＝132.7cm2，锚拉钢筋为3φ25，弹性模量为Es＝2.0×105MPa，截面积为As＝14.7cm2，浆体弹性模量Eg＝2.0×104MPa，面积Ag＝118.0cm2，土体的残余强度为4 kPa.通过等效计算，可求得自由段锚固体等效模量Ea＝1.8×104MPa，锚固段锚固体的等效模量Ep＝4.0×104MPa.通过实测P－s曲线线性拟合，得P／s＝30.80kN／mm.由公式（26）可反算求得λ＝13.9 MPa，锚杆极限剪切位移sm＝4.6mm，采用本文计算模型，得到考虑自由段受荷与不受荷时锚杆的P－s曲线图（见图6）.

图6 锚杆P－s曲线计算值与实测值比较Fig.6 Comparison of calculated and measured P－s curves

图6中，实测P－s曲线与理论计算结果吻合较好，显示公式理论推导的正确性.从图中可以发现，与不考虑自由段受荷相比，考虑自由段灌浆受荷后不但极限承载力结果有较大提高，其曲线斜率明显比自由段不受荷的要大，显示锚杆刚度Km（图6所示初始直线段的斜率）也有一定提高.其中：承载力提高幅度近23%，刚度提高幅度近18.8%.

受计算参数取值影响，计算结果可能有些误差，但是有一点可以确认，考虑与不考虑自由段受荷的锚杆承载力和变形计算结果是有较大差异的，因此工程中应考虑锚杆自由段的影响.

4 讨 论

以上各公式推导表明：自由段长度、锚固段长度以及锚固体的材料性质等因素对预应力锚杆的抗拔承载性质有重要影响，本文将结合工程算例主要研究自由段对预应力锚杆变形和承载性质的影响.

图7所示为一组不同自由段长度所对应的P-s曲线图.从图中可以看出，同等条件下，自由段长度越长，相同荷载下锚杆产生的位移越大，曲线的斜率越小，即锚杆的整体刚度越小，其极限承载力也有所增加，增加幅度不是很大.因此在进行预应力锚杆的设计与计算时合理地选择自由段的长度显得比较重要.

图7 不同自由段长度的P－s曲线Fig.7 P－s curves for different free length

图8所示为锚杆刚度与自由段长度之间关系图.从图中可以明显地看出，锚杆刚度随着自由段长度的增加呈现减小的趋势，这与图7得出的结论一致.自由段长度增加到一定值后，曲线趋于平缓，此时自由段对刚度的影响不大.

图8 自由段长度对锚杆刚度的影响Fig.8 The influence of stiffness for different free length

从图6可以看出自由段受荷可以提高锚杆刚度.图9给出了锚杆刚度差异比与自由段长度之间的关系，锚杆刚度差异比是考虑自由段受荷与不受荷的刚度差值与考虑自由段受荷时锚杆刚度的比值，其可以较好地反映自由段受荷对锚杆整体刚度的影响情况.图中可以发现在lf＝5m时刚度差异最明显，自由段作用发挥很明显.

图9 自由段长度对锚杆刚度差异的影响Fig.9 The stiffness differences for different free length

5 结 论

针对预应力锚杆拉拔荷载由自由段锚固体和锚固段锚固体共同承担的特点，采用反映土锚界面强度衰减的双折线模型，基于荷载传递理论，研究了考虑自由段受荷的预应力锚杆变形及承载特性，并对比分析了自由段受荷与不受荷2种情况下的预应力锚杆P－s曲线图，得出以下结论：

1）自由段灌浆受荷的预应力锚杆，自由段和锚固段各自分担一部分荷载，并通过锚固体与锚固土层间的摩阻力作用将荷载传递到锚固体周围的岩土体中去.

2）自由段灌浆受荷后的预应力锚杆的整体刚度与极限承载力较自由段不受荷的都有明显的提高，自由段长度影响锚杆的刚度，在设计锚杆时应在合理的范围内取值.

3）工程算例表明本文计算方法与实测结果吻合较好，初步验证了计算模型的正确性，本文假定与实际情况会有些出入，因此对于基本假定的修正有待研究.

［1］ 张乐文，汪稔.岩土锚固理论研究之现状［J］.岩土力学，2002，23（5）：627－631.ZHANG Le－wen，WANG Ren.Research on status of anchor－age theory of rock and soil［J］.Rock and Soil Mechanics，2002，23（5）：627－631.（In Chinese）

［2］ 程良奎，范景伦，韩军，等.岩土锚固［M］.北京：中国建筑工业出版社，2002：75－88.CHENG Liang－kui，FAN Jing－lun，HAN Jun，et al.Rock soil anchoring［M］.Beijing：China Architecture ＆Building Press，2002：75—88.（In Chinese）

［3］ 张洁，尚岳全，叶彬.锚杆临界锚固长度解析计算［J］.岩石力学与工程学报，2005，24（7）：1134－1138.ZHANG Jie，SHANG Yue－quan，YE Bin.Analytical calculations of critical anchorage length of bolt［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（7）：1134－1138.（In Chinese）

［4］ 巍新江，危伟，张世民.理想弹塑性锚杆拉拔理论分析［J］.力学与实践，2006，28（3）：56－59.WEI Xin－jiang，WEI Wei，ZHANG Shi－min.Theoretical analysis of bolt pull out based on perfect elastic－plastic model［J］.Mechanics and Engineering，2006，28（3）：56－59.（In Chinese）

［5］ 张季如，唐保付.锚杆荷载传递机理分析的双曲函数模型［J］.岩土工程学报，2002，24（2）：188－192.ZHANG Ji－ru，TANG Bao－fu.Hyperbolic function model to analyze load transfer mechanism on bolts［J］.Chinese Journal of Geotechnical Engineering，2002，24（2）：188－192.（In Chinese）

［6］ 何思明，李新坡.预应力锚杆作用机制研究［J］.岩石力学与工程学报，2006，25（9）：1876－1880.HE Si－ming，LI Xin－po.Study on mechanism of prestressed anchor bolt［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（9）：1876—1880.（In Chinese）

［7］ 赵明华，龙照，邹新军.基于剪胀效应的桩底嵌岩锚杆荷载传递分析法［J］.岩土力学，2008，29（7）：1938－1942.ZHAO Ming－hua，LONG Zhao，ZOU Xin－jun.Load transfer method of rock－socketed anchoring rodsunder pile tip considering dilatancy effect［J］.Rock and Soil Mechanics，2008，29（7）：1938－1942.（In Chinese）

［8］ BENMORKANE B，CHENNOUF A，MITRI H S.Laboratory evaluation of cement－based grouts and grouted rock anchors［J］.Journal of Rock Mech Min Sci ＆Geomech，1995，32（7）：633－642.

［9］ COLLIN J G.Controlling sacrificial problems on reinforced steepened slopes［J］.Geotextiles and Geomembranes，1996，14：125－140.

［10］唐孟华.土层预应力锚杆应力损失及对策研究［J］.广州建筑，2008，36（3）：3—5.TANG Meng－hua.Research and countermeasure on the prestress loss of pre－stressed anchor in soils［J］.Guangzhou Architecture，2008，36（3）：3—5.（In Chinese）

［11］彭世明，赵明华.基于佐藤悟双折线模型的灌浆锚杆抗拔承载特性分析［J］.湘潭大学自然科学学报，2009，31（1）：104—109.PENG Shi－ming，ZHAO Ming－hua.Analysis of bearing characteristics anti－pull for grouted bolt based on Kezdi’s double－broken－line model［J］.Natural Science Journal of Xiangtan University，2009，31（1）：104－109.（In Chinese）

［12］孔宪宾，佘跃心，李炜，等.土锚杆相互作用机理的研究［J］.工程力学，2000，17（3）：80－86.KONG Xian－bin，SHE Yue－xin，LI Wei，et al.The mechanism study of soil－anchor interaction［J］.Engineering Mechanics，2000，17（3）：80－86.（In Chinese）