考虑边界条件的频率法测索力实用公式＊

唐盛华，方 志，杨 索

（湖南大学土木工程学院，湖南长沙 410082）

索结构广泛应用于斜拉桥、悬索桥以及中下承式拱桥等大跨结构中，索力直接控制结构的内力分布和几何线型，无论是在结构施工过程还是正常使用阶段，都需要能够及时准确地对索力进行测试.目前，索力的测试方法主要有液压表法、压力传感器法、测索伸长量法、磁通量法及频率法.现阶段以频率法最为经济、实用，因而应用最为普遍.

由拉索频率计算索力的方法主要可以分为有限元方法和公式计算方法，其中有限元方法［1－3］可以较好地模拟斜拉索的线型、边界条件、中间支撑等，并且可以同时使用多阶频率对拉索进行多参数识别，能够较好地识别包括索力在内的拉索参数，但是，此类方法一般需要编程或借助现有软件通过计算机实现，不便于工程应用.

公式计算方法要求建立索力与自振频率的显式关系，主要有2种方法，第1种方法由拉索的振动微分方程入手，建立频率特征方程，再根据边界条件对该方程进行求解，当拉索边界条件取两端固结时，得到的频率方程为超越方程，难以得到索力与频率的显式关系，为此，较多学者对其进行了研究.Robert等［4］提出了固结边界时拉索频率与弦理论频率的关系式.Zui等［5］以考虑弯曲刚度的拉索方程的高精度近似解为基础得到一组计算索力的实用计算公式.方志等［6］基于两端固结梁在轴向拉力作用下横向振动方程，拟合出轴向拉力与梁的抗弯刚度、长度、线密度及振动频率之间的数值关系.Ceballos等［7］基于振动微分方程，推导了可以考虑拉索抗弯刚度和端部转动约束刚度的索力迭代计算公式.张清华等［8］基于拉索自振频率的解析表达式，引入奇异摄动解法建立了由关键参数表示的拉索自由振动解析表达式.另一种方法必须先获得拉索的振型函数，再利用能量原理建立索力与频率的关系式.宋一凡等［9］引入压杆屈曲函数构造两端固结刚性拉索的1阶和2阶振型函数，再由RITZ法求得相应的1阶和2阶固有振动频率.任伟新等［10］采用能量法和曲线拟合方法，建立了分别考虑索垂度和抗弯刚度影响由基频计算索力的实用公式.甘泉等［11］将固支欧拉梁的振型函数作为两端固结拉索的振型函数，运用能量原理，推导了该类拉索的索力实用计算公式.这些表达式，多数以分段形式给出，在分段处不具连续性，有些在求解索力时需要进行迭代，有些仅适用于基频情况，使用起来不是十分方便.

本文通过两端固结梁和两端铰接梁的频率特征方程，在找出二者的频率关系后，建立了一个形式简单、物理意义明确而又具有良好计算精度和适用范围的索力计算公式.在此基础上，进一步分析了边界条件对索力计算的影响，建立了能够考虑拉索端部转动约束刚度的索力计算公式，本文公式简单适用，且具有良好的精度.

1 固结边界的索力计算公式

轴向拉力T作用下两端简支、两端固结梁横向振动的频率特征方程分别为［6］：

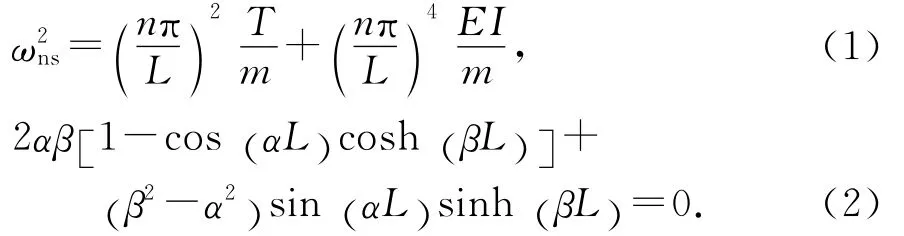
且

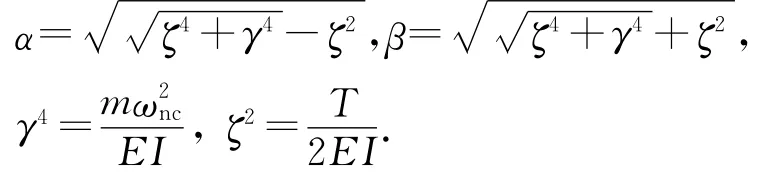
式中：m，L，EI和T分别为拉索的线密度、弦长、抗弯刚度及所受的轴向拉力；ωns，ωnc分别为两端简支和两端固结时拉索的振动圆频率；n为模态阶数.

假定ωns与ωnc满足如下关系：

对于一根具体的拉索，当m，L，EI和T都已知时，联立式（1）～式（3）可求得频率比值zn.

部分有代表性吊杆和拉索的参数分别如表1和表2所示（E＝2×105MPa）.反映拉索相对抗弯刚度的无量纲参数ξ如式（4）所示［10］，ξ值越小，拉索的相对刚度越大.

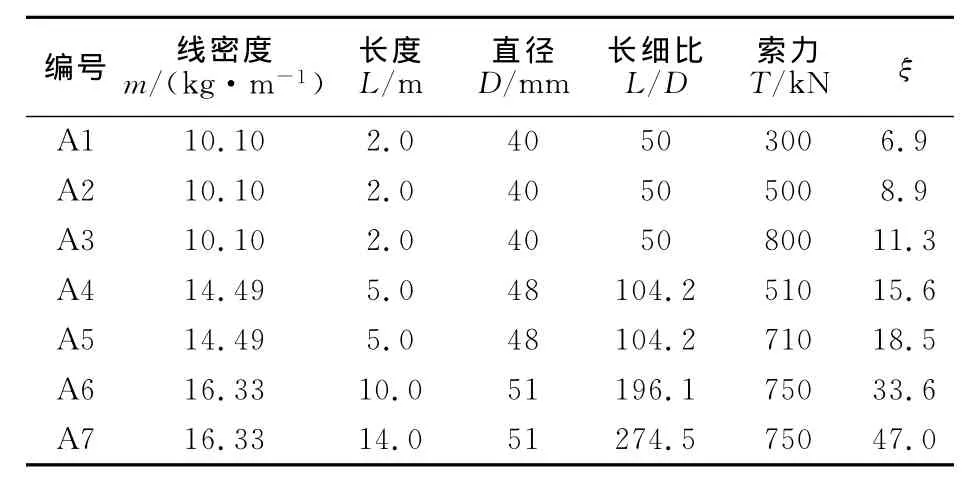
表1 吊杆参数Tab.1 Parameters of suspenders

表1中的A2，A4，A6吊杆的理论频率比值zn如图1所示，由图可知，吊杆ξ值越小，其频率比值zn越大，且频率比值随阶次的增加而减小.表2中的B1，B2，B4拉索的理论频率比值zn如图2所示，由图可知，对同一根拉索而言，其各阶频率比值基本相同，B1，B2，B4拉索的zn值依次减小.

记无量纲参数yn见式（5），对不同ξ值的拉索由式（3）可计算得到各阶频率比值zn，前6阶频率yn与zn的关系如图3所示.通过多项式进行拟合，比较了1～4次多项式的各种可能组合，考虑到计算精度和便于应用，选取1，3次项组合进行拟合，前6阶频率比值zn的拟合公式见式（6），图3中的实线为拟合公式的计算结果，和理论计算值吻合很好.

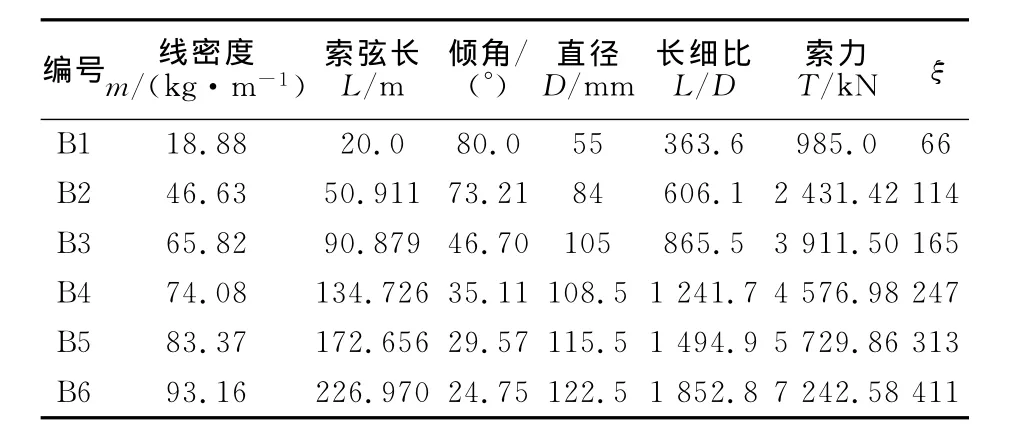
表2 拉索参数Tab.2 Parameters of cables

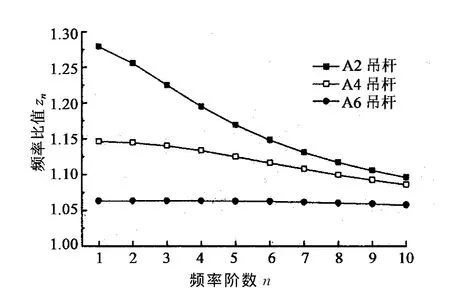
图1 吊杆频率比值znFig.1 Suspender frequency ratio zn

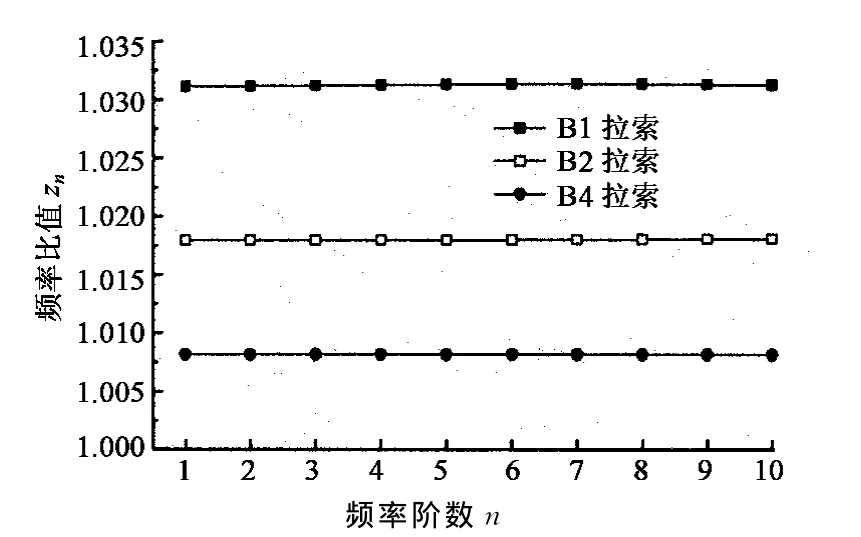
图2 拉索频率比值znFig.2 Cable frequency ratio zn

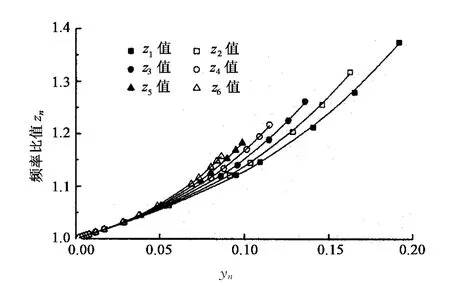
图3 拉索yn－zn关系曲线Fig.3 The relationship curves of yn－zn

进一步拟合得到频率比值zn的统一计算公式见式（7），于是可得索力计算公式（8）.可见，该索力计算公式形式较简单、物理意义明确.

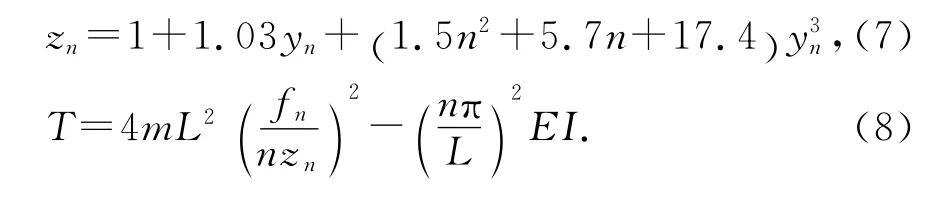
2 固结边界的索力计算结果比较

为验证本文索力计算公式的精度与适用范围，选取了部分有代表性吊杆和拉索进行分析，其参数分别如表1和表2所示.

基频吊杆索力计算误差的比较如图4所示.由图可知，公式（8）计算的索力整体表现最好，各吊杆的索力误差均小于1%，文献［5］和文献［10］的索力误差基本相同，不超过2.5%，文献［6］的公式整体表现稍差，最大索力误差也不超过2.5%.

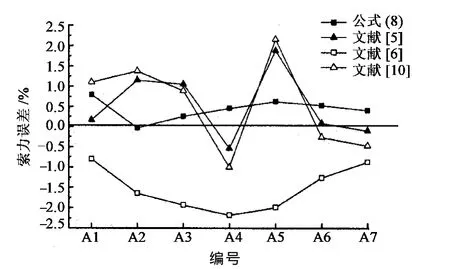
图4 基频吊杆索力计算误差Fig.4 First－order frequency cable tension calculation error of suspenders

公式（8），文献［6］和文献［11］计算的吊杆前5阶频率的索力误差分别如图5～图7所示.由图可知，公式（8）计算的各吊杆的索力误差均不超过2.5%；文献［6］计算的A1，A2吊杆的索力误差较大；文献［11］不同阶频率计算得到的索力离散性较大，索力误差最大，因而，公式（8）的适用范围更广.

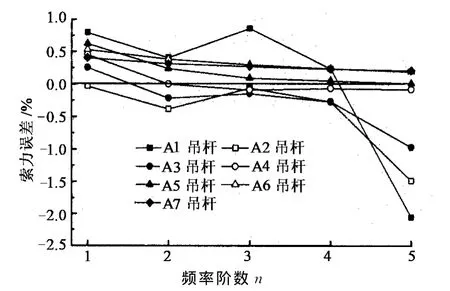
图5 公式（8）索力计算误差Fig.5 Cable tension calculation error of equation（8）

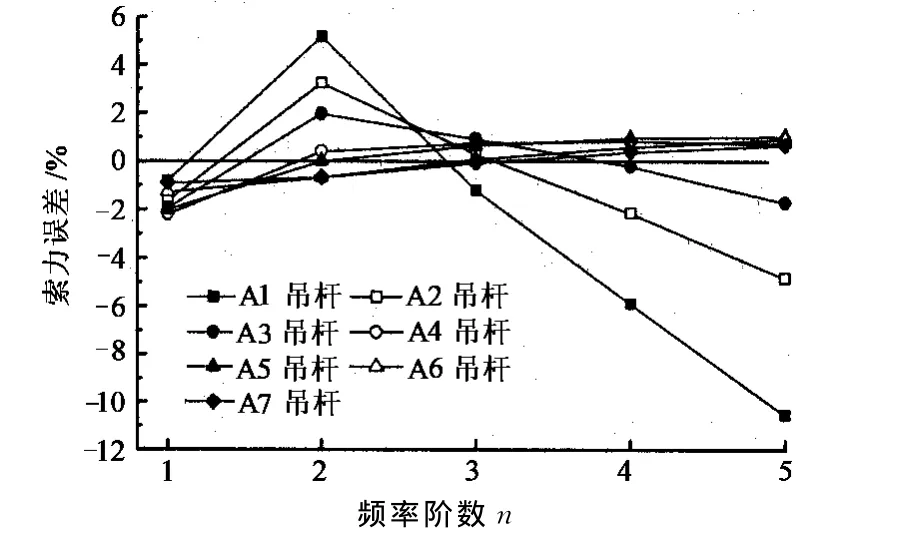
图6 文献［6］索力计算误差Fig.6 Cable tension calculation error of reference［6］

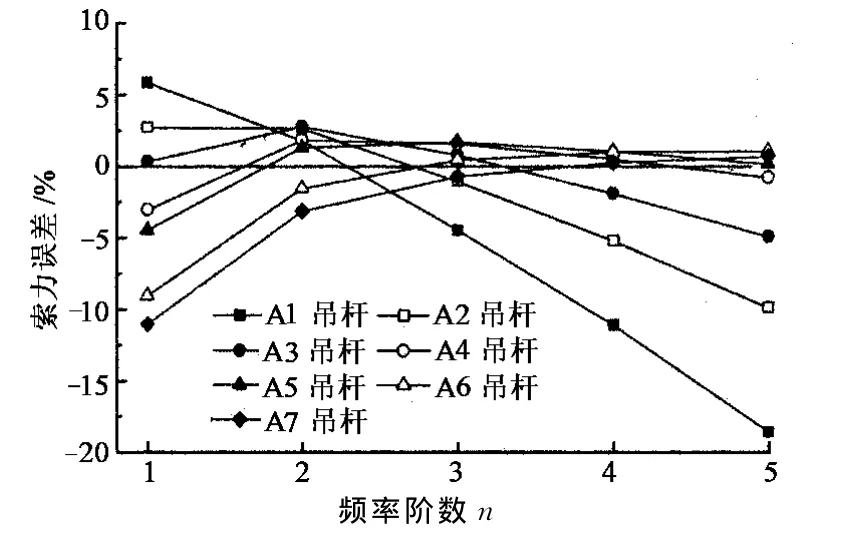
图7 文献［11］索力计算误差Fig.7 Cable tension calculation error of reference［11］

文献［4］给出固结边界时拉索频率与弦理论频率的关系式见式（9），可推出索力计算公式如式（11）所示，该公式适用于ξ≥50的拉索，世界上超过95%的斜拉索满足这一条件［12］，因而，对于斜拉索而言，该公式有较好的适用性.

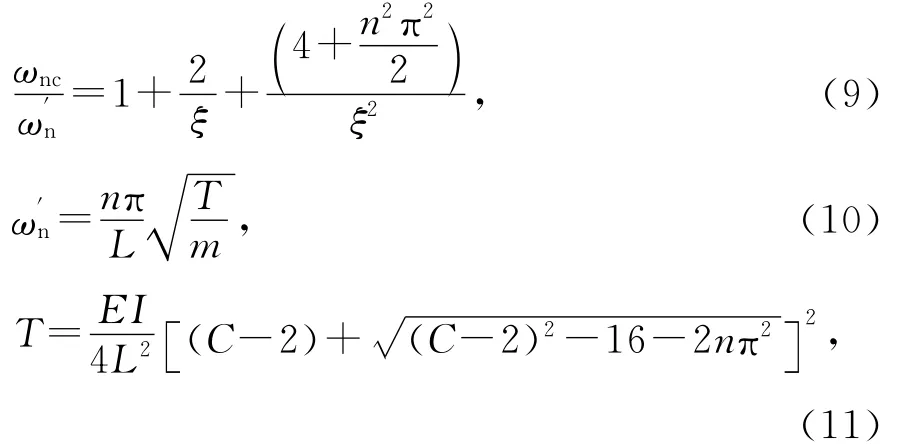
拉索前12阶频率计算的索力误差如图8～图11所示.由图可知，当拉索较长时，由于垂度的影响，公式（8），文献［4］和文献［6］由基频计算的索力均偏大（图9，图11），除1阶频率外，其他各阶频率由公式（8）计算的索力差别很小，误差均小于0.4%.当ξ≥115时，公式（8）和文献［4］的索力计算结果很接近，文献［6］由各阶频率计算得到的索力误差比公式（8）稍大，而文献［11］的索力计算方法需采用较高阶频率才能保证索力计算的精度，与其他几种方法相比，其索力计算精度较差.

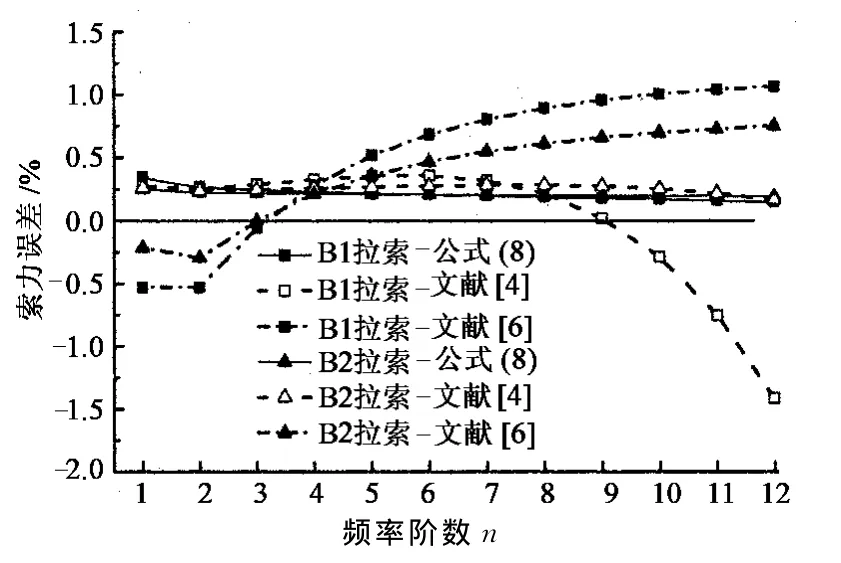
图8 B1，B2拉索索力计算误差Fig.8 B1and B2cable tension calculation error

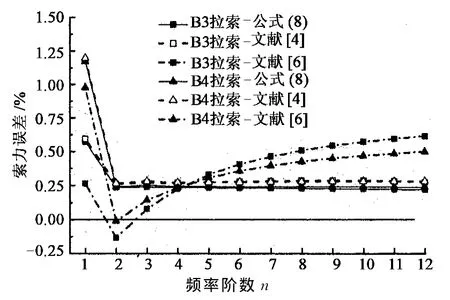
图9 B3，B4拉索索力计算误差Fig.9 B3and B4cable tension calculation error

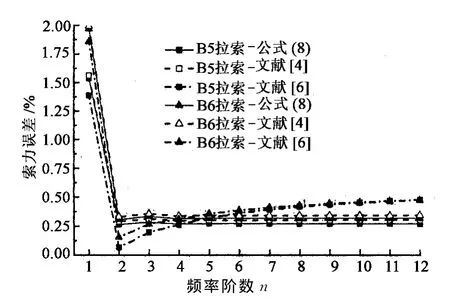
图10 B5，B6拉索索力计算误差Fig.10 B5and B6cable tension calculation error

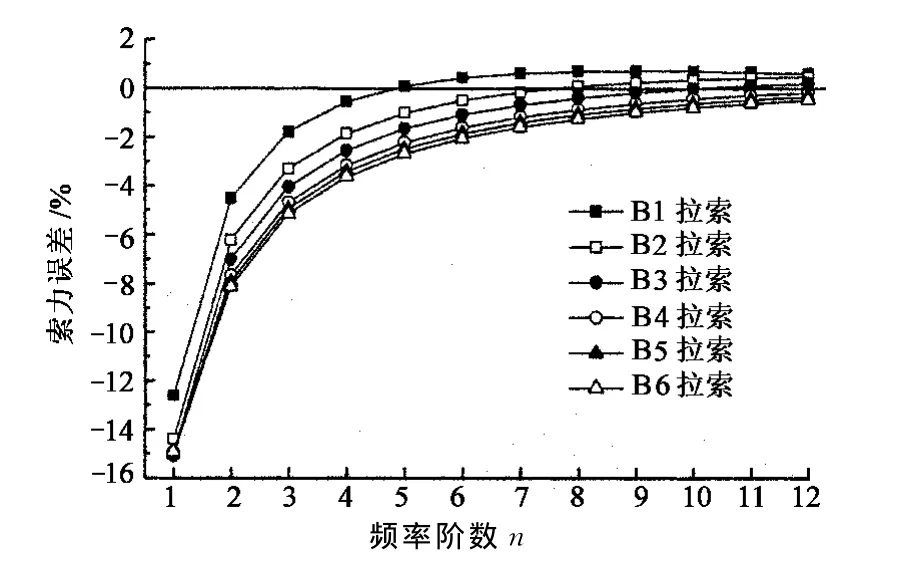
图11 文献［11］索力计算误差Fig.11 Cable tension calculation error of reference［11］

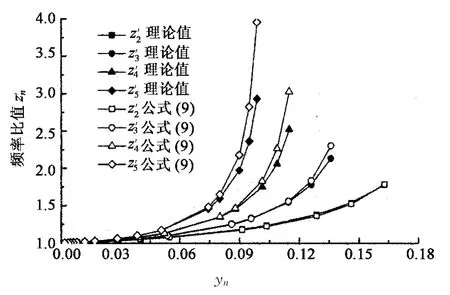
图12 拉索关系曲线Fig.12 The relationship curves of

上述分析中拉索的抗弯刚度EI已知，而实际工程中，EI不易事先准确地计算得到，为此，不少学者对抗弯刚度EI的识别方法进行了研究［13－14］.

由于本文索力计算方法采用不同阶数频率计算的索力结果基本一致（长索基频计算结果除外），因而，当获得多阶频率值时，可直接对EI和索力进行识别，即先假定EI，然后由式（8）计算各阶频率的索力，若索力基本一致，则该EI值即为实际EI值.采用1～4阶频率对A1，A3，A5吊杆进行了识别，此外，还采用2～11阶实测频率对文献［13］中3根实桥拉索进行了参数识别.文献［13］中拉索基本参数见表3，识别结果见表4，表中索力识别值为平均值.由表可知，EI和索力的识别结果都比较好，表明本文方法具有良好的适用性.

公式（8）基于拉索两端的边界条件为固结的情况，实际上拉索的边界介于简支与固结之间，如图13所示，当两端的转动约束刚度k足够大时，可视为固结边界，当k＝0时，为简支边界.

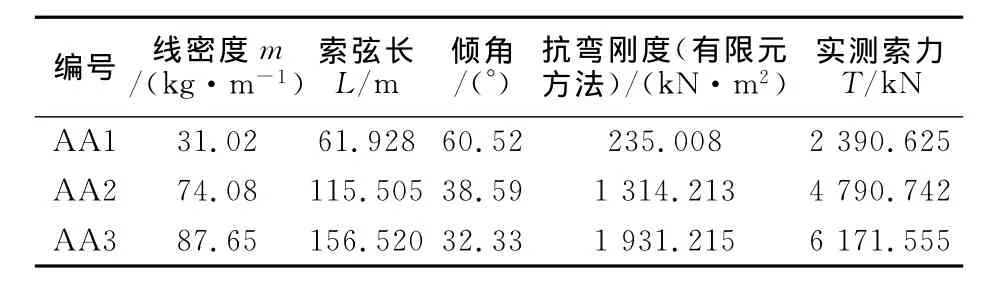
表3 文献［13］拉索参数Tab.3 Ref.［13］parameters of cables

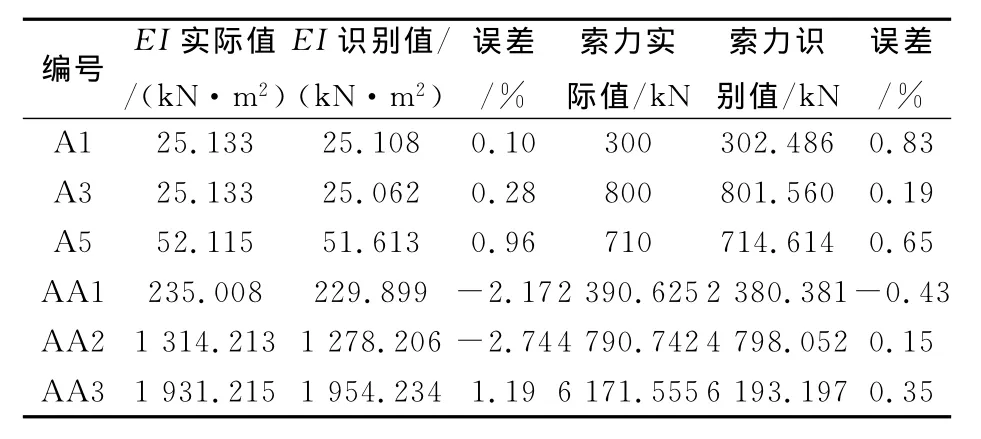
表4 抗弯刚度EI和索力识别结果Tab.4 Results of identified EI and cable tension

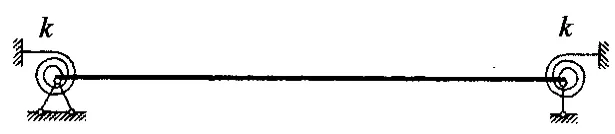
图13 拉索端部支撑Fig.13 Cable end support

记吊杆的真实索力为Tr，由简支边界计算的索力为T1，固结边界计算的索力为T2，简支、固结2种边界条件计算的索力误差分别记为e1，e2，em为二者的绝对值较小者，反映在不同约束刚度k下，吊杆边界按简支或固结处理时，可以获得的最小索力误差，分别定义为：

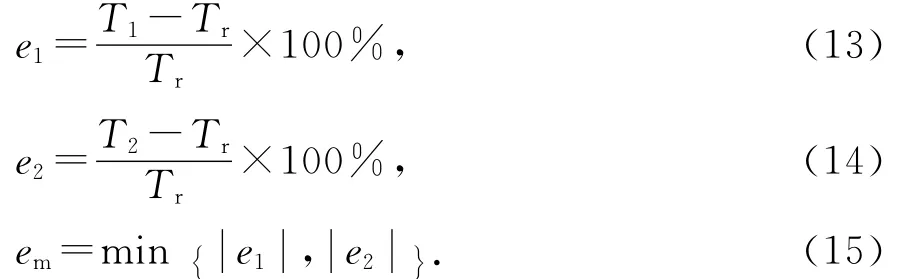
各转动约束刚度k下吊杆的频率由有限元模型计算得到.吊杆k与em的关系如图14所示（基频结果），在k＝1×104～3×106N·m／rad时，按简支或固结边界计算的索力均有较大的误差，吊杆的ξ值越小，误差越大，因而对于短吊杆，边界对索力测试的影响较大.

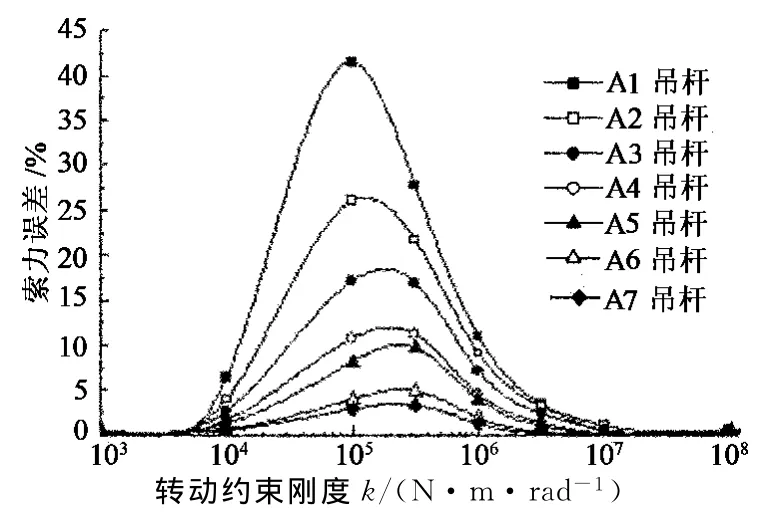
图14 吊杆k－em关系Fig.14 k－emrelationship of suspenders

观察式（7）可知，zn＝1加上一个yn的函数，当yn＝0时，zn＝1，于是引入一反映边界条件的参数ck，对yn进行拆减，拆减后记为ynk，如式（16）所示，索力计算时使用ynk代替式（7）中的yn即可.当ck＝0时，对应简支梁模型，当ck＝1时，对应固支梁模型，从而可以实现从简支状态到固结状态的连续过渡.对于吊杆不同的端部转动约束刚度k，可找到适当的ck，使索力的计算比较准确.

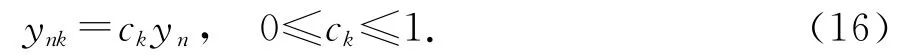
由图14可知，A6和A7吊杆的索力计算误差受边界条件的影响不大，对A1～A5吊杆，使用其前4阶频率同时识别索力T、抗弯刚度EI和边界条件影响系数ck，结果分别如图15～图17所示.由图可知，当k＝1×105N·m／rad时，A1吊杆的索力识别误差为9.2%，尽管还比较大，相对于em＝41.5%，索力误差明显减小.此外，当k＞1×106N·m／rad时，由于A4，A5吊杆识别的ck值比1偏小较多，导致其索力计算误差稍大，为6.1%，其他情况索力误差均小于5%.吊杆EI的识别误差小于7%，因而采用引入系数ck的方法可以较好地考虑边界条件对索力计算的影响.

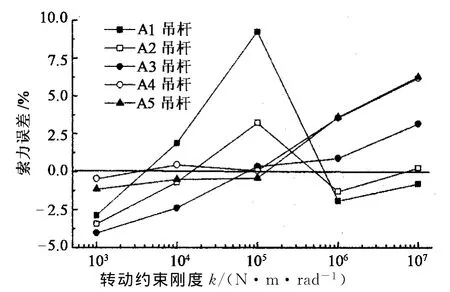
图15 吊杆索力计算误差Fig.15 Cable tension calculation error of suspenders

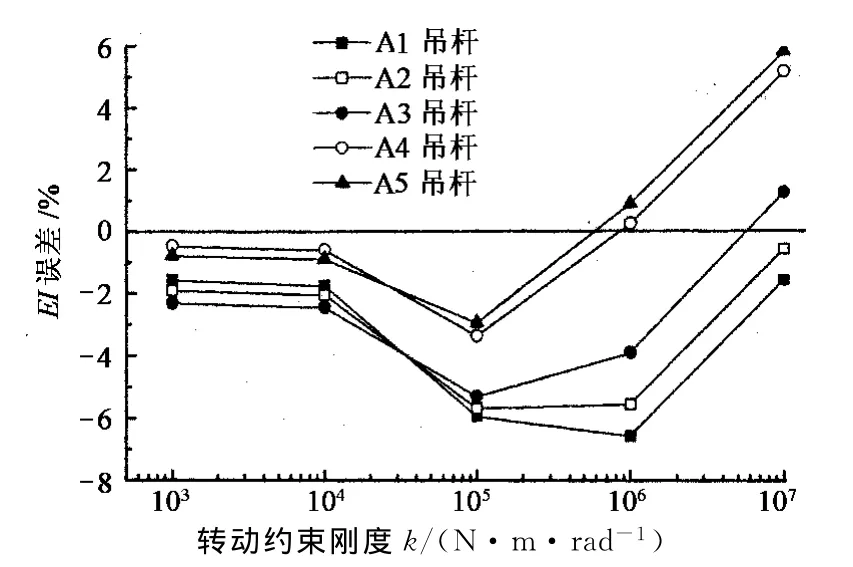
图16 吊杆EI计算误差Fig.16 EIerror of suspenders

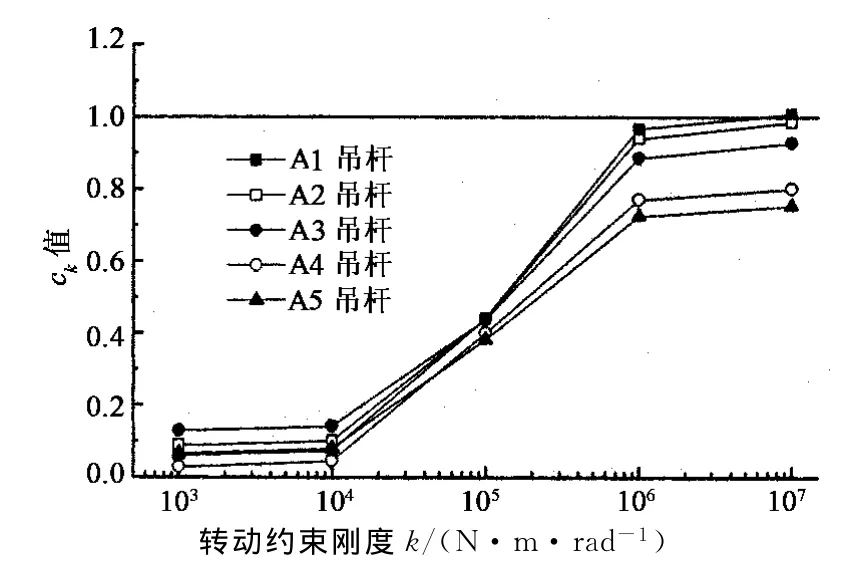
图17 吊杆ck计算值Fig.17 ckvalue of suspenders

转动约束刚度k从0增加到无穷大，相对于简支状态吊杆频率增加，将频率增加最大百分比化为1后记为归一化频率变化.构造ck的计算公式见式（17），式中β为待定函数，当β分别取常数1×105，5×105N·m／rad时，A1吊杆ck的计算值与基频的归一化频率变化比较如图18所示.由图可知，3条曲线基本平行，因而ck可采用式（17）的形式进行计算.

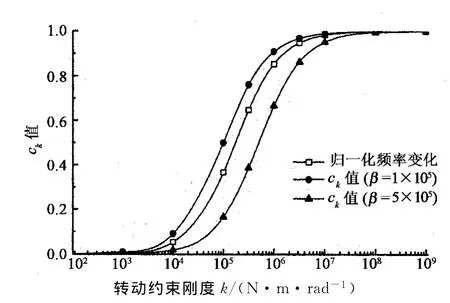
图18 ck值和归一化频率变化比较Fig.18 ckvalue compared with normalized frequency variation

β的量纲和k一致，通过分析确定ck按式（18）进行计算，式中a为待定常数，反映拉索参数对边界约束的影响，相同k值下ck随EI和T的增加而减小，即相同转动约束刚度下，拉索的刚度越大、索力越大，边界约束相对越弱.

取T按弦理论公式进行计算，对各吊杆不同k值的索力进行计算，确定式（18）中的a＝0.84，于是ck可按式（20）计算，各吊杆基频率不同k值计算的索力误差分别如图19所示.由图可见，索力误差均小于1%.

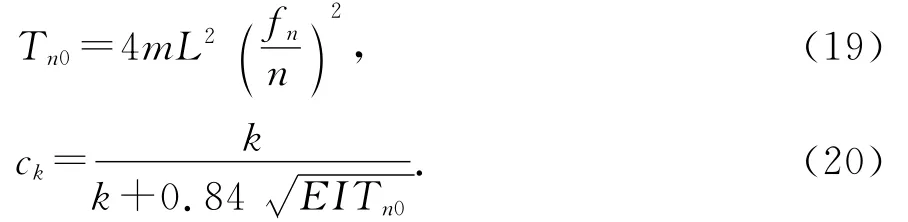
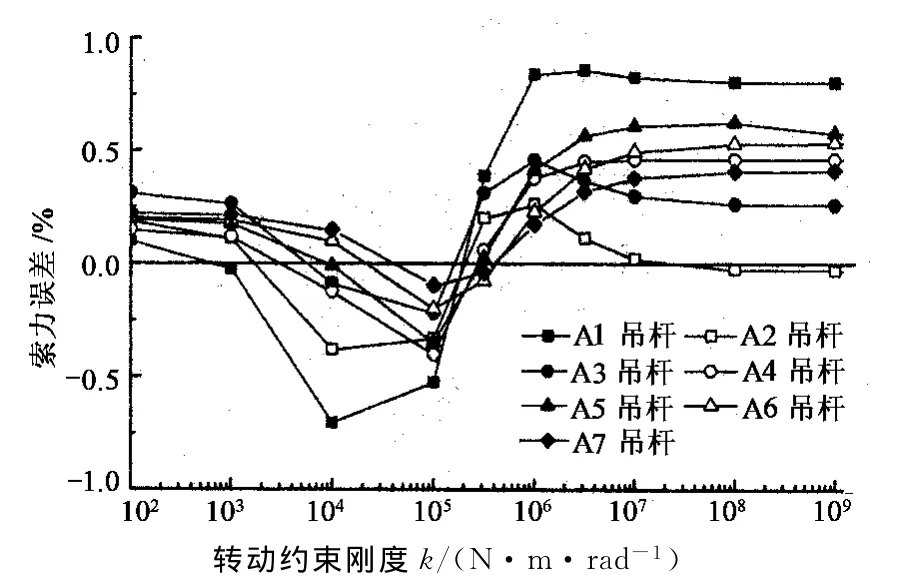
图19 吊杆索力计算误差Fig.19 Cable tension calculation error of suspenders

因而，实际使用时，第1次可按参数识别方法计算ck，再由式（20）计算出k值，或者按有限元方法精确地识别出k和EI值，之后索力计算按式（20）计算ck对yn进行拆减.

3 结 语

1）通过两端固结梁和两端铰接梁的频率特征方程，在找出二者的频率关系后，建立了一个形式简单、物理意义明确的索力计算公式.分析结果表明，该公式具有良好的计算精度和适用范围，能准确地计算ξ≥6.9的吊杆和拉索的索力，并可以用于参数识别，方便应用于实际工程中的索力测试计算.

2）分析了吊杆边界条件对索力计算结果的影响，提出了考虑端部转动约束刚度的索力计算方法，可以较精确地对吊杆索力进行计算.

［1］ NI Y Q，KO J M，ZHENG G.Dynamic analysis of large－diameter sagged cables taking into account flexural rigidity［J］.Journal of Sound and Vibration，2002，257（2）：301－319.

［2］ 郑罡，倪一清，高赞明，等.斜拉索张力测试和参数评估的理论和应用［J］.土木工程学报，2005，38（3）：64－69.ZHENG Gang，NI Yi－qing，GAO Zan－ming，et al.Theory and implementation of tension testing and parameter estimation of stay－cables［J］.China Civil Engineering Journal，2005，38（3）：64－69.（In Chinese）

［3］ KIM B H，PARK T.Estimation of cable tension force using the frequency－based system identification method［J］.Journal of Sound and Vibration，2007，304（6）：660－676.

［4］ ROBERT J L，BRUHAT D，GERVAIS J P，et al.The measurement of cable tension by the vibratory method［J］.Bulletin De Liaison Des Laboratoires Des Ponts Et Chaussees，France，1991，173（7）：109－114.

［5］ ZUI H，SHINKE T，NAMITA Y.Practical formulas for estimation of cable tension by vibration method［J］.Journal of Structural Engineering，1996，122（6）：651－656.

［6］ 方志，汪建群，颜江平.基于频率法的拉索及吊杆张力测试［J］.振动与冲击，2007，26（9）：78－82.FANG Zhi，WANG Jian－qun，YAN Jiang－ping.The tension measurement of cables and suspenders with frequency method［J］.Journal of Vibration and Shock，2007，26（9）：78－82.（In Chinese）

［7］ CEBALLOS M A，PRATO C A.Determination of the axial force on stay cables accounting for their bending stiffness and rotational end restraints by free vibration tests［J］.Journal of Sound and Vibration，2008，317（4）：127－141.

［8］ 张清华，冉志红，卜一之，等.拉索非线性振动问题求解及参数识别方法研究［J］.土木工程学报，2009，42（6）：86－91.ZHANG Qing－hua，RAN Zhi－hong，BU Yi－zhi，et al.Theory and parameter estimation for nonlinear vibration of cables［J］.China Civil Engineering Journal，2009，42（6）：86－91.（In Chinese）

［9］ 宋一凡，贺拴海，吴小平.固端刚性拉索索力分析能量法［J］.西安公路交通大学学报，2001，21（1）：55－57.SONG Yi－fan，HE Shuan－hai，WU Xiao－ping.Energy method of the tension for fixed－end rigid cables［J］.Journal of Xi′an Highway University，2001，21（1）：55－57.（In Chinese）

［10］任伟新，陈刚.由基频计算拉索拉力的实用公式［J］.土木工程学报，2005，38（11）：26－31.REN Wei－xin，CHEN Gang.Practical formulas to determine cable tension by using cable fundamental frequency［J］.China Civil Engineering Journal，2005，38（11）：26－31.（In Chinese）

［11］甘泉，王荣辉，饶瑞.基于振动理论的索力求解的一个实用计算公式［J］.力学学报，2010，42（5）：983－988.GAN Quan，WANG Rong－hui，RAO Rui.Practical formula for estimation on the tensional force of cable by its measured natural frequencies［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42（5）：983－988.（In Chinese）

［12］MEHRABI A B，TABATABAI H.Unified finite difference formulation for free vibration of cables［J］.Journal of Structural Engineering，1998，124（11）：1313－1322.

［13］李学友.大跨混凝土斜拉桥施工控制中的若干关键问题研究［D］.长沙：湖南大学土木工程学院，2009.LI Xue－you.Study on some key issues in construction control of long－span concrete cable－stayed bridge［D］.Changsha：College of Civil Engineering，Hunan University，2009.（In Chinese）

［14］苏成，徐郁峰，韩大建.频率法测量索力中的参数分析与索抗弯刚度的识别［J］.公路交通科技，2005，22（5）：75－78.SU Cheng，XU Yu－feng，HAN Da－jian.Parameter analysis and identification of bending stiffness of cables during tension measurements by frequency method［J］.Journal of Highway and Transportation Research and Development，2005，22（5）：75－78.（In Chinese）