基于GPU的并行APSP问题的研究
张凌洁,赵 英
(北京化工大学 北京 100029)
最短路径问题是图论中的一个典型问题,已经得到广泛的研究和应用。此问题包含两类:1)单源最短路径(SSSP,Single Source Shortest Paths),求给定始末顶点之间的最短路径,如旅行商问题;2)所有顶点间最短路径(APSP,All Pair Shortest Paths),求图中所有顶点对之间的全部最短路径。
目前针对此问题的相关研究成果已被广泛应用于众多领域,如城市物流规划、图形学图像分割等。由此可见最短路径问题不仅具有较高的科研意义,还具有相当高的实际应用价值。
另一方面,当今社会已步入信息化时代。海量数据以及复杂的科学计算都对计算机处理能力提出了更高的要求。HPC已经成为热点研究问题。其中GPU作为低成本低功耗的新型高性能技术得到广泛关注和长足的发展。尤其是在CUDA平台出现后,打破了图形处理编程与普通编程之间的壁垒,对于GPU的发展可谓是如虎添翼,使得更多的程序员跨入到GPU通用计算的研究当中[1-2]。
在GPU成为研究热点的背景下,利用其高性能和低成本的优势,通过对APSP最短路径并行算法的研究,解决Floyd算法在GPU并行化中产生的问题。并根据GPU特点,提出相应改进策略,从而进一步加快计算速度。希望将来可以把研究成果运用到如物流配送中心的选址,城市规划等实践中。
1 Floyd-W arshall算法简介
APSP问题就是求解给定图中所有顶点对之间的全部最短路径。此问题有两种解法:
第1种解法是,每次以一个顶点作为起始顶点,依次将其他顶点作为终止顶点求它们之间的最短路径,然后更换起始顶点,依次再求其他顶点间的最短路径。如果对每对顶点之间都使用Dijkstra算法,则总的时间复杂度将是O(n4)。
第2种解法是Floyd-Warshall算法,也称传递闭包算法。假定一张带权的有向图 G,包含 n个顶点{Vi,1≤i≤n},及 m条有向边,有邻接矩阵Arcs和初始距离矩阵 D(-1)。串行的Floyd Warshall算法的计算步骤如下:
1)初始化:初始化邻接矩阵D,如果Vi和Vj之间存在直达路径,则将D(-1)[i][j]的值设为路径长度;如果不存在直接路径,则 D(-1)[i][j]的值设为 ∞。 注意,默认情况下,顶点到顶点自身的路径长度为0;
2)依次计算 D(k)[i][j](k=0,1,…n-1)中 D[i][j]的值,如果经过中间顶点 Vk,D[i][k]+D[k][j]的值小于D[i][j],则表明经过顶点k存在更短路径,更新D[i][j]值,直至图中的所有顶点都做过中间顶点得到最后的D矩阵。
使用Floyd-Warshall算法的串行版本去处理ASAP问题,在数据规模比较小的时候,由于逻辑简单,还是非常实用的。然而,算法主体是三重循环,使得当数据规模随着图中顶点数量增大的时候,算法的执行时间也将呈现指数级的增加,在处理现实问题时效果并不理想。
2 基于GPU的Floyd算法的并行化
Floyd-Warshall串行算法的核心是一个三重循环的迭代计算,算法的时间复杂度是O(n3)。如果将算法并行化,将极大的缩短计算时间[5]。对于三重循环体的处理,类似于GPU芯片对矩阵乘法的计算过程。所以,可以将循环体内的比较权值的操作改为CUDA多线程并行执行。实现多线程并行后可以大大提高计算速度,发挥GPU并行计算的优势。
该并行化算法的原理如下:首先选取距离矩阵中主对角线位置的元素作为Key,在n×n距离矩阵中共有n个Key,其坐标值为(0,0),(1,1)…(n,n)。 每次迭代选取一个 Key 作为基准,选出与Key共行或共列的元素作为参考值,计算余下(n-1)×(n-1)个元素。每个元素 c计算时,从参考值中找到和本元素共行的元素a,和参考值中与本元素共列的元素b,判断a+b与c的大小关系。如a+b更小,则更新该元素值为a+b;否则,不更新。计算完本轮的(n-1)×(n-1)个元素后,Key元素沿对角线向下移动,按上述步骤重新计算。图1展示了计算元素与参考元素的位置关系。
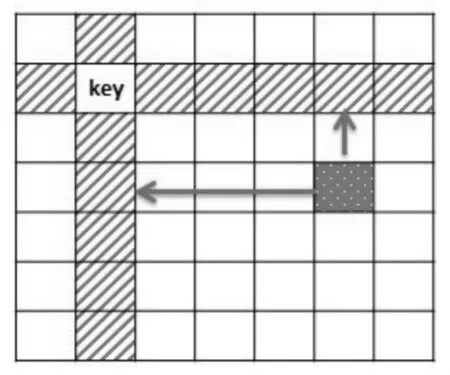
图1 距离矩阵计算时元素对应关系Fig.1 Relationship of elements in distancematrix
GPU并行程序的重点就是线程的分配和核函数(Kernel Function)的设计[3]。首先介绍如何通过核函数完成多线程的并行计算。并行化的Floyd-Warshall算法中使用到了以下几个核函数:
1)初始化核函数:根据邻接矩阵的值初始化距离矩阵中的权值。这里需要注意线程的对应关系,将邻接矩阵等价为一维数组,依次复制其中的值到grid中,并赋值给距离矩阵。所以每个线程在循环处理中的增量大小为整个grid中线程的个数。
2)计算核函数:计算距离矩阵中每个元素位置对应的最短路径。距离矩阵中的每个元素都与主轴上对应的同行和同列的两个元素的权值之和做比较。如,Dij表示顶点i到顶点j的路径权值,需要和Dik+Dkj的权值作比较,其中Dik与Dij同行,Dkj与Dij同列,而k表示当前迭代时是以顶点k作为中间顶点。
下面介绍线程的分配。这时会遇到下面的两种情况:当要处理的矩阵小于或等于grid的大小,那么在线程在计算相应的顶点权值的时候,需要首先对是否在边界当中进行判断。如果在边界当中,则继续进行处理和计算,反之,则放弃计算;当要处理的矩阵规模大于grid中线程个数时,需要计算其相对位置,分批次计算,如图2所示。

图2 距离矩阵计算时线程对应关系Fig.2 Relationship of threads on grid, block and computing distancematrix
当距离矩阵规模较大时,根据线程数分块和相应的映射原则,将数据交由GPU的grid计算。GPU属于两层并行结构,其中每个grid中含有多个block,每个block又含有多个线程,上图中左侧的两个图就表示了这个关系[4]。当grid中的线程数不足以为每个矩阵元素分配线程时,需要按照grid的大小将原距离矩阵分块,依次分配给grid计算。在上面最右侧的图片中,1号子矩阵分配给grid计算完成后,再将2号子矩阵分配给grid计算,然后是3号子矩阵。注意,这里距离矩阵的大小并不能正好整除grid的大小(7%3!=0),所以3号子矩阵的元素个数比较少,可以分配给grid计算,剩余部分不做计算。以此类推,向左向下继续计算各个子矩阵。这里使用相应的行偏移和列偏移变量去表明GPU上grid应该对应的距离子矩阵的方位。
3 Floyd-W arshall并行算法的改进
在上一节中,已经实现了基于GPU的并行的Floyd-Warshall算法,但是为了进一步提高程序的计算效率,可以利用GPU当中的共享内存对程序进行改进。这里借用了Venkataraman提出了一个更复杂的、基于 “块”的Floyd的APSP算法[7]。对于大规模的图而言,这个算法可以更好的利用缓存,并提供了更加具体的性能分析。在课题研究过程中,对这个的应用进行了扩展,使其通过CUDA平台运行在GPU上,并获得更高的效率。原始的F-W算法并不能够拆分成相互之间无关联的子矩阵,然后分给GPU上的每一个处理器来分开计算。其原因就在于每一个子矩阵需要和整个数据集产生对应关系。查看F-W算法串行,可以发现D矩阵中的每个值的更新都需要检查矩阵中的其他的每一个数据。所以想要简单地拆分矩阵并不是可行的。但是,通过仔细选择的一些子矩阵序列,就可以解决这个问题。而这个分块的F-W算法就是使用之前处理过的某些子矩阵去决定现在正需要处理的子矩阵,这就使得问题并行化成为可能。
算法首先需要对距离矩阵进行分块,而划分完成后,就可以开始分阶段进行计算了。矩阵主模块个数等于迭代的次数[7]。以下以6×6的矩阵为例,对这个算法进行简要地介绍。首先如下图将这个矩阵分出3个主模块(主对角线上的3个子矩阵),所以就产生了3次迭代。每个阶段根据自己的主模块来运算,算法的每一阶段都分为同样的3步计算。

图3 分块F-W算法过程演示Fig.3 Example of GPU-Tiled-FW parallel computing
步骤1:只计算主模块中的最短路径,观察是否仅仅经由主模块所包含的顶点能够获得更短的路径。此时将主模块分配给CUDA中的一个block去计算,所以此步骤只需要用到了一个多处理器。主模块就是当前需要计算的模块,所以除了主模块本身,不在需要加载任何其他数据到共享存储器(Shared Memory)。每一个线程可以直接加载它们的线程编号对应的数据块,并在这一阶段的计算结束后,将结果保存到全局存储器(Global Memory)中。如图4所示,为当第2个主模块为当前主模块时进行步骤一时的情形。
步骤2:计算那些只依靠自己和相应主模块来运算的子模块,即与主模块在同一行和同一列的模块。此时,主模块和当前计算模块都需要加载到共享存储器中,这就使得GPU中每一个线程都能从block的共享存储器中加载到一个对应的单元。同样,在此阶段完成后,需要每个线程将数据传回到全局存储器中。如图4(b)所示,为当第2个主模块为当前主模块时进行步骤2时的情形。
步骤3:计算剩余的子模块,如图4所示,当以7号模块为主模块的计算到达步骤3时,只有1、2、3、4号模块需继续计算。也就是说,当完成步骤1和步骤2时,还要处理剩下的(n-1)×(n-1)个子模块。此时需放入共享存储器中的模块除了自己之外,还需要将以当前主模块为轴的同行和同列对应的模块一并载入到共享存储器当中。如图4(c)所示,为当第2个主模块为当前主模块时进行步骤3时的内存分配情形。
完成上面3个步骤,沿对角线向下移动主模块,重复上面的计算步骤。直至全部主模块都计算后,才算完成依次迭代。再进行第二次迭代,比较两次迭代后的距离矩阵:如果经过后一次迭代,距离矩阵并未发生变化,则迭代结束;否则,进行新一轮的迭代,直至距离矩阵不再发生改变。
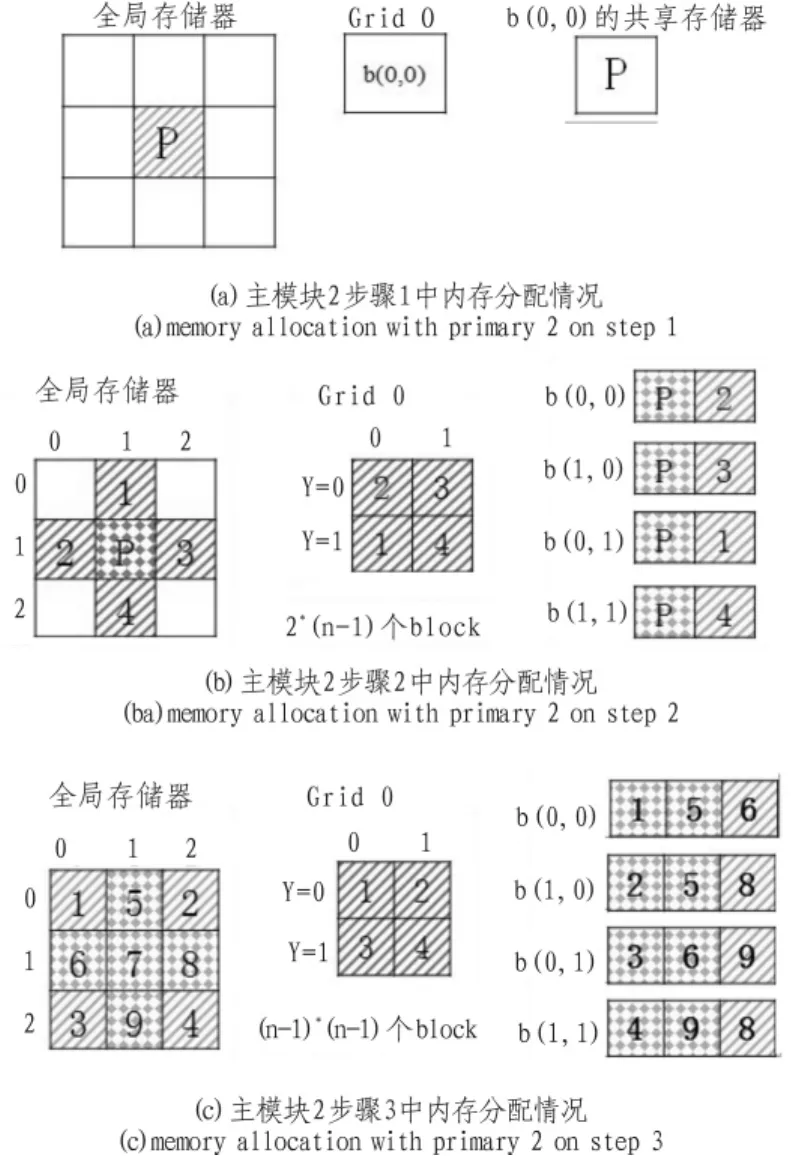
图4 内存分配情况Fig.4 Memory allocation
4 实验结果比较与分析
文中所有的程序运行的硬件平台为惠普公司的ProLiant系列SL390s G7服务器。其中每个节点服务器都由两个2.4-GHZ的英特尔Xeon系列E5620处理器以及24 GB大小的内存和两块NVIDIA的Tesla系列M2050的GPU构成。本课题的软件平台为 64位 Linux RedHat 6.0操作系统,NVIDIA Tesla 驱动器,CUDA SDK 3.2,CUDA Toolkit 4.0。 所以的程序运行数据都是在上述平台上运行15次取平均值获得的。
从表1的数据和性能比较图中可以看出,无论是原始的GPU并行F-W算法还是之后改进的分块的并行F-W算法,当数据规模较小时(≤100)时,算法执行时间维持在一个较低的水平,大概在3 s左右。而且从图中也无法看出改进的GPU并行程序优越于原始的并行程序,可以认为它们是相当的。而串行的CPU版本的F-W算法却极其出色的完成了任务,基本在0.5 s内就完成计算。这可能是由于在GPU并行算法当中,需要进行GPU设备与主机内存之间的数据传输,而这个传输是非常耗费时间的,且由于计算规模太小,使得这一瓶颈突显出来。
对于改进的GPU并行F-W算法来说,也是由于较小的计算量,使得算法中的分块以及加载使用共享存储器并没有显现出优势,所以使用两种并行算法在效率上没有什么分别。另外,值得注意的是,可以从图5(a)中看到,串行版本的F-W算法在数据增加的后期,已经开始发生明显地时间增加,尽管增加的绝对值并不大。

表1 光顶点数≤100的Floyd算法串行程序和GPU并行程序耗时比较Tab.1 Cost time comparison with less than 100 vertices on CPU,GPU,and Tiled-GPU
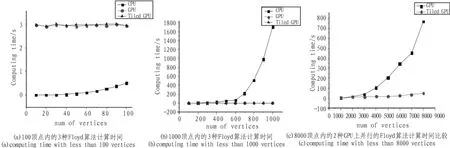
图5 算法计算时间Fig.5 Computing time

表2 光顶点数≤1000的Floyd算法串行程序和GPU并行程序耗时比较Tab.2 Cost time comparison with less than 1000 vertices on CPU,GPU,and Tiled-GPU
表2的数据表示了在顶点数为100~1 000,间隔为100的输入数据下,各种F-W算法计算时间的比较。首先从表2中,可以看出两种GPU并行F-W算法在计算时间上只有相对较小幅度的增加,即从3 s左右的计算时间增加到了5 s左右。而且在顶点数大于等于700时,改进后的分块GPU并行F-W算法才稳定地表现出了一些优势,尽管这个优势并不大。而CPU版本的串行程序的运行时间在这个阶段却产生了指数级的增长,这使得在图5(b)中,GPU并行算法和GPU分块并行算法的计算时间几乎和坐标轴平行。
表3的数据可以看出,在这个阶段CPU对F-W算法的计算时间已经超出需求范围,这使得在图5(c)中,并没有出现串行版本的执行时间曲线。很显然,由于算法中的一个二维循环和一个三维循环,使得在这个阶段,每一次的数据增加都会带来迭代次数的“暴增”。而原始的GPU并行F-W算法也因为顶点数的增加,使其自身的迭代次数和循环处理次数增加。而且这一算法是直接读取全局内存中的数据,这种延迟也会累积到一个可观的数值的。相对而言,改进的分块GPU并行F-W算法的计算时间增加就小得多。尽管这种算法当然也会因为顶点数的增加,使其迭代次数增加,但是由于使用了共享存储器的优化,且访问共享存储器是访问全局内存的若干倍,这使得迭代次数的增加被访问的加速而掩盖,进而达到了令人满意的并行效果。

表3 光顶点数≤8000的Floyd算法串行程序和GPU并行程序耗时比较Tab.3 Cost time comparison with less than 8000 vertices on CPU,GPU,and Tiled-GPU
5 结 论
文中针对APSP问题中的Floyd-Warshall算法的并行化进行了较为全面的研究和分析。实现了基于GPU的并行的Floyd算法,在数据规模超过100个顶点后,加速比平均达到100倍以上。然后又利用GPU架构中的共享储存器,根据Venkataraman提出的分块思想,将上述GPU并行算法进行优化。进一步优化之后,加速比达到8倍以上,计算速度明显加快。
在后续的研究中,希望可以将GPU版本的并行F-W算法应用在多GPU上,得到更高的性能加速比。并将这一并行算法应用到实际中,如物流中心的选址、城市规划等问题当中。
[1]许桢.关于CPU+GPU异构计算的研究与分析[J].科技信息,2010(17):22-28.
XU Zhen.Research and analysis of CPU+GPU heterogeneous computing[J].Technology Information,2010(17):22-28.
[2]张舒,褚艳丽,赵开勇,等.GPU高性能运算之CUDA[M].北京:中国水利出版社,2009.
[3]Harish P,Narayanan P J.Accelerating large graph algorithms on the GPU using CUDA[J].High Performance Computing-HiPC,2007:197-208.
[4]程豪,张云泉,张先轶.CPU-GPU并行矩阵乘法的实现与性能分析[J].计算机工程,2010(7):24-25.
CHENG Hao,ZHANG Yun-quan,ZHANG Xian-yi.Implementation and performance analysis of CPU-GPU parallelmatrix multiplication[J].Computer Engineering,2010(7):24-25.
[5]Nvidia:Cuda 3.0.Technical report,Nvidia Corp.(2010) Available at[EB/OL].http://developer.nvidia.com/object/cuda_3_0_downloads.htm l.
[6]卢照,师军.并行最短路径搜索算法的设计与实现[J].计算机工程与应用,2010(46):69-71.
LU Zhao,SHIJun.Design and implement of parallel computing of shortest paths[J].Computer Engineering and Applications,2010(46):69-71.
[7]Venkataraman G,Sahni S,Mukhopad H S.A blocked all-pairs shortest-pathsalgorithm[M].J.Exp.Algorithmics,2003.

