深海系缆动张力的超谐动力响应
张若瑜,唐友刚,宋吉哲,刘利琴
(1天津大学建筑工程学院暨港口与海洋工程教育部重点实验室,天津300072;2中国船级社天津分社,天津300457)
1 引 言
Spar平台主体在风浪流的作用下一旦遇到极端海况,则会引起平台发生大幅运动,一般认为,平台浮体运动是引起系泊系统缆索动张力的主要原因。因此考虑平台主体运动分析系泊系统的动力响应是十分重要的。Aamo[1]建立了在水中悬挂缆索有限元模型,用Morison公式计算缆索受到的水动力,忽略缆索附加质量,推导出了两端固定的系缆运动方程,给出系统整体解的存在性和唯一性。Huang[2]用单自由度模型计算松弛张紧条件下系缆—浮体系统在垂荡运动下的动力特性。Chen[3]基于细长杆理论用有限元方法建立了深海系泊系统模型,研究了系泊系统与平台主体之间的动力相互作用。Kim[4]用等参曲线索单元计算几何非线性有限元方程,求出单元切线刚度矩阵和质量矩阵,用罚函数法和载荷增量法确定初始平衡点,最终得到在水流,规则波和不规则波以及精确计算Morison力对海中缆索的作用。张素侠[5]综合考虑系泊缆绳和系泊浮体的相互耦合作用以及缆绳的粘—弹特性,根据冲击动力学理论建立缆绳—浮体系统冲击之后和冲击之前的运动方程,计算了不同参数条件下系泊缆索的动力响应。Sarkar[6]研究了在随机波浪激励下系泊浮体的非线性动力响应,并且在频域内分析了由于海上平台随机运动引起的悬链系泊索的动力特性。杜度[7]应用时域仿真的方法研究了系泊系统的非线性动力学特性。以三阶操纵运动方程为基础,引入定常的风力、潮流作用力和二阶波浪力,建立了系泊系统三自由度的运动微分方程。并在此数学模型的基础上,建立了系泊系统的多自由度的计算机仿真模型。研究表明,系泊系统的动力学行为具有强烈的非线性特征。向溢[8]对系泊船舶缆绳张力的计算建立了数学模型。用蒙特卡洛算法对系泊非线性方程组进行了求解。该方法可用于求解船舶在风、浪、流联合作用下缆绳的静张力。肖越[9]采用在频域内对浮体运动方程求解并将计算结果转换为时域结果,同时与锚链线运动时域方程耦合求解锚泊浮体在限制工作水深的运动位移与锚链线上的张力。
目前对于缆动张力的研究,大部分基于单根缆的动张力分析,对于系泊缆群的动力响应计算,目前研究工作还很少。本文基于细长杆单元模型,考虑深海系泊索单元的几何非线性,并且引入单元内张力一致假设,建立三维非线性细长杆单元刚度矩阵,并且实现与通用有限元软件ABAQUS对本文单元的调用,研究具有数根系泊缆的系泊系统的动力响应特性。
2 细长杆模型的基本理论
在细长杆理论中,细长杆的形态是由其中心线位置表述的。杆的中心线则由空间曲线r s,( )t表示,如图1所示,其中s为弧长,t为时间。曲线上任意点的单位切向量为r′,单位主法向量为r″,单位副法向量为r′×
模型单位弧长分段的力和弯矩的平衡方程可以写为以下形式:

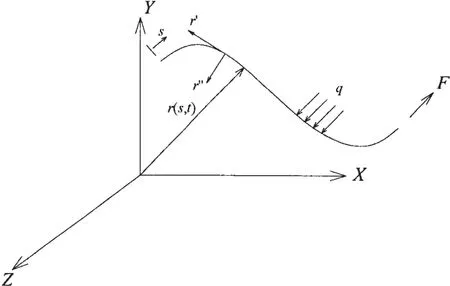
图1 细长杆模型坐标系Fig.1 Coordinate of rod
其中,q为单位长度上的外力,F为轴线上合力,M为轴线上合弯矩,ρ为单位长度质量,m为单位长度上施加的弯矩,向量r上方的点“.”表示对时间求导,′表示对弧长s求导。对于等主刚度柔性杆,弯曲刚度沿副法线方向并且与曲率成正比,写为:

由于缆索可伸长,设伸长条件为:

对于大多数海洋结构物而言,杆件(如系泊缆、立管及张力腿)上的外载荷是由周围流体的静水压力、水动力以及自重引起的,因此(1)式中的q可以写为:

其中,w为空气中缆单位长度的重量,Fs为单位长度静水压力,Fd为单位长度水动力,由莫里森方程求得。最终得到在自重、静水压力和水动力联合作用下缆索的方程有限元形式,写为:

将(18)式和(19)式分别写成一般二阶微分方程和代数方程形式:

由(20)式可以看出,Mijlk为一般质量项,为附加质量项,为由弯曲刚度EI产生的刚度,为由缆索曲率及拉伸产生的刚度。对于二维问题,i,j=1,2;而三维问题 i,j=1,2,3;并且下标 l,k,s,t=1,2,3,4。或将(20)式和(21)式合并,写成矩阵形式:

为了编写本文单元程序,使有限元软件计算结果更加稳定,减小计算规模,提高计算效率,本文假设系缆单元内部张力一致,因此将(21)式变换为:

(25)式为缆单元的动力微分方程。根据该方程,可以最终得到12×12刚度矩阵及质量矩阵,求解此方程,得到缆索单元结点动位移,再计算缆伸长量,由缆的截面几何特性计算张力。

图2 系泊系统有限元模型图Fig.2 Finite element model of mooring system
3 系泊系统上端点升沉运动时缆索的动力响应
系泊系统模型如图2所示,系缆为12根,分为四组,每组三根,为链—缆—链形式,上端为弹簧支座,以模拟由于平台垂向运动而产生的浮力变化,底端铰接,Spar平台作业水深为1 800 m。采用文献[8]系缆参数,如表1所示。

表1 系缆参数Tab.1 Parameters of mooring system
在系泊系统上端点施加最大幅值为0.086 m的垂向位移激励,变化规律如图3所示。图4为z轴运动相图。图5为系缆上端点张力历程,最大张力为2.37×106N。
从图6可以看出,张力谱包含有激励频率成分以及4.6 rad/s高频成分。

图3 系泊系统上端点垂向位移时间历程曲线Fig.3 Vertical displacement history of the upper point
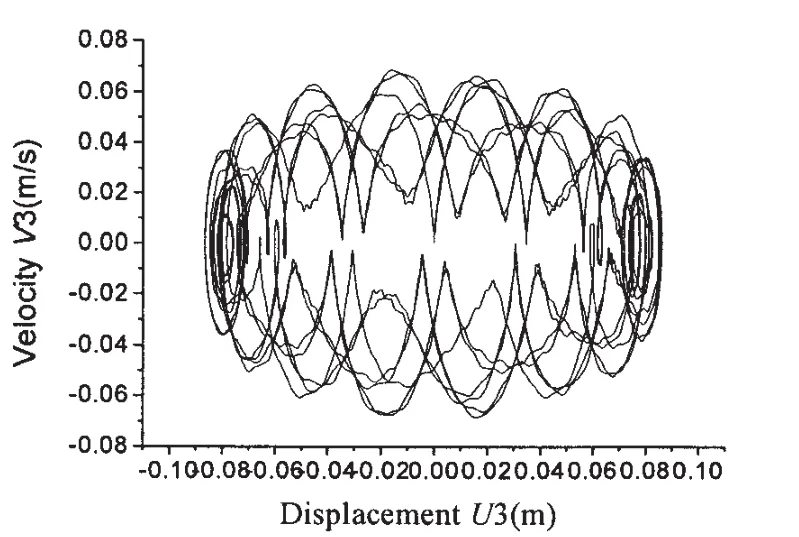
图4 系泊系统上端点垂向运动相图Fig.4 Vertical motion phase graph of the upper point
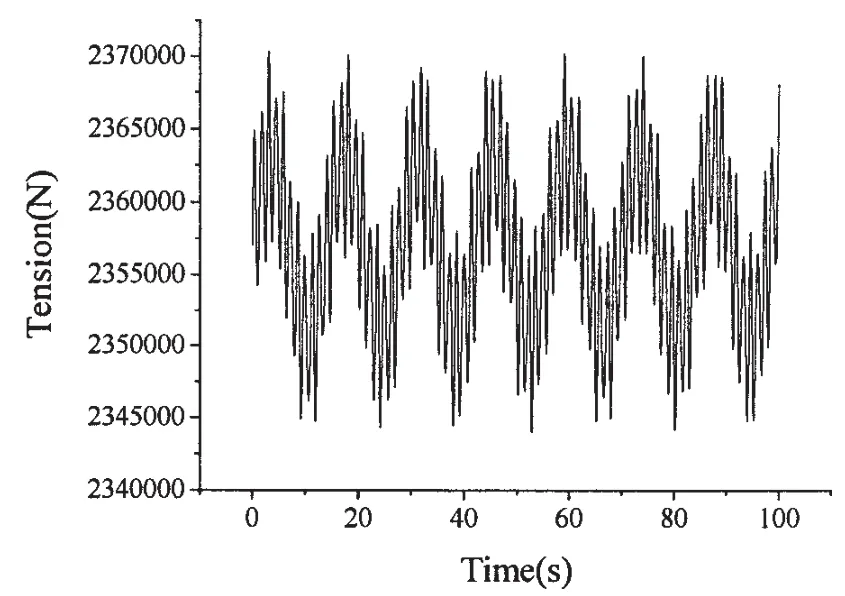
图5 系泊系统上端点张力历程Fig.5 Tension history of the upper point

图6 系泊系统上端点张力谱Fig.6 Tension spectra of the upper point
4 系泊系统上端点升沉、纵荡及水流影响时的动力响应
假设水流沿x轴正方向传播,系泊系统12根缆索布置以及x、y轴方向如图7所示,z轴为与xy轴平面垂直向上方向,即水深方向。其中编号8的缆索在水流作用下,受到的张力最大。分别计算垂荡幅值为0.089 m、纵荡幅值为2.411 m、流速为0.5 m/s,以及垂荡幅值为0.085 7 m,纵荡幅值为21.7 m,流速为1.5 m/s,系缆上端点的x、z轴方向位移、速度以及第8号缆索受到的张力。

图7 系缆布置图Fig.7 Mooring system arrangement
4.1 纵荡幅值2.411 m,垂荡幅值0.089 m,流速0.5 m/s时动力响应
流速为0.5 m/s,水流传播方向为x轴正方向,取法向拖曳力系数为1,切向拖曳力系数为0.01,取x方向位移振幅最大偏离平衡位置约2.411 m,z方向位移振幅最大偏离平衡位置约 0.089 m,变化规律如图8和9。图10及图11分别为系泊系统上端点x轴方向及z轴方向相图。其中,x轴方向最大速度为1.42 m/s;z轴方向最大速度为0.243 m/s。图12和13分别为8号系泊索上端张力历程及对应的频谱图,其中最大张力为2.604×106N。
从图13可以看出,与不考虑水流作用时相比,系缆张力谱除了激励频率成分,还出现了2倍激励频率成分,高频成分也有所变化。

图8 系泊系统上端点x方向位移Fig.8 Displacement in x direction of the upper point

图9 系泊系统上端点z轴方向位移Fig.9 Displacement in z direction of the upper point

图10 系泊系统上端点x轴方向运动相图Fig.10 Phase graph in x direction of the upper point

图11 系泊系统上端点z轴方向运动相图Fig.11 Phase graph in z direction of the upper point
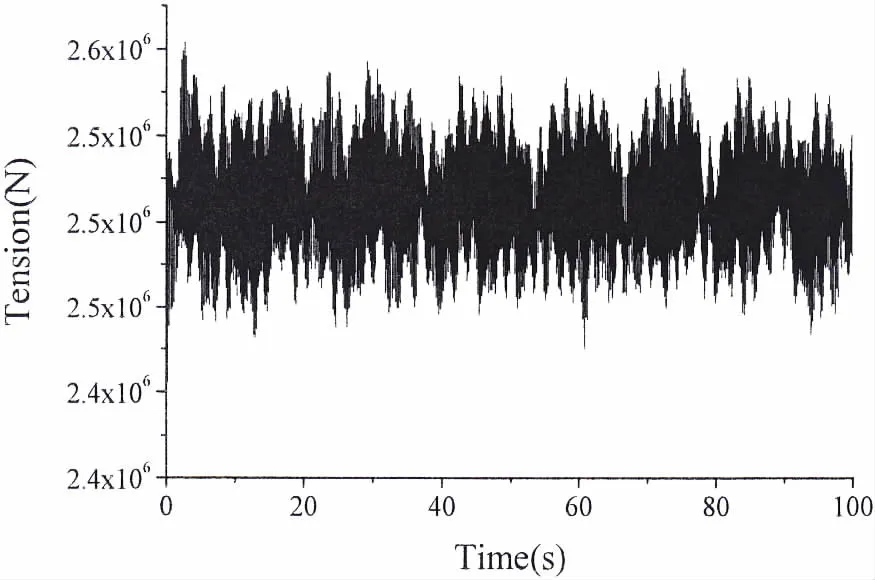
图12 8号系泊索顶端张力历程Fig.12 Tension history of the upper point for No.8 cable
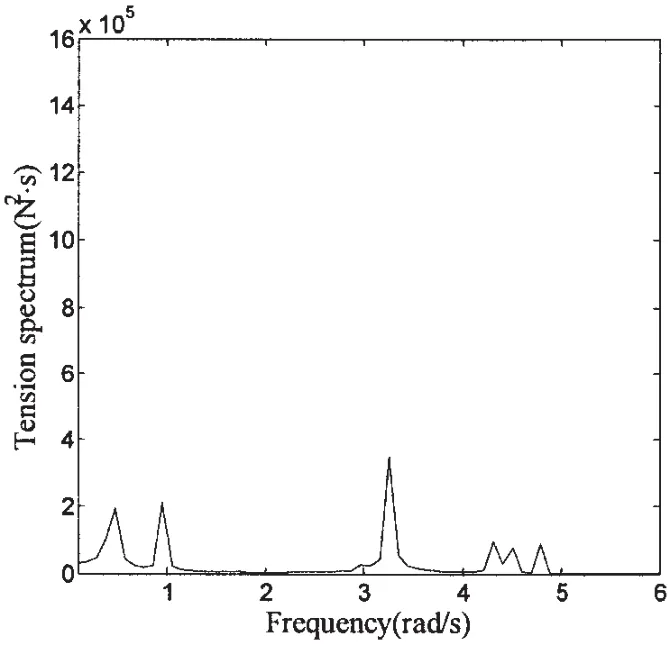
图13 8号系泊索顶端张力频谱图Fig.13 Tension spectra of the upper point for No.8 cable
4.2 纵荡幅值21.7 m,垂荡幅值0.085 7m,流速1.5 m/s时动力响应
流速为1.5 m/s,水流传播方向为x轴正方向,取法向拖曳力系数为1,切向拖曳力系数为0.01,取x方向位移振幅最大偏离平衡位置约21.7 m,z方向位移振幅最大偏离平衡位置约0.085 7 m,变化规律如图14和15。图16及图17分别为系泊系统上端点x轴方向及z轴方向相图。其中,x轴方向最大速度为17.87 m/s;z轴方向最大速度为0.236 m/s。图18和19为第8号系泊索上端张力历程及对应的频谱图,其中最大张力为3.703×106N。

图14 系泊系统上端点x方向位移Fig.14 Displacement in x direction of the upper point
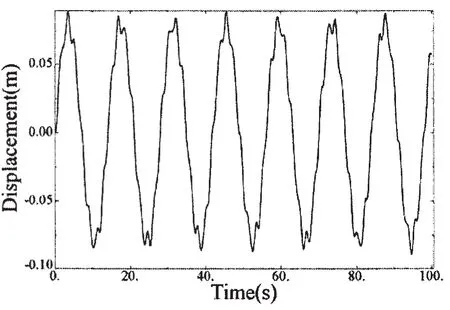
图15 系泊系统上端点z轴方向位移Fig.15 Displacement in z direction of the upper point

图16 系泊系统上端点x轴方向运动相图Fig.16 Phase graph in x direction of the upper point
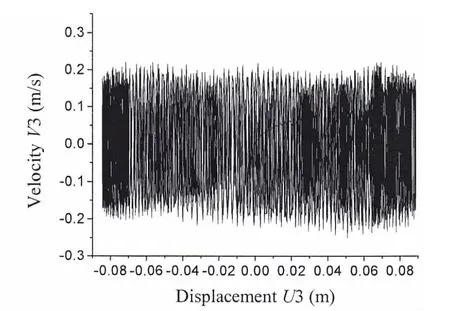
图17 系泊系统上端点z轴方向运动相图Fig.17 Phase graph in z direction of the upper point
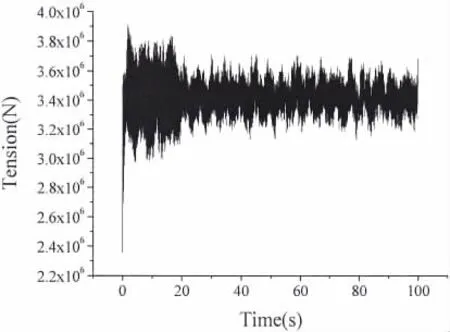
图18 8号系泊索顶端张力历程Fig.18 Tension history of the upper point for No.8 cable

图19 8号系泊索顶端张力频谱图Fig.19 Tension spectra of the upper point for No.8 cable
通过计算比较可以看出,三者垂荡幅值比较接近,仅考虑主体垂荡运动时,缆索张力幅值为2.37×106N;同时考虑系缆上端垂荡、纵荡运动和流速为0.5 m/s的海流共同作用时,缆张力幅值为2.604×106N,就此例而言,海流的影响使缆张力增加大约10%,因此在流速较低的情况下,海流的影响基本上可以忽略。当流速增大到1.5 m/s,缆张力增大为3.703×106N,这表明随着海流流速增大,流速的影响才需要考虑。在我国南海环境条件下,流速达到1.5 m/s属于一般情况,因此对于南海深水平台动张力计算,考虑海流的影响是必要的。并且比较图13与图19可以看出,随着水流速度的增加,2倍激励频率影响逐渐增大。
5 结 论
(1)在流速较低时,海流对张力幅值的影响基本上可以忽略,但是随流速增大,海流对于张力幅值影响加大。
(2)海流对于缆索的影响包括张力幅值和张力响应的频率两个方面。由于海流影响,张力谱中出现两倍激励频率成分,即出现两倍超谐共振。并且随着水流速度的增加,2倍激励频率影响逐渐增大。
(3)系缆的超谐动张力分量使得系缆张力产生高频变化,对于缆索疲劳累积损伤具有重要影响,在系缆疲劳分析时应该予以考虑。
[1]Aamo O M,Fossen T I.Finite element modeling of mooring lines[J].Mathematics and Computers in Simulation,2000(53):415-422.
[2]Huang S.Stability analysis of the heave motion of marine cable-body systems[J].Ocean Engineering,1999,26:531-546.
[3]Chen X H,Zhang J,Ma W.On dynamic coupling effects between a spar and its mooring lines[J].Ocean Engineering,2001,28(7):863-887.
[4]Kim Nam-,Jeon Sang-Soo,Kim Moon-Young.Nonlinear finite element analysis of ocean cables[J].China Ocean Engineering,2004,18(4):537-550.
[5]张素侠.深海系泊系统松弛-张紧过程缆绳的冲击张力研究[D].天津:天津大学,2008.
[6]Sarkar A,Eatock Taylor R.Dynamics of mooring cables in random seas[J].Journal of Fluids and Structures,2002,16(2):193-212.
[7]杜 度,张 宁,马 聘,张纬康.系泊系统的时域仿真及其非线性动力学特性分析[J].船舶力学,2005,9(4):37-45.Du Du,Zhang Ning,Ma Cheng,et al.Time domain simulation research on the dynamic responses and dynamic characteristics[J].Journal of Ship Mechanics,2005,9(4):37-45.
[8]向 溢,谭家华.码头系泊缆绳张力的计算[J].船舶力学,2002,6(3):20-27.Xiang Yi,Tan Jiahua.Analysis of mooring line forces of a berthed ship[J].Journal of Ship Mechanics,2002,6(3):20-27.
[9]肖 越,王言英.三维锚泊系统时域计算分析[J].船舶力学,2005,9(5):8-16.Xiao Yue,Wang Yanying.Time-domain analysis for 3-D mooring system[J].Journal of Ship Mechanics,2005,9(5):8-16.
[10]Ran Z.Coupled dynamic analysis of floating structures in waves and currents[D].Ph.D.Dissertation,Texas A&M University,2000.
[11]Arcandra.Hull/mooring/riser coupled dynamic analysis of a deepwater floating platform with polyester lines[D].Ph.D.Dissertation,Texas A&M University,2001.
- 船舶力学的其它文章
- 阻流板水动力机理的初步计算研究
- 水下滑翔机水动力外形研究综述

