硬件增强角速率圆锥优化算法的姿态解算精度分析及改进

陈建锋 陈熙源 祝雪芬

(1 东南大学微惯性仪表与先进导航技术教育部重点实验室，南京210096)

(2 江苏大学电气信息工程学院，镇江212013)

姿态解算是捷联惯性导航系统(strapdown inertial navigation system，SINS)算法中最重要的部分.高精度的姿态解算通常由圆锥优化算法和姿态四元数更新2 部分构成［1］，其中圆锥优化算法一直是SINS 研究的热点内容.

现有的圆锥优化算法都是在Bortz［2］提出的旋转矢量的基础上发展起来的.经典的圆锥优化算法采用的是基于角增量信号的多子样算法结构，适用于输出信号为角增量的陀螺仪.考虑到某些新型陀螺仪的输出为角速率信号，如果直接采用公式提取角增量，并不能体现多子样圆锥优化算法原有的优越性［3］.一种解决的办法是通过硬件积分器得到角增量信号.在此基础上，有学者提出了基于角增量加角速率信号(称为硬件增强角速率)［4-7］的算法结构.另一种方法是采用基于纯角速率信号［8-9］的算法结构.从优化过程中的残留误差来看，这2 类算法具有同样优越的性能，但是鲜有文献对这些算法的姿态解算精度进行分析(特别是姿态解算的精度极限).此外，国外有学者提出了新的优化思路，采用最小二乘法使某一频率范围内的算法误差达到最小［10］.

本文推导了经典圆锥运动环境下旋转矢量变化量的真值，分析了传统的硬件增强角速率优化算法的姿态解算精度，阐述了算法中周期分量的影响;在此基础上，提出了一种改进的算法，对传统算法中的周期分量进行了二次优化;最后，利用Matlab进行仿真以验证理论分析和算法推导的正确性.

1 传统的硬件增强角速率圆锥算法

经典圆锥运动环境下，表征坐标系之间相对运动的姿态四元数q(t)和角速率ω(t)分别为

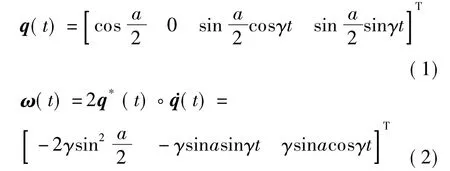
式中，a 为半锥角;γ=2πf，f 为锥运动频率［1］.

姿态四元数更新通常采用如下的迭代形式:

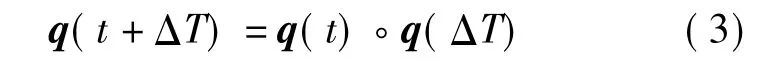
式中，q(t +ΔT)和q(t)分别为t +ΔT 和t 时刻的姿态四元数;q(ΔT)为时间间隔［t，t+ΔT］内姿态四元数的变化量，通常根据下式计算得到:

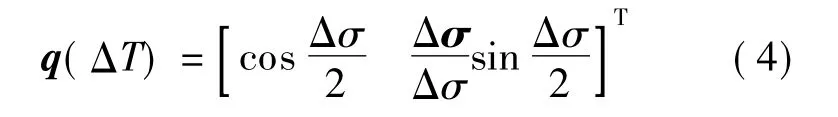
式中，Δσ=(Δσ·Δσ)1/2，Δσ 为时间间隔［t，t +ΔT］内旋转矢量的变化量［1］.

在传统的硬件增强角速率圆锥算法中，角增量和角速率信号构成了Δσ 的近似形式(记为Δ)，算法的优化目标就是在经典圆锥运动环境下根据Δσ 的理想值Δ最优地确定Δ中的一系列系数.Δ可以通过对Bortz 方程［2］积分并取前2 项近似得到.经典圆锥运动环境下，Δ可以表示为

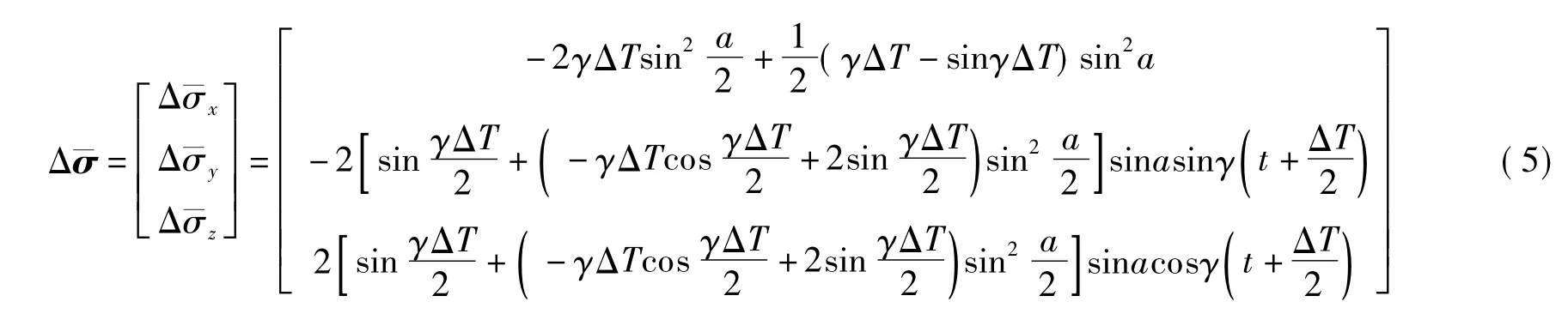
式中，仅x 轴分量不随时间变化，是非周期性的.

将时间间隔［t，t + ΔT］划分成N 个宽度为ΔT/N 的子区间，则可以在N +1 个时间点上从速率陀螺仪得到相应的角速率信号ωi(i =0，1，…，N).考虑到经典圆锥运动环境下所有矢量积ωi×ωj的非周期分量都只与(j－i)的值有关［4］，传统的硬件增强角速率圆锥算法通常表示为［4-7］

式中，ki为待优化的系数; α 为时间间隔［t，t +ΔT］内通过硬件积分器得到的角增量信号.

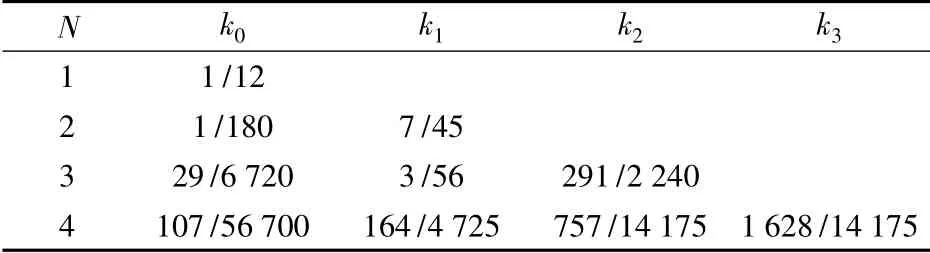
表1 传统的硬件增强角速率圆锥算法的优化系数

2 传统算法的姿态解算精度分析

传统的硬件增强角速率圆锥算法的优化只涉及非周期分量，如果满足γΔT ＜1 的条件，则子样数N 越大算法的残留误差越小［6-7］.考虑到上节中给出的参考基准是式(5)中的Δ，在只优化非周期分量的前提下，算法的姿态解算精度不可能通过增加子样数N 而无限地提高.具体的精度性能可以通过分析传统算法的各轴分量相对于Δσ 的真值以及Δ的误差进行确定.

经典圆锥运动环境下，姿态四元数的变化量q(ΔT)可推导如下［1］:

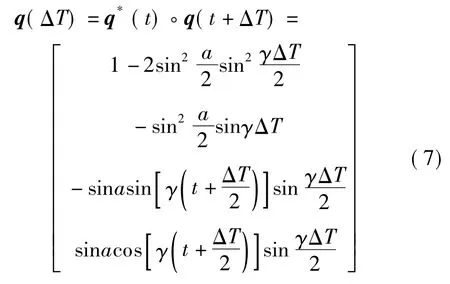
根据式(4)和(7)，可以确定Δσ 的真值，即

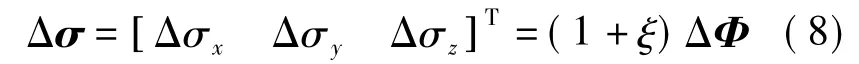
式中

式(10)表明，参数ξ 是关于半锥角a、锥运动频率f=γ/(2π)以及姿态四元数更新周期ΔT 的多元函数.

定义如下参数:

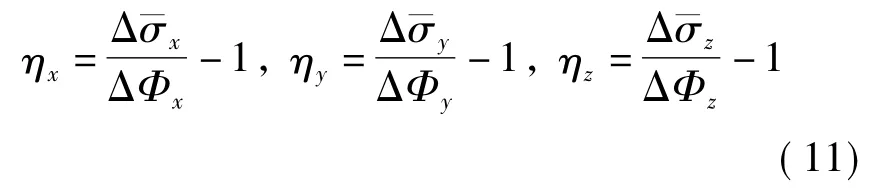
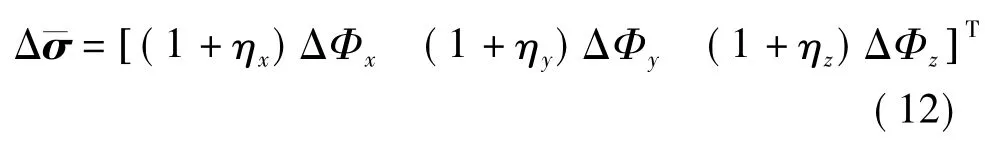
由式(8)和(12)可知，参数ηx，ηy，ηz与参数ξ之间的差距反映了Δ与Δσ 的真值之间的误差.

类似地，定义如下3 个参数:

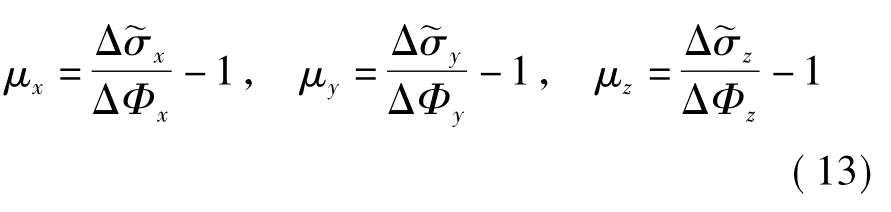
则式(6)所示的传统算法可以表示为

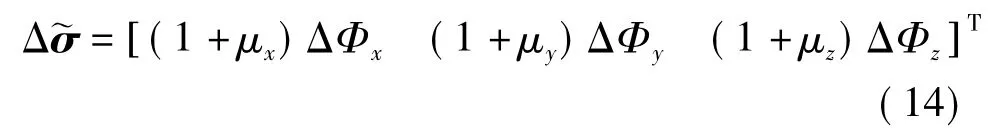
由式(8)和(14)可知，传统算法的各轴分量相对于Δσ 的真值的误差可以通过比较参数μx，μy，μz与参数ξ 进行确定.

由于式(12)和(14)结构相同，分别比较式(11)和(13)中的x，y，z 轴参数，即可确定传统算法的各轴分量相对于Δ的误差.

表2 表征理想值与真值之间误差的参数

表3 表征传统算法与真值之间误差的参数

由表2和表3可知，随着子样数N 的增加，参数μx逐渐逼近ηx，参数μy和μz不但偏离参数ηy和ηz而且表现出振幅越来越大的振荡.即当N =1时，传统算法与Δ之间的误差由x 轴分量决定;当N 达到3 时，传统算法与Δ之间的误差则由y轴和z 轴分量共同决定.此外，表3中的三子样和四子样算法在y 轴、z 轴方向的差距都不大.因此，可认为当子样数N 超过2 时，传统算法的姿态解算精度将不再提高.

3 改进的算法

考虑上节对姿态解算精度的分析，在传统硬件增强角速率圆锥优化算法的基础上，对算法中的周期分量进行二次优化.由于式(5)、(6)中y 轴和z轴分量的区别只是时变的正弦、余弦函数的不同，因此采用如下的系数矩阵替换式(6)中的待优化系数ki:

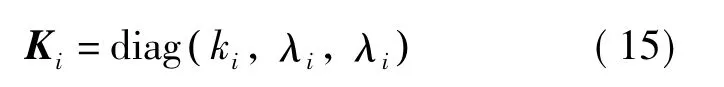
式中，λi为二次优化系数.

定义如下的二次优化误差准则:

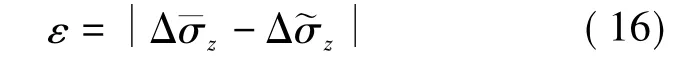
将式(5)和(6)的z 轴分量代入式(16)，可得

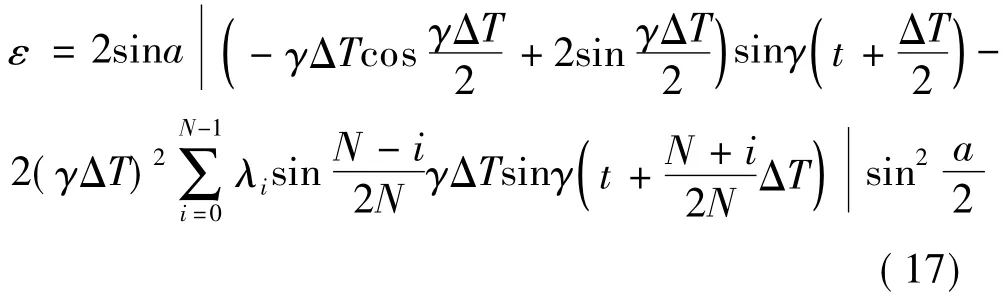
确定二次优化系数λi的步骤如下:

①将式(17)中的时变正弦函数统一展开成关于γ(t+ΔT/2)的三角函数;

②令关于γ(t +ΔT/2)的余弦项的系数之和为零，即

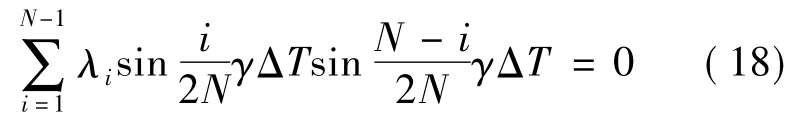
③将关于γ(t +ΔT/2)的正弦项的系数之和进行幂级数展开，然后令某些关于γΔT 的低阶项的系数为零，可得

④解式(18)和(19)构成的方程组，确定λi.

N=1～4 时的二次优化系数如表4所示，其中N=1 时的结果与表1中传统算法的优化系数相同.

表4 二次优化系数

4 仿真结果

在经典圆锥运动环境下，对传统算法和相应的改进算法的姿态解算精度进行仿真研究.表5为9 种经典圆锥运动的参数配置; 姿态四元数更新周期ΔT=0.01 s.仿真过程中，采用四阶幂级数截断形式［1］对式(4)中的三角函数系数进行近似.

图1～图4为8 号仿真环境下传统算法和相应改进算法的姿态解算精度.图1(a)为单子样算法的姿态解算精度，图1(b)为根据式(5)中的理想值Δ解算得到的姿态精度.限于篇幅，省略了与图1～图4类似的其他8 种仿真环境下的结果.

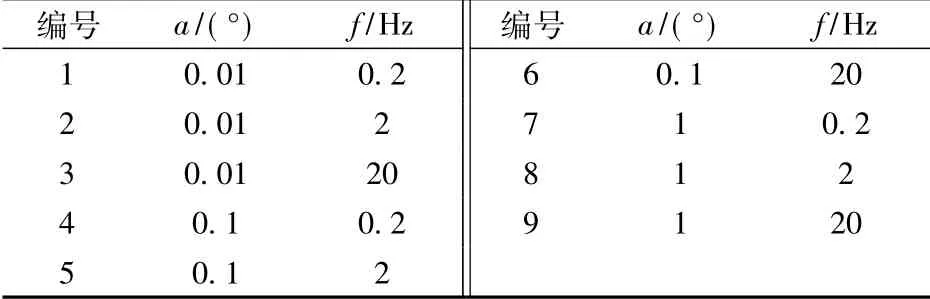
表5 经典圆锥运动参数配置

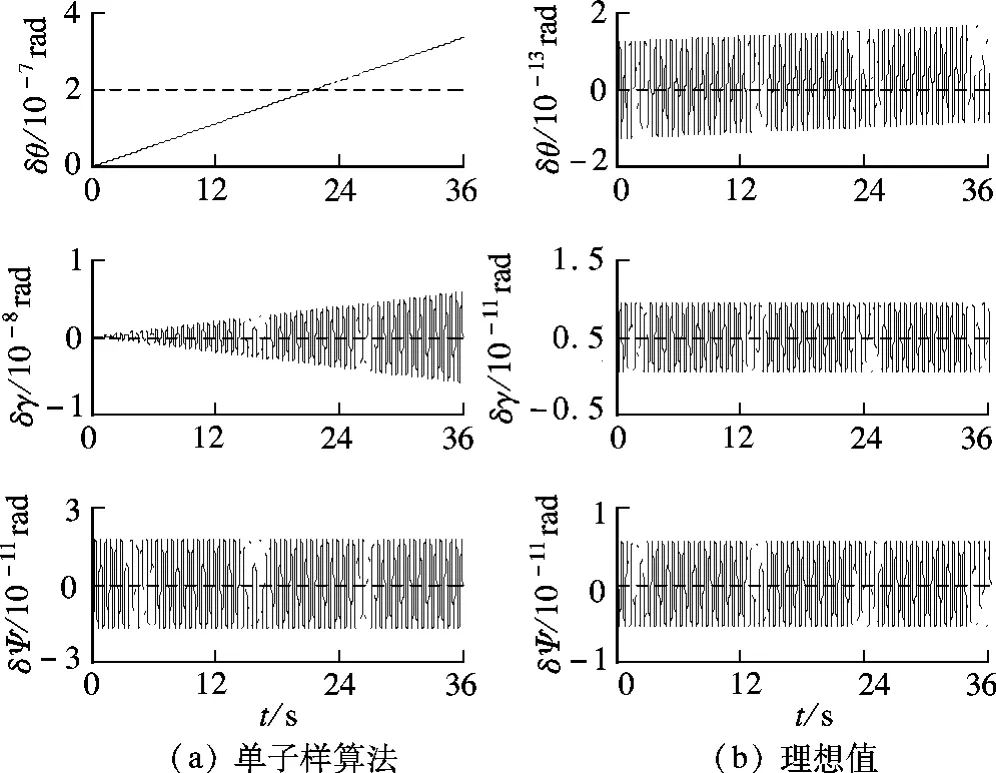
图1 单子样算法及理想值的姿态解算精度

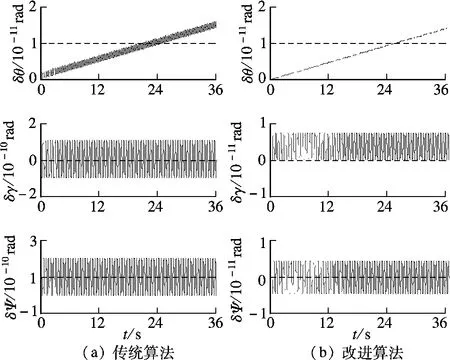
图2 N=2 时的姿态解算精度

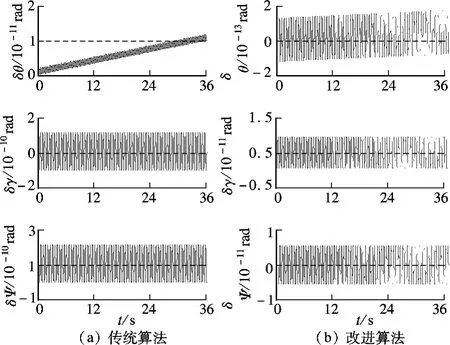
图3 N=3 时的姿态解算精度

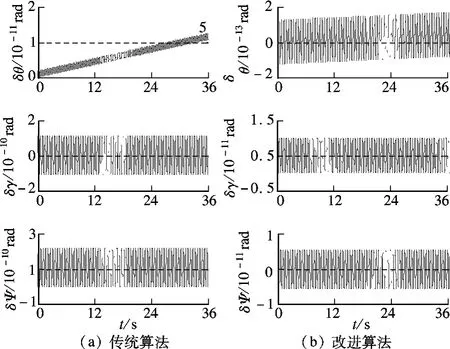
图4 N=4 时的姿态解算精度

图1～图4中，当子样数超过2 时，传统算法的姿态解算精度不再有明显的提高，这与第2 节的分析结果完全一致.子样数N =2 时，根据改进算法解算得到的横滚角误差(δγ)和航向角误差(δΨ)比传统算法减小了1 个数量级; 俯仰角误差(δθ)虽然没有减小，但是消除了原有的强烈振荡.这表明针对传统二子样算法中的周期分量进行的二次优化是有效的，而且改进的二子样算法的姿态解算精度主要由x 轴分量的残留误差决定.此外，改进的三子样和四子样算法的姿态解算精度与根据式(5)中的理想值Δ¯解算得到的结果几乎完全一致(见图1(b)、3(b)和4(b)).这是因为传统三子样和四子样算法中的x 轴分量本身就与理想值Δ很接近(见表2和表3).

式(6)中，由于矢量积运算的次数随子样数N的增加而增加，因此在考虑同样的精度性能时，改进的三子样算法更值得推荐.

5 结语

传统的硬件增强角速率圆锥算法的优化只涉及非周期分量.分析表明:在子样数超过2 时，传统优化算法中周期分量是主要的影响因素，相应的姿态解算精度不再提高.在此基础上，提出了一种改进的算法，对传统算法中的周期分量进行了二次优化.仿真结果表明对传统算法的姿态解算精度的分析是正确的，而且只需采用改进的三子样算法就可使最终的姿态解算精度与根据理想值得到的结果几乎完全一致.

References)

［1］Miller R B.A new strapdown attitude algorithm［J］.Journal of Guidance，Control，and Dynamics，1983，6(4): 287-291.

［2］Bortz J E.A new mathematical formulation for strapdown inertial navigation［J］.IEEE Transactions on Aerospace and Electronic Systems，1971，7(1): 61-66.

［3］黄昊，邓正隆.角速率输入下的航姿算法研究［J］.中国惯性技术学报，2000，8(2): 21-26.

Huang Hao，Deng Zhenglong.Study of navigation attitude algorithms for angular rate input［J］.Journal of Chinese Inertial Technology，2000，8(2): 21-26.(in Chinese)

［4］黄昊，邓正隆.旋转矢量航姿算法的一种新的表达式［J］.宇航学报，2001，22(3): 92-98.

Huang Hao，Deng Zhenglong.A new expression for rotation vector attitude algorithm［J］.Journal of Astronautics，2001，22(3): 92-98.(in Chinese)

［5］魏晓虹，张春熹，朱奎宝.一种高精度角速率圆锥补偿算法［J］.北京航空航天大学学报，2005，31(12):1312-1316.

Wei Xiaohong，Zhang Chunxi，Zhu Kuibao.High accuracy coning compensate algorithm by angular velocity［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31(12): 1312-1316.(in Chinese)

［6］曾庆化，刘建业，赵伟，等.激光陀螺惯导系统硬件增强角速率输入圆锥算法［J］.东南大学学报: 自然科学版，2006，36(5): 746-750.

Zeng Qinghua，Liu Jianye，Zhao Wei，et al.Coning algorithm with hardware-enhanced angle rate of RLG SINS［J］.Journal of Southeast University: Natural Science Edition，2006，36(5): 746-750.(in Chinese)

［7］Wei X Y，Fu Z X，Deng Z L.Research on coning compensation algorithms for SINS of angular rate input［J］.Journal of Harbin Institute of Technology:New Series，2007，14(4): 541-544.

［8］曾庆化，刘建业，熊智，等.一种角速率激光陀螺惯导系统高精度姿态算法［J］.上海交通大学学报，2006，40(12): 2159-2163.

Zeng Qinghua，Liu Jianye，Xiong Zhi，et al.A highaccuracy attitude algorithm of ring laser gyro strapdown inertial navigation system with pure angle rate output［J］.Journal of Shanghai Jiaotong University，2006，40(12): 2159-2163.(in Chinese)

［9］Ben Y Y，Sun F，Gao W，et al.Generalized method for improved coning algorithms using angular rate［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45(4): 1565-1572.

［10］Savage P G.Coning algorithm design by explicit frequency shaping［J］.Journal of Guidance，Control，and Dynamics，2010，33(4): 1123-1132.