煤粒中瓦斯时变扩散规律的解析研究

张志刚

（1.瓦斯灾害监控与应急技术国家重点实验室，重庆400037;2.中煤科工集团重庆研究院，重庆 400037）

煤粒中瓦斯时变扩散规律的解析研究

张志刚1，2

（1.瓦斯灾害监控与应急技术国家重点实验室，重庆400037;2.中煤科工集团重庆研究院，重庆 400037）

针对瓦斯在煤粒中的菲克型扩散，对煤粒瓦斯放散过程中扩散系数发生变化的机理进行了分析，并通过求取时变扩散系数Dt的公式对南桐煤样在瓦斯解吸放散过程中的扩散系数变化规律进行了测定，通过对实验数据的分析，得出了时变扩散系数的数学模型，推导出了时变扩散方程的解析解。

瓦斯;时变;扩散规律;扩散系数

瓦斯在煤层中的流动是孔隙中扩散和裂隙中渗流的综合过程。煤层中存在相互连通的裂隙网络，沿着这些裂隙网络，游离瓦斯流向低压工作面，而煤体的透气性系数与该裂隙网络密切相关。与此同时，块煤内部的瓦斯解吸向裂隙扩散，因此，煤层中瓦斯的渗透率和瓦斯的扩散性共同决定了瓦斯的流动状况。当瓦斯运移的孔隙直径很小，小于瓦斯分子的平均自由程，气体分子在孔隙中不能自由运动时，瓦斯的质量流将与瓦斯的浓度梯度成正比，符合扩散定律，即菲克定律［1－2］。

煤作为一种多孔介质，其瓦斯扩散系数在扩散的过程中是随着浓度不断变化的，与浓度依赖性很强，即呈现出时变性。而目前对许多菲克型扩散煤样的瓦斯解吸放散实验研究发现，即使瓦斯扩散系数D与浓度有关，而在煤粒解吸放散瓦斯的初始阶段，在t时间内的放散量Qt与t→∞时极限瓦斯放散量Q∞仍然具有关系Qt/Q∞=［3－4］，这说明时变扩散系数与扩散系数为常数的扩散过程具有相似的浓度变化规律。

本文针对菲克型扩散，对瓦斯放散过程中扩散系数的变化进行了分析，通过利用瓦斯放散曲线求取不同时间扩散系数Dt的公式，对煤粒解吸放散瓦斯过程中的扩散系数的变化规律进行了研究，得出时变扩散系数的数学模型，并结合菲克定律，推导出了时变扩散方程的解析解。研究煤粒中瓦斯时变扩散规律，对于煤与瓦斯突出危险性预测、煤层瓦斯含量预测及计算落煤瓦斯涌出量都具有很重要的实际意义。

1 瓦斯放散过程中扩散系数变化规律的分析

结合现代化学理论可知，分子的有效扩散系数与多孔介质的孔隙率和平均孔径算得的弯曲系数有关，即:

式中，Deff为有效扩散系数;D为扩散系数;φ为孔隙率;ζ为弯曲因数，对孔道弯曲造成的阻力所作的校正。

由 （1）式可知，瓦斯在煤粒中的有效扩散系数主要受孔隙率和弯曲因数的影响。煤吸附瓦斯将产生基质膨胀效应，我国学者已针对这一问题进行了大量的研究［5－6］，结果表明:煤吸附瓦斯而产生的变形将使得煤体孔隙率减小，同时吸附瓦斯还将改变煤粒中瓦斯扩散孔道弯曲系数，增加瓦斯气体分子在煤粒中扩散的阻力。反之，煤吸附瓦斯饱和后，在恒温恒压下放散瓦斯也会对瓦斯扩散阻力产生影响。因此，在煤粒瓦斯放散的过程中，扩散系数由于受到瓦斯浓度变化的影响而不断发生改变。正是由于瓦斯扩散系数的不断变化，从而使得实际扩散过程与理想模型Q=不一致。因此，把扩散系数作时间函数进行处理后，用菲克定律描述瓦斯在煤粒中的扩散过程更符合实际。

2 求取不同时间扩散系数Dt

结合以上分析，针对瓦斯放散过程中的时变扩散系数的扩散模型提出如下假设 （见图1）:

（1）煤粒为均质、各向同性球形颗粒。

（2）瓦斯在煤粒中的流动遵循质量守恒和连续性原理。

（3）变瓦斯扩散系数的扩散模型的解为扩散系数为常数时的解与时间函数Xt的乘积。

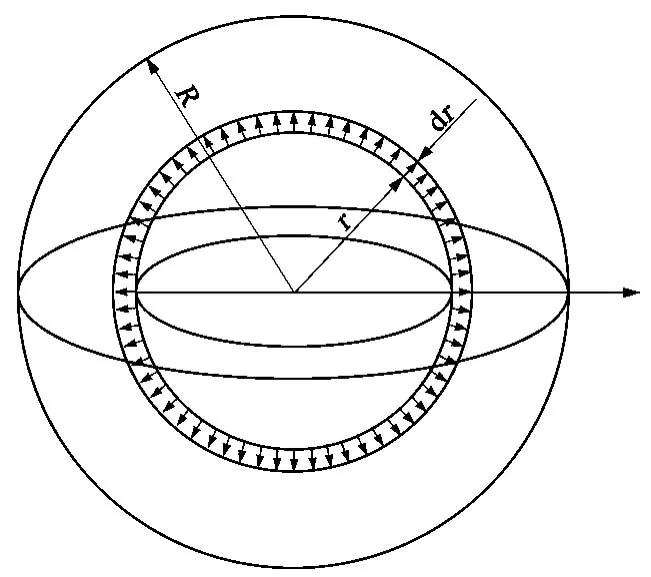
图1 煤粒瓦斯扩散

对于瓦斯扩散系数为常数时的扩散，其扩散方程和边界条件为［3］:

方程 （2）中，R为煤粒的半径;c（r，t）为煤粒径向上的浓度。

将方程 （2）的解做一定处理，可得:

（3）式中cat为时间t时半径R的煤粒内的平均浓度;c0和c1分别为初始时刻与煤粒表面的均匀浓度;Xt为时间函数，与浓度、时间、煤的吸附性能等有关;Dt为扩散时间t时或与浓度cat对应的扩散系数。

对于某一特定时间τ，当扩散时间t趋于τ时，根据煤样瓦斯解吸放散曲线的连续性，则有:

利用以上式子给出的直线关系，可以求出特定放散时间τ时的扩散系数Dτ，以及函数Xτ的数值。采用相同的方法，可以求出放散曲线上任一点所对应的扩散系数和待定函数X［4］。

3 实验验证

在关于煤的甲烷吸附量测定实验系统基础上，中煤科工集团重庆研究院自行研制了一套煤粒瓦斯解吸放散规律的实验装置。整套实验系统由真空脱气系统、瓦斯吸附—解吸放散系统和高压甲烷气瓶组成 （如图2），可对煤样解吸瓦斯曲线进行测定，记录对应时间下的煤样瓦斯解吸扩散量。

根据1节中的分析，利用瓦斯解吸放散实验装置对南桐矿务局鱼田堡煤样放散曲线进行了测定。通过汞密度法对煤样孔隙特征进行测定［7］，结果表明:所用煤样的诺森数Kn≥10，满足菲克扩散的条件。试验煤样粒度 0.2～0.25mm，重30.0003g。首先将煤样置入真空干燥箱，烘干24h，而后对煤样罐充入一定压力99.99%的甲烷，吸附48h后，记录平衡压力值，利用煤样的工业分析、吸附常数等参数，即可计算出实验煤样吸附瓦斯量，而后测定煤样瓦斯放散量及其对应时间，实验结果见图3。利用2节中的推导式即可求出不同时间煤粒瓦斯扩散系数Dt，计算结果见图4。

由图4可以得出:瓦斯扩散系数处于10－9数量级上，在放散初期和放散末期，瓦斯扩散系数基本趋于平缓，而在中期的某一时间段呈现出剧烈的增加。因此，直接套用以菲克定律为基础推导出的模型Q=来描述瓦斯在煤粒中的扩散过程存在一定的误差。通过对图4中实验数据的回归分析，发现Dt与时间较好地符合:

图2 煤粒解吸放散实验装置系统

图3 煤样瓦斯放散曲线

图4 扩散系数随时间的变化

实验煤粒孔径与瓦斯分子自由程相当，吸附平衡后煤样孔径变小，因而在放散的初期瓦斯分子在孔隙中的扩散阻力很大，随着煤粒中瓦斯浓度的降低，煤样孔径逐渐变大，但在放散的初期孔径改变的程度与瓦斯分子自由程相比仍然较小，因而在初期的一段时间对扩散系数的影响不大。随着瓦斯的逸出，孔径改变对瓦斯分子的扩散影响愈加明显，煤粒中瓦斯浓度降低使得扩散系数增大明显。在放散末期，煤粒孔径变化逐渐变小，其改变程度与瓦斯分子自由程的比值变化较小，因而这一时段的瓦斯扩散系数变化较小，可以认为是一常数。

4 基于时变扩散系数的球向扩散模型

5 结论

（1）由于煤与瓦斯气体分子间的吸附作用，使得煤粒瓦斯解吸扩散的过程中煤粒的孔隙率和弯曲因子随瓦斯浓度的变化而变化，进而使得扩散系数在整个放散过程中也随之而发生改变。

（2）利用求取时变扩散系数Dt的公式对诺森数Kn≥10的南桐煤样在不同放散时间的扩散系数进行了计算，结果表明:在放散初期和放散末期，瓦斯扩散系数基本趋于平缓，而在中期的某一时间段呈现出剧烈的增加。通过对实验数据的分析，发现扩散系数与时间的关系符合下式:

因此，把扩散系数作时间函数进行处理后，用菲克定律描述瓦斯在煤粒中的扩散过程更符合实际。

（3）通过对实验所得出的时变扩散系数的数

［1］聂百胜，何学秋，王恩元.瓦斯气体在煤层中的扩散机理及模式［J］.中国安全科学学报，2000，10（6）:24－28.

［2］聂百胜.煤粒瓦斯解吸扩散动力过程的实验研究［D］.太原:太原理工大学，1998.

［3］杨其銮，王佑安.煤屑瓦斯扩散理论及其应用［J］.煤炭学报，1986（3）:87－93.

［4］刘中民，郑禄彬，陈国权，等.与浓度相关的扩散系数Dt的求取 ［J］.中国科学 （B辑），1995，25（7）:704－709.

［5］王佑安，陶玉梅，王魁军，等.煤的吸附变形与吸附变形力［J］.煤矿安全，1993（6）.

［6］刘延保，曹树刚，李 勇，等.煤体吸附瓦斯膨胀变形效应的试验研究［J］.岩石力学与工程学报，2010，29（12）:2484－2491.

［7］陈瑞君，王东安.南桐矿区煤的微孔隙与瓦斯储存、运移关系［J］.煤田地质与勘探，1995，23（2）:29－31.

［8］严镇军.数学物理方程［M］.合肥:中国科学技术大学出版社，2004.

Resolving of Methane Time-varying Diffusion Rule in Coal Grain

ZHANG Zhi-gang1，2
（1．State Key Laboratory of Methane Disaster Monitoring＆ Emergency Technology，Chongqing 400037，China;
2．Chongqing Research Institute，China Coal Technology＆ Engineering Group，Chongqing 400037，China）

For Fick diffusion of methane in coal grain，diffusion coefficient variation mechanism was analyzed during methane emission and diffusion coefficient variation rule was tested during methane desorption and emission in coal sample from Nantong by solving time－varying diffusion coefficient equation．Mathematic model of time-varying diffusion coefficient was obtained and analytic solution of time－varying diffusion equation was deduced with test result．

methane;time varying;spread rule;diffusion coefficient

TD712.51

A

1006-6225（2012）02-0008-04

2011－12－26

国家科技重大专项大型油气田及煤层气开发:煤层气与煤炭协调开发关键技术 （2011ZX05040－003）

张志刚 （1978－），男，山西忻州人，高级工程师，长期从事煤层气开发及瓦斯治理工作。

［责任编辑:王兴库］

开采技术与装备