基于微遗传算法的多目标Box-Behnken设计试验条件优化分析*

山西医科大学公共卫生学院卫生统计学教研室(030001) 杨晓文 韩荣荣 徐彦杰 刘晓红 仇丽霞

在制药工艺中，研究有效药物成份与辅料的最佳剂量时，往往需要在达到有效的药物浓度的前提下，同时保证药物的副作用尽可能小，各类辅料的用量合理，这样就需要通过试验确定药物成份和辅料的最佳剂量，即寻找一组既满足约束条件又使总目标函数最优化的决策变量的取值，我们将其统称为多目标优化问题。在多因素、多水平的试验研究中，常常使用析因设计，当因素和水平数过多时，试验次数过多，使其不具备可行性，如三因素三水平析因设计需进行33次试验。Box-Behnken设计(BBD)是由Box和Behnken在上世纪60年代提出一种拟合二阶响应曲面的三水平设计，它是由2k析因设计与不完全区组设计组合而成，是一种多因素三水平的试验设计方法〔9〕。与析因设计相比，该设计可以明显减少试验次数，提高试验效率，降低试验的成本。微遗传算法(micro-genetic algorithm，micro-GA)，是近几年新发展起来的确定优化试验条件的优化方法之一，通过模拟自然进化过程，使原始数据在迭代过程中产生“遗传和变异”，并从全局的角度去寻找最优试验条件，相比较于传统的优化方法，如:看一看、算一算的直接法、最速上升法(下降法)、等高线图法等，可以有效避免最优试验条件选取时的主观性和局部最优解问题。

本研究旨在从统计分析的角度，利用模拟数据，对微遗传算法和传统优化方法确定的多目标最优试验条件的效果进行比较〔1－3〕。利用Matlab软件的函数模块、图形模块编制的遗传算法程序，为多因素三水平Box-Behnken设计的结果分析提供更为科学、高效的寻优方法。

原理及方法

1.Box-Behnken试验设计(BBD)

该设计是一种拟合响应曲面的二阶三水平设计，由2k析因设计与不完全区组设计组合而成，所得出的设计对所要求的试验次数来说十分有效，且它们是可旋转的或接近可旋转的。这种设计的另外一个优点就是它是球形设计(图1)。

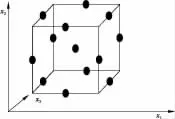
图1 Box-Behnken设计(k=3)

由图1可知BBD设计是一个球面设计，所有设计点都在半径为的球面上，即正方体各棱的中点，以及一个中心试验点。BBD设计不包含由各个变量的上限和下限所生成的立方体区域的顶点处的任一点。所以当立方体顶点所代表的因子水平组合因试验成本过于昂贵或因试验限制而不可行，此设计就显示出它特有的长处。图中每个设计点的三维立体坐标即代表了每一试验点的三个试验水平，试验本身要求三个水平在整个域里是平均分布的。

BBD设计试验次数N=2k·(k－1)+C0，公式中k表示因素的个数，C0表示中心试验点的重复次数，用于估计试验误差。

2.模型的建立

大多数最优化方法是从二阶函数模型导出的，实际上这种做法通常是有效的，主要是因为一般函数在极值点附近常可用二阶函数很好的进行近似。而且二次函数具有二次终止性，所谓二次终止性是指当算法应用于二次函数时，只要经过有限步迭代就能达到函数的极值点，具有很好的收敛性质。因此，利用Expert Design软件模拟影响因素和响应变量之间的非线性关系，建立二阶响应面方程，做为本次研究中遗传算法和传统优化方法搜索最优试验条件的目标函数。二阶响应面模型的一般表达式为:

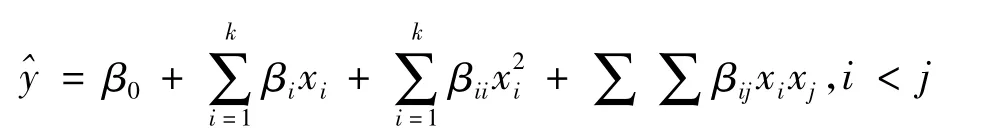
从模型中可以看出，二阶响应面模型分别考虑了影响因素的一阶主效应，二阶主效应，以及因素间的交互作用。对于响应值与因素之间呈现非线性的函数关系时，二阶响应面模型可以很好的去拟合它们之间的关系。

3.优化算法

(1)传统优化算法

①直接法

根据Box-Behnken试验设计及方差分析结果，在试验范围内选取“最优条件”，由于采用的试验设计具有最优设计的特性，若最佳控制点没有偏离试验范围，此法确定的最优试验条件一般比较理想。

②最速上升(或下降)法

最速上升法是以多项式响应面模型为基础，沿响应有最大增量的方向逐步移动，该方向平行于响应曲面等高线的法线方向，通常取感兴趣区域的中心且垂直于曲面等高线的直线为最速上升路径，直到观察到的响应不再增加为止。当然，如果求的是最小值，则叫最速下降法。

当然，若要同时考虑多个目标响应，即多目标问题时，确定“最优”试验条件应包括如下三个过程:首先，运用最速上升(或下降)法快速进入每一个响应(Yi)最优点试验区域;其次，在该实验区域内对每一个响应建立一个合适的响应曲面(二阶函数模型);最后，利用Expert Design软件包的满意度函数法，搜索最佳试验条件并优化所有响应，或至少使各响应保持在理想的范围内。

满意度函数法〔5〕(desirability function D)是由Derringer and Suich于1980年推广的同时优化技术。其方法是将各个响应Yi转换为单个满意度函数di，其变化范围是0≤di≤1，如果响应Yi是它的目标值，则di=1;如果响应在可接受的范围之外，则di=0。然后，选择设计变量，使之最大化m个响应的总满意度:D=(d1·d2…dm)1/m，并寻找各影响因素的最佳条件。

(2)微遗传算法

微遗传算法(micro-genetic algorithm，micro-GA)是一种基于小种群和再初始化的操作的特殊遗传算法〔6〕，是求解最优化问题的全局优化方法，适于优化处理复杂的多目标、非线性系统。

微遗传算法一般经过这样几个过程:①随机生成一个规模较小的种群，该种群形成一个种群内存，内存中分两种，一种可被置换，另一种不能置换。②以一定概率从两种内存中抽取形成初始种群。③选择得到Pareto非劣解，常规实施的遗传算子有:锦标赛选择、两点交叉、均匀变异、和精英主义〔7〕。④将选择得到的非劣解与外部内存集合比较，若仍保持非劣，则加入到种群内存中。⑤经给定代数的进化以后，把最好的非劣解作为优化问题的最优解。

利用Matlab2009a软件的函数模块、图形模块编制遗传算法程序，该程序经测试效果理想、程序可行、计算时间短〔8〕。采用二进制编码，随机种群=30，取初始种群(population)=6，其中可置换部分=2，进化代数(generation)=100，单点交叉概率(probabilitycrossover)PC=0.80，变异概率(probability-mutation)Pm=0.00，三目标优化运行次数为100次。

实例分析

1.资料

选用静脉注射克拉霉素(CLA)乳剂产生的血管刺激作用试验条件优化数据〔4〕，影响因素有:琥珀酸维生素 E(X1)、泊洛沙姆 －188(X2)、0.1 mol NaOH(X3)，试验中三个因素的取值范围分别是:琥珀酸维生素 E(%，W/W):30～76、泊洛沙姆 －188(%，W/V):0.5～1.5、0.1M NaOH(%，V/V):10 ～20。评价指标有:粒径(nm)(Y1)、ζ电位(mV)(Y2)、CLA 乳剂相分布率(%)(Y3)。在保证克拉霉素有效治疗浓度的前提下，为使药物对血管壁的刺激作用最小，评价指标在控制范围分别是:粒径(nm)达到最小、ζ电位(mV)达到最大、CLA乳剂相分布率(%)达到最大。

2.优化分析

(1)建立试验方案

根据试验因素和评价指标选取三因素三水平的Box-Behnken设计，因素数和水平数见表1。

在Box-Behnken试验设计给定的条件下，采用Expert Design软件建立试验设计方案，按实验次序进行试验。各因素试验条件已给出，所得的实际观察值分别是:粒径(nm)(Y1)、ζ电位(mV)(Y2)、CLA 乳剂相分布率(%)(Y3)，见表2。

表1 影响克拉霉素血管刺激作用的因素及水平

表2 三因素三水平BBD试验设计表及试验结果

Y Y Y变异来源1 2 3 SS v F P SS v F P.42 9 24.3 0.0013 X1 86.46 1 1.15 0.3318 38.59 1 13.10 0.0152 6.50 1 13.5 0.0144 X2 6.3 1 0.08 0.7834 7.45 1 2.53 0.1726 18.06 1 37.4 0.0017 X3 80.65 1 1.08 0.3470 90.25 1 30.64 0.0026 8.34 1 17.3 0.0088 X1X2 2265.76 1 30.2 0.0027 67.82 1 23.02 0.0049 9.03 1 18.7 0.0075 X1 X3 573.6 1 7.66 0.0395 55.35 1 18.79 0.0075 17.81 1 36.9 0.0017 X2X3 434.72 1 5.80 0.0609 10.99 1 3.73 0.1113 23.28 1 48.2 0.0009 SS v F P模型 4820.34 9 7.15 0.0216 341.46 9 12.88 0.0058 105 X21 379.14 1 5.06 0.0743 1.74 1 0.59 0.4767 0.33 1 0.7 0.4480 X22 363.1 1 4.85 0.0789 58.37 1 19.82 0.0067 21.18 1 43.9 0.0012 563.92 1 7.53 0.0406 6.40 1 2.17 0.2004 0.77 1 1.6 0.2614残差X23 374.58 5 14.73 5 2.41 5

(2)拟合二阶响应面方程及方差分析

利用Expert Design软件(Version 7.1.6.0)的方差分析对评价指标的试验数据(表2)进行分析，结果如下:

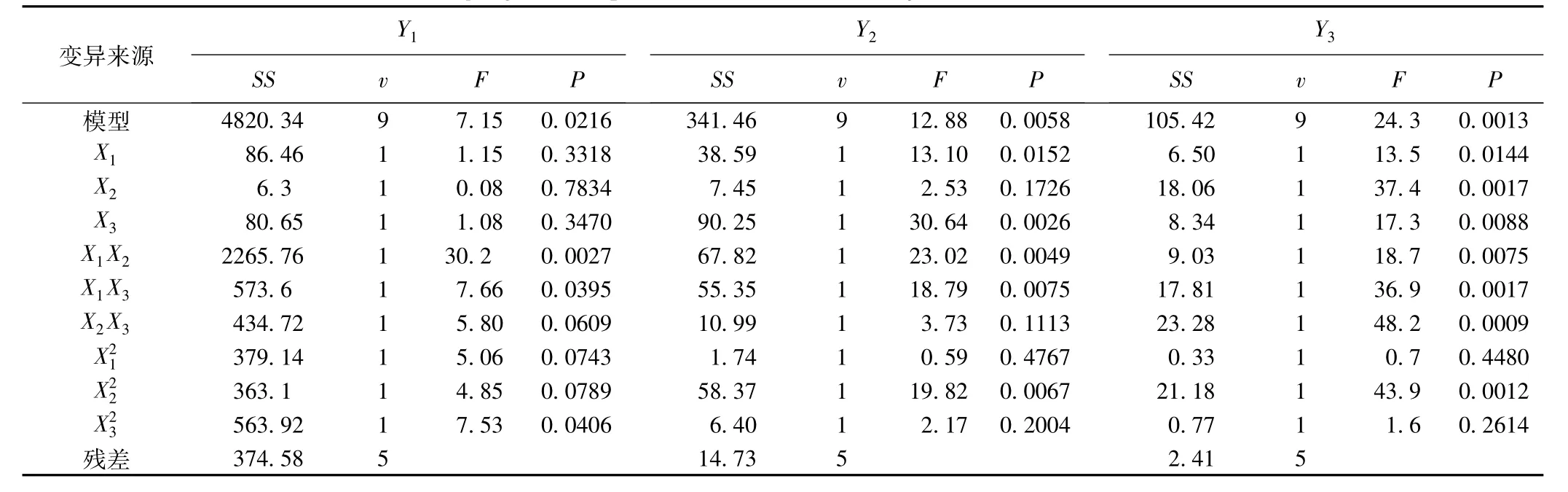
由表3知，经方差分析，三个模型的分析结果为:F1=7.15，P1=0.0216;F2=12.88，P2=0.0058;F3=24.3，P3=0.0013，按 α=0.05水准，模型拟合较好。Expert Design软件给出了三个二阶响应面全模型及决定系数(R2)如下:

表3 粒径(Y1)、ζ电位(Y2)、CLA乳剂相分布率(Y3)二阶响应面模型的方差分析

从表3中我们还可以看出，虽然泊洛沙姆－188(X2)的一阶主效应在三个模型中均无统计学意义，但其二阶主效应以及和其他因素的交互作用对模型的贡献均十分显著，这是因为X2对模型的贡献主要体现在其交互作用以及二阶主效应上，其中也包含了X2的一阶主效应对模型的贡献，同时结合专业知识我们得知，泊洛沙姆－188(X2)在加入到乳剂系统中时，会被其他原料部分替代。因此经统计学和专业知识综合分析后，在各因素交互作用显著的情况下，我们保留了模型中各因素的主效应。

(3)最优试验条件搜索

①经传统优化方法搜索

直接法 由表2中每一因素各水平试验条件下确定的“最佳”试验条件为:琥珀酸维生素E(X1)浓度76%、泊洛沙姆－188(X2)浓度0.5%、0.1 mol NaOH(X3)15%;此时的评价指标Y1=138.4 nm、Y2=30.72 mV、Y3=97.53%。

最速上升(或下降)法 如本例中含有粒径(Y1)、ζ电位(Y2)、CLA乳剂相分布率(Y3)，三个响应值，利用Expert Design软件包的满意度函数法，控制评价指标，使得粒径(Y1)达到最小、ζ电位(Y2)达到最大、CLA乳剂相分布率(Y3)达到最大的条件下，寻找试验因素的最优组合。所得的最佳试验条件及评价指标的预测值见表4。

②经微遗传算法搜索

表5为经微遗传算法(micro-GA)搜索的部分非劣解方案，按照研究目的为使得评价指标粒径(Y1)最小、ζ电位(Y2)最大、CLA乳剂相分布率(Y3)最大经

综合考虑，可选取比较理想的2号方案作为最优条件。即琥珀酸维生素E、泊洛沙姆－188、0.1M NaOH最佳条件分别为:68.25%、0.52%、15.26%，评价指标粒径、ζ电位、CLA乳剂相分布率分别为:135.75 nm、33.67 mV、98.12%。

表4 经满意度函数法确定各试验因素及评价指标最优条件

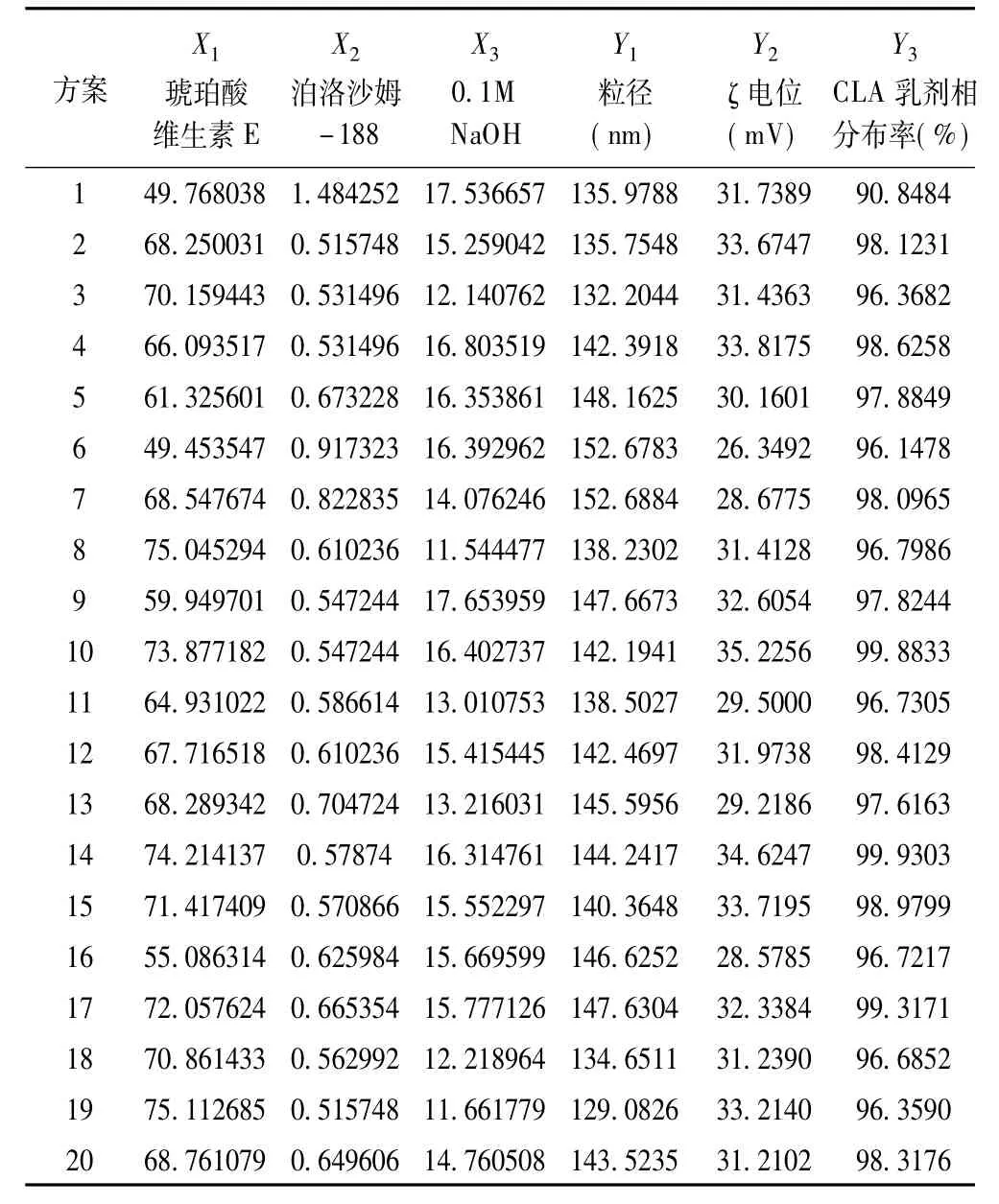
表5 三目标micro-GA非劣解方案

由表6可知，从20种方案的平均水平来看，载药率的精度较高，各试验因素的中位数基本在试验区域的平均水平;四分位数间距(IR)较小，精度较好;95%的置信区间基本囊括了各影响因素的试验范围，由此可知micro-GA的搜索从全局出发，搜索结果是理想的。

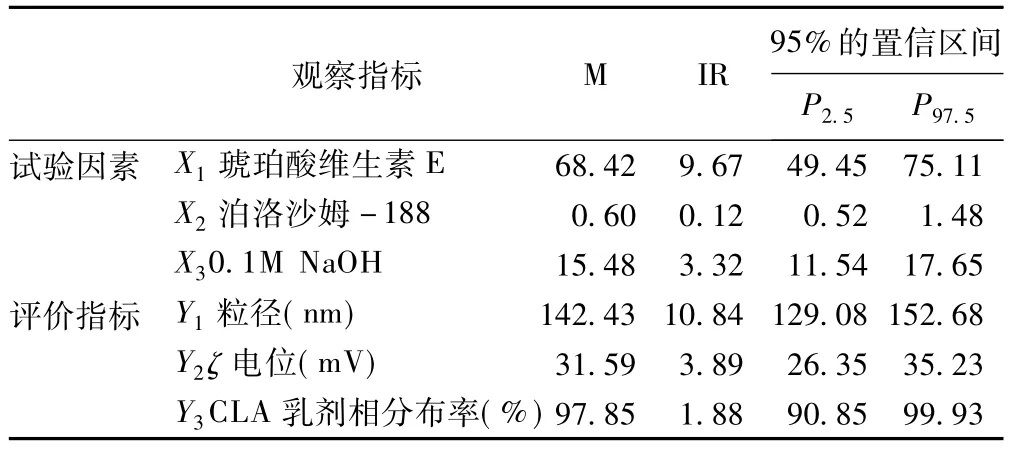
表6 三目标micro-GA非劣解方案平均水平

优化效果比较

对于本次模拟数据的结果，从微遗传算法的角度来看，评价指标粒径与满意度函数法搜索的最优值基本一致，ζ电位增加了2.43 mV，提高了8.47%，CLA乳剂相分布率增加了0.8%，因而确定的试验条件更为理想。而直接法只能在各试验水平上确定最优试验条件，不能预测评价指标的值。

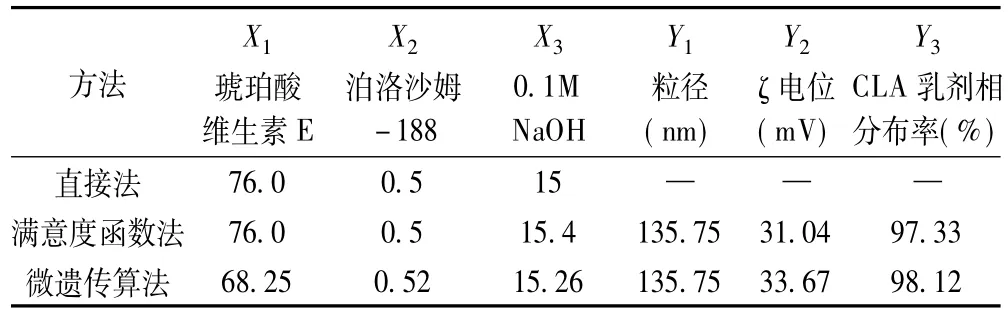
表7 三种寻优结果的比较

讨 论

Box-Behnken设计是一种基于三水平的二阶试验设计法，可以评价指标和因素间的非线性关系，尤其是各因素之间的交互作用。试验次数少，试验效果理想。但却要求每个试验因素的水平在各个试验区域中均匀分布。

微遗传算法和满意度函数法均利用二阶函数模型搜索最优试验条件，并对响应变量进行预测。从优化方法原理上来看，满意度函数法是将各个相应指标(Yi)转换为单个满意度函数(di)，然后用加权的方法将di置于总满意度函数(D)中，通过改变各个di的权重来使得总体满意度函数(D)最优，搜索范围固定，容易产生局部最优;微遗传算法是从单目标进化算法中发展而来，其要求的种群数量少，收敛效率高，可以从试验域中快速产生非劣解前沿，避免局部最优的问题。从优化效果来看，由微遗传算法搜索的试验条件明显优于满意度函数法，这充分体现了微遗传算法的全局搜索能力的优势。

微遗传算法对因素的取值可以是连续的，也可以是离散的。而基于最速上升(或下降)法的多响应变量优化的满意度函数法要求因素的取值必须是连续的，若是离散的，只能以连续性变量对待，对最后的搜索水平作近似估计。

1．崔逊学．多目标进化算法及应用．北京:国防工业出版社，2006．

2．仇丽霞．基于遗传算法的最优决策值选择及医药学应用研究．山西医科大学博士论文，2007．

3．王小平，曹立明．遗传算法的基本理论与应用．北京:科学出版社，2002．

4．Li J，Nie S，Yang X，et al．Optimization of tocol emulsions for the intravenous delivery of clarithromycin．International Journal of Pharmaceutics，2008，365:282-290．

5．G．Derringer，R．Suich，J．Qual．Technol，1980，12:214．

6．C．Coello G．Pulido，A micro-genetic algorithm for multi-objective optimization，Lecture Notes in Computer Science，1993(2001):126-140．

7．Leszek Siwik，Marek kisiel-dorohinicki elitism in agent-based evolutionary multi-objective optimition．Inteligencia Artificial，Revista iberoamericana de inteligencia artificial，2005，28(9):41-48．

8．李飞莹．基于微遗传算法的多目标药物提取条件优化分析．山西医科大学硕士论文，2010．

9．胡雅琴，何桢．响应曲面二阶设计方法比较研究．天津大学，2005．