倾向指数分层法的模拟研究*

潍坊医学院公共卫生学院(261053) 孟维静 王素珍 吕军城 石福艳

随机对照试验(RCT)被认为是临床试验研究最理想的金标准。但受一些研究条件及伦理学因素的限制，随机化受到很大限制〔1－2〕。当随机化不能够实现或者遭到破坏时，治疗效果的判断变得非常复杂，因为我们无法判定组间的差异是由于治疗或暴露所引起的，还是由于组间的分配不平衡而造成的。多元模型和倾向指数等方法是解决该问题的常用研究方法〔3〕。而且倾向指数方法易于理解、研究步骤标准化程度高，近年来应用倾向指数处理非随机化数据得到了更多的关注，有越来越多的研究者开始应用此方法来平衡组间的不均衡〔4〕。本文应用SAS程序模拟研究倾向指数分层法处理非随机化试验数据的效果。

原理与方法

倾向指数法是均衡组间偏倚的有效方法，由Rosenbaum 和Rubin在1983年首次提出〔5〕，其主要目的是通过均衡组间各个混杂因素变量来降低偏倚，其实质是将多个协变量的影响因素用一个倾向指数来表示(相当于降低了协变量的维度)，根据倾向指数进行不同治疗组间的匹配，对观测性数据的混杂因素进行类似随机化的均衡处理。倾向指数的具体定义是:按照给定的一组特征变量(xm)将任意一个研究对象i(i=1，2，…，N)划分到治疗组(Zi=1)的条件概率，第i个研究对象被分配到治疗组的概率可以表达为:e(xi)，即P，被称为倾向指数。

假设从治疗组选出研究对象i，则e(X)=pri(Z=1|X=xi)，再从对照组选出一个研究对象j，那么e(X)=prj(Z=1|X=xj);如果 Pri=Prj，则必然有xi=xj，如果尽量使Pri无限地接近Prj，则 xi和 xj必然十分接近〔6〕。因此，经过倾向指数调整的组间个体，除了处理因素和结果变量分布不同外，其他协变量应当均衡可比，相当于“事后随机化”，使观察性数据达到“接近随机分配数据”的效果。应用较多的倾向指数方法包括匹配(matching)、分层(stratification)和回归校正(regression adjustment)等〔7－8〕。

倾向指数分层法是把倾向指数作为分层的唯一标准，通过模型估计倾向指数后，按倾向指数进行分层，层内组间协变量应该是均衡的，将各层处理效应赋予权重后相加起来估计处理效应，并检查各层内暴露组和对照组间每个协变量的均衡性〔9〕。

在新药临床试验以及流行病学研究中，一般可以运用logistic回归方法来估计倾向指数，数学模型如下:

其中，e(xi)为倾向指数，α，β为模型的参数，其中α即组间效应，β为回归系数，X为协变量。

模拟设计

1．SAS生成数据过程

在上述假定的基础上，模拟生成A、B两组随访数据。由线性模型Y=Zδ+X'β+ε生成模拟数据，其中δ代表组间效应。首先生成协变量X，假定模型中有三个自变量:连续型变量X1，二分类变量X2，X3。为了模拟两组中协变量的不同分布情况，分别对处理组A和对照组B生成不同的协变量:对于处理组A(Z=1)，假定 X1～N(d，σ21)，X2～Bernoulli(p2t)和 X3～Bernoulli(p3t);对于对照组 B(Z=0)，假定 X1～N(0.2)，X2～Bernoulli(p2c)和 X3～Bernoulli(p3c)。通过控制 d和二项分布的概率 p2c，p2t，p3c和 p3t，可以模拟各种不同水平的协变量分布的情况。然后根据协变量X和处理分配Z，使用预先设定的δ、β和独立产生的正态分布误差ε～N(0，σ2ε)生长Y变量。根据上述模型和设定的参数值，由SAS模拟产生带有协变量的两组随机数，设定协变量的系数(β1，β2，β3)=(0.5，0.4，0.4)。其他参数值的设定为(σ1，δ，d，p2c，p3c，p2t，p3t，σε)=(0.6，0.1，0.5，0.3，0.7，0.5，0.9，1.0)。

用分组变量作因变量，协变量X1，X2，X3做自变量，建立logistic回归模型，并计算倾向指数，根据倾向指数进行五等分。分层前后分别对两组进行比较，对处理效应做出评价。同时，对分层前后协变量的均衡性进行比较，进而得出最终结论。在既定的参数设置下，程序每循环一次对一个总样本量为1000的两组数据完成一次模拟，SAS程序循环1000次后，模拟完成。

2．模拟结果

(1)处理效应的估计

分层之前，对于A、B两组间的处理效应，每次模拟的数据采用两样本t检验，循环1000次，1000次均有P＜0.05，无P＞0.05的情况出现，总体上表明两组间差异有统计学意义。

处理效应^δ的方差估计值可以用下面的公式计算〔10〕:

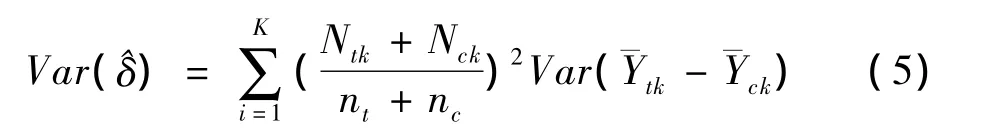
样本量较大时，^δ服从正态分布〔10〕，以此来估计处理效应。因此，五分层之后，对于A、B两组间的处理效应，用公式(6)进行统计推断。

对既定的样本，循环1000次，其中有948次P＜0.05，有52次P＞0.05，表明在平衡了协变量之间的不均衡后，两组间差异有统计学意义。

(2)协变量的均衡性比较

本文采用假设检验评价分层前后层内协变量的均衡性。循环1000次后，结果见表1。

表1 分层之前两组间协变量的均衡性

由表1可以看出，分层之前，对X1进行两样本t检验，循环1000次，1000次均为 P＜0.05，表明变量X1两组间差异有统计学意义。对于变量X2，X3采用四格表χ2检验，循环1000次，其中P＜0.05的次数均为1000次，总体上表明变量X2，X3在两组间均差异有统计学意义。说明变量 X1，X2，X3，在两组间都不均衡。

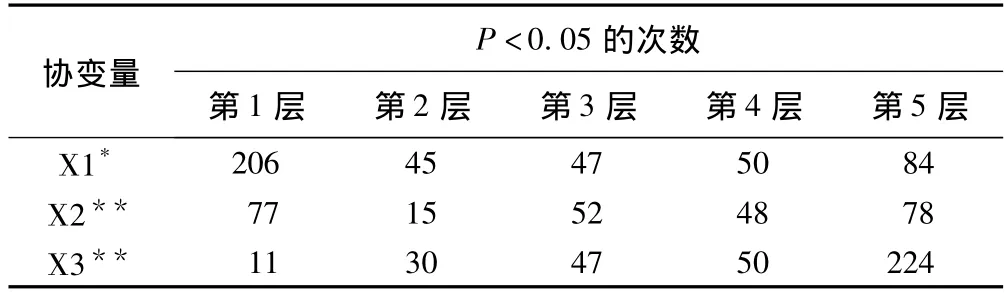
表2 分层之后层内两组间协变量的均衡性

分层之后，分别对X1，X2，X3层内进行检验，循环1000次，P＜0.05的次数如表2，除第1层和第5层，由于两组间的样本含量太小而导致I型错误的概率大于0.05外，其余的2、3、4层 P＜0.05的次数均小于5%，说明2、3、4 层中两组中 X1，X2，X3之间的差别均无统计学意义。表明变量X1，X2，X3在层内两组间基本达到了平衡。

讨 论

在随机化无法实现的试验研究中，倾向指数能很好地平衡协变量引起的组间不均衡性〔6〕。分层法是倾向指数应用较多的方法之一，Rosenbaum和 Rubin认为按倾向指数分为5层就能减少90%的偏倚〔11〕。而且倾向指数分层法简单易行，在大样本量的情况下，不会损失样本信息，因此得到广泛的应用。

虽然倾向指数分层法越来越多的被人们应用，但是它也有一定的局限性:(1)倾向指数分层法只能平衡可观测的变量，对于潜在的混杂因素无能为力〔12〕。(2)倾向指数分层法对大样本数据平衡能力较好，对小样本数据，很难达到满意的均衡效果。因为较少的样本量会导致某些特殊的情况出现，分层后组间协变量在最高层和最低层可能是不平衡的。(3)分层法协变量的均衡性只能在层内比较，不能直接比较研究样本的均衡性。因此，要注意考虑倾向指数分层法的应用范围。

本模拟研究结果表明，倾向指数分层法是一种很好的处理非随机化数据的方法，为以后非随机化临床试验数据的处理提供了理论基础。

1．Guo SY，Barth RD，Gibbons C．Propensity score matching strategies for evaluating substance abuse services for child welfare clients．Children and Youth Services Review，2006，28(4):357-383．

2．Concato J，Shah N，Horwitz RI．Randomized，controlled trials，observational studies，and the hierarchy of research designs．N Engl J Med，2000，342(25):1887-1892．

3．王永吉，蔡宏伟，夏结来，等．倾向指数的基本概念和研究步骤(第一讲)．中华流行病学杂志，2010，31(3):99-100．

4．Stürmer T，Joshi M，Glynn RJ，et al．A review of the application of propensity score methods yielded increasing use，advantages in specific settings，but not substantially different estimates compared with conventional multivariable methods．Journal of Clinical Epidemiology，2006，59(5):437-447．

5．Rosenbaum PR，Rubin DB．The central role of the propensity score in observational studies for causal effects．Biometrika，1983，70(1):41-55．

6．郑亮，夏结来，王素珍，等．非随机化临床试验中倾向指数的应用．现代预防医学，2009，36(15):2805-2809．

7．Hullsiek KH，Louis TA．Propensity score modeling strategies for the causal analysis of observational data．Biostatistics，2002，3(2):179-193．

8．Austin PC，Mamdani MM．A comparison of propensity score methods:a case-study estimating the effectiveness of post-AM statin use．Stat Med，2006，25(30):2084-2106．

9．王永吉，蔡宏伟，夏结来，等．倾向指数常用研究方法(第二讲)．中华流行病学杂志，2010，31(5):104-105．

10．Tu WZ，Zhou XH．A bootstrap confidence interval procedure for the treatment effect using propensity score subclassification．Health Services and Outcomes Research Methodology，2002，3(2):135-147．

11．Rosenbaum PR，Rubin DB．Reducing bias in observational studies using subclassification on the propensity score．Journal of the American Statistical Association，1984，79(387):16-524．

12．Brookhart MA，Schneeweiss S，Rothman KJ，et al．Variable selection for propensity score models．Prac Epidemiol，2006，163(12):1149-1156．