一种基于MOGA的含DG配电网络多目标重构方案

黄 烨

（1.华北电力大学电气与电子工程学院 2.杭州市电力局）

1 引言

配电网重构是在满足系统约束的条件下，通过改变分段开关和联络开关的开/合状态，寻找符合某特定运行要求的拓扑结构。它是配电系统运行和控制的手段，也是配电网管理系统（Distribution Management System，DMS）的重要内容。现阶段常用的算法有启发式算法[1]和随机优化方法[2~4]等。

近年来，随着大量分布式电源（Distribution Generation，DG）接入配电网，对节点电压、网络损耗、配电可靠性等方面产生了影响，给配电网重构带来了新的挑战，有专家学者对此做了一些工作[5~8]。文献[5]介绍了DG的接入对配电网重构的影响，同时采用改进遗传算法对含DG的配电网重构问题进行求解；文献[6]在Bender’s分解技术的基础上，将含DG配电网络重构分解为DG给定时确定孤岛系统最优供电容量和孤岛给定时降低系统网损的两部分优化过程，实现整个网络重构方案的优化；文献[7]针对含风力发电的配电网系统建立风力发电机和负荷随机模型，并采用粒子群引导的最小生成树算法进行计及风力发电随机性的配电网重构；文献[8]建立了计及风电出力随机性影响的配电网重构场景模型，并使用遗传算法进行求解。

以上研究中，均以降低网损作为配电网重构的主要目标。考虑到电力市场的强大需求，配电网可靠性是直接影响供电服务质量的重要因素，另外一些研究中，将提高可靠性纳入配电网络重构的过程中，成为优化目标之一[9~11]。文献[9]将区间分析应用于提高配电系统可靠性的措施中，提出了以提高系统可靠性为目标的配电网络重构的区间方法；文献[10]以某一时刻的网损和供电不可靠率（Average Service Unavailability Index，ASUI）的加权和为优化目标，采用遗传算法进行配电网络的重构；文献[11]对年期望电量不足和年网损总值进行加权建立妥协模型，将多目标优化转换为单目标优化。文献[10]、[11]的不足之处在于：所采用的可靠性和网损指标不能较好地表征工程实际中配电网的状态，如文献[10]中的 ASUI指标，只能表示系统中用户的断电概率，没有体现用户负荷等与经济损失直接挂钩的可靠性指标；文献[11]中，年网损总值由峰值负荷状态下的网损乘以年最大损耗小时数得出，误差较大；除此之外，可靠性和网损这两类指标的单位经济损失较难统一，两文中采用定系数的加权方法较为草率。

为了准确全面地评估含DG配电网络的状态，选取合适的指标较为重要。考虑到系统负荷和DG状态不断变化，在较长的时间跨度上评估配电网络状态，准确性较低。对于配电网而言，正常供电时，主要考虑经济运行的能力；故障时，故障负荷的大小和持续时间成为主要着眼点——不同状况下，两者的权重不同，较难定系数量化。

基于上述，本文取某一个较短的时间区间，视用户负荷和DG运行状态恒定不变，考虑DG的影响，将该时间段内的期望电量不足（Expected Energy not Supplied，EENS）作为系统安全供电能力的指标，稳态瞬时网损作为系统稳态经济运行能力的指标，构成多目标优化的两个目标；引入Pareto最优概念，提出了一种基于多目标遗传算法（Multi-Objective Genetic Algorithm，MOGA）的含DG配电网络多目标重构方案，综合物理意义和单位上无法统一度量的两类指标，能得到覆盖所有权重的Pareto最优解集。

2 数学模型

在含DG的配电网络中，故障前，网络结构为放射状，DG功率注入提高节点电压，降低系统网损；故障后，DG与部分线路、节点形成孤岛，向部分负荷继续供电。本文假设在此期间DG运行状态恒定。

如引言中述及，目标函数可表示如下：

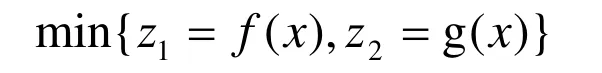
其中，z1= f(x)代表评估时间段内的EENS值，包括此时间段之前和此时间段内的故障导致的EENS值；z2= g (x)表示评估时间段内的稳态瞬时网损值。

需要满足的约束有：流量守恒约束、线路容量约束、电压约束、DG注入功率约束等。

3 MOGA简介

遗传算法（Genetic Algorithm，GA）将待求问题的解映射为单一种群中的个体，模拟自然界中“物竞天择，适者生存”的选择机制，通过种群的进化完成解的优化。在GA的基础上，引入多目标优化方法中Pareto最优的思想，形成了MOGA。较GA而言，改进之处主要有以下两点：

(1) 适应度评价

在GA中，个体的适应度一般通过目标函数值来确定。在MOGA中，多个目标无法统一度量，确定适应度值的方法如下所示：

假设两解S1及S2对所有目标而言，S1均优于S2，称S1支配S2；若S1没有被种群中其它解所支配，则S1称为非支配解，也称Pareto最优解。

按照上述定义对所有解个体进行分级，满足两个条件：① 同一等级的解互不支配；② 对于任一低等级解，在每个较高等级中，必定能找到一个或多个支配它的解个体。根据解个体所处等级，按照线性或非线性插值方法给不同等级个体赋以不同适应度值，同一等级的解个体共享适应度值。

(2) Pareto最优解集

建立一个Pareto最优解集，每一代均进行更新，保证其中的解不被当前或以前代的任何解所支配。运行至最大代数时，Pareto最优解集中的解个体即为所求的Pareto最优解。

4 重构方案

本文考虑 DG对配电网络的EENS值和网损值的影响，提出了一种基于 MOGA的含DG配电网络多目标重构方案，流程如图1所示。

图1 基于MOGA的含DG配电网络多目标重构方案流程图

4.1 编码方式和种群初始化

本文不考虑辐射状支路（应始终闭合），对其余支路采用二进制编码方式，1代表闭合、0代表断开，个体的染色体为一串二进制码，长度等于非辐射状支路的总数。

为了保证初始种群的可行性，本文提出一种“随机避环法”，生成初始可行个体：将所有非辐射状支路随机排列，并依次处理——若该支路的两端点不处于同一节点集中，将该支路状态置1，并将两端点所在节点集合并，表征连接关系；否则将该支路状态置0，避免产生环网。

依次操作产生整个可行初始种群。由于每个个体都是随机生成，初始种群保持了较好的多样性。

4.2 EENS及网损值计算

对于EENS值计算，本文做了如下假设：

(1) 故障率在全年范围内均匀分布；

(2) 两个故障同时发生的概率为0。

前已述及，EENS包括评估时间段前、段内故障造成的电量不足。假设评估的时间段为[T1~T2]，可能的故障有n类，从故障发生到转供所需的时间分别为= 1 ,2,...,n)，每类故障导致的功率不足（Power not Supplied，PNS）为 pi。令 Ti0=T2-ti，就第 i类故障而言，需考虑的时间段内为[Ti0~T2]。可得EENS的计算公式为 ，其中ci为第i类故障率，满足，λ为第i类i故障的全年发生次数；)表示每次故障时，评估时间段内的故障持续时间。

下面介绍ip的计算步骤：

(1) 首先计算无DG情况下的 pi值，用表示：=p， p为第i类故障所形成的孤岛中节点 sumsum总负荷；

计算网损时，将DG注入功率看作负的负荷，采用前推回代法进行潮流计算。

4.3 Pareto最优操作

本文中，Pareto最优操作的同时考虑优化问题的两个目标，保留当前的Pareto最优解。具体步骤为：对于当前种群中每一个个体，将其与Pareto最优解集中的个体进行对比，若其不被Pareto最优解集中任何个体所支配或与之相同，将其加入Pareto最优解集；否则无操作。操作完成后，Pareto最优解集中个体即为当前的Pareto最优解。

若Pareto最优解集的规模M超过了本身容量N，采用基于拥挤距离的剔除操作——将Pareto最优解集中的个体分布在EENS值和网损值所形成的平面坐标系中，对于每一个个体，计算临近的两个个体所构成的长方形的平均边长，即为该个体的拥挤距离。根据拥挤距离的大小对 Pareto最优解集中的个体进行排序，剔除序列最后一个个体，M=M－1。若M≤N，剔除操作完成；否则，重新计算个体的拥挤距离并排序，重复操作直至M≤N，剔除操作完成。基于拥挤距离的剔除操作能在控制 Pareto最优解集规模的同时，保证个体均匀分布。这样无论EENS值与网损值之间重要性如何，都能得到较为满意的结果。

4.4 精英回代操作

为了充分发挥Pareto最优解集的引导作用，同时有效地保持种群的多样性，本文采用了一种基于共享机制的精英回代操作——首先计算当前种群中各个体与其它个体的海明距离（Hamming Distance）之和，即染色体中不同基因的个数，并从大到小进行排序；剔除序列中排在后20%的个体，从Pareto最优解集中随机抽取同样多的个体填补。

4.5 适应度评价

进行适应度评价，首先需要根据个体的水平将种群分级。具体实现方法为：搜索当前种群，将所有的非支配解划分为同一级，并赋予相同的等级为1；然后剔除这些个体，在剩余个体中找出当前的非支配解，并赋予相同的等级为2；重复上述过程，直到种群中所有个体均被赋予相应等级为止。值得一提的是，由于这一代种群与Pareto最优解集并不完全相同，因此种群中部分等级为1的个体可能被Pareto最优解集中个体所支配。

本文在Pareto分级的基础上，对同一级个体赋予基于拥挤距离的虚拟适应度，操作与4.3节中方法类似，第i级中排序为j的个体的虚拟适应度表示如下：

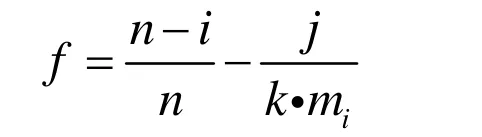
其中，n为种群的级数；im 为第i级的个体数目；k为拥挤距离的影响系数。

4.6 进化操作

本文中，进化操作包括选择、交叉和变异操作。选择操作采用轮盘赌方式进行，不多赘述。下面具体介绍交叉、变异操作。

(1) 交叉操作

本文中借鉴了整个回路基因块交叉的思想[4]，即将表征整个回路状态的基因块作为一个整体，进行交叉操作。在父、母本均可行的情况下，这种交叉方式能较好地避免不可行个体的产生，但在回路之间公共支路较多的情况下，仍有可能产生较多不可行个体，本文对此作了改进：

① 选择父本的n个回路基因块，直接复制到子代，并剔除母本中的这n个基因块；

② 在母本中寻找与所剔除的基因块无公共支路的基因块，将其复制到子代，并在母本中剔除；

③ 将母本的剩余基因依次与子代拓扑结构相比较，若形成环网或孤岛，将其状态置反；否则无操作。比较完成后，将其全部复制到子代。

(2) 变异操作

本文中，变异操作在回路基因块内部完成。首先选定某一基因块，在不表征回路之间公共支路的基因中，随机选择两个，将其基因值互换。

上述交叉和变异操作可以完全避免不可行个体的产生，保证较高的优化效率。

5 算例分析

本文采用IEEE33节点配电系统算例[12]。如图2所示，其中有37条支路，33个节点，5个联络开关，额定电压为12.66kV，总负荷为3715kW+2300kvar。DG的并网节点和注入功率见表1。

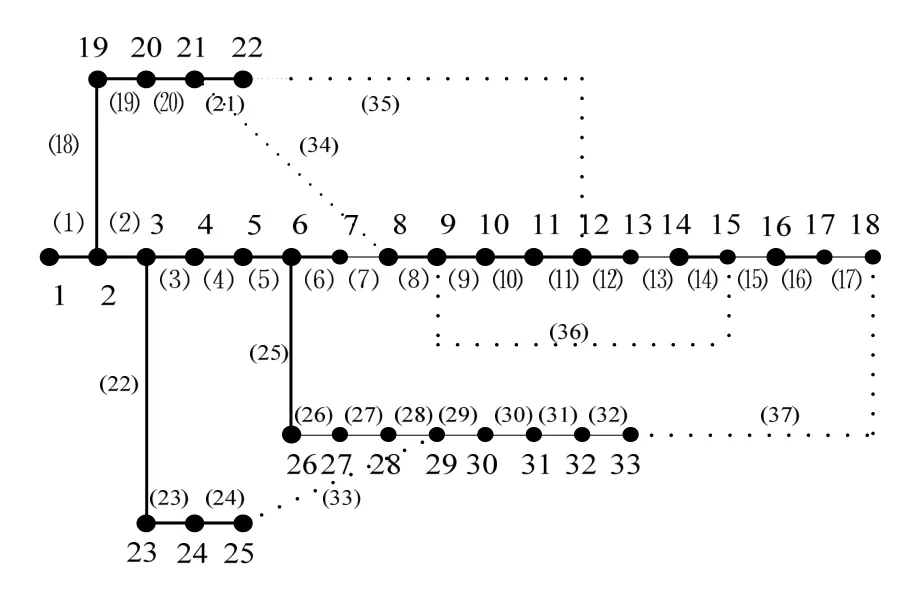
图2 IEEE33节点配电系统

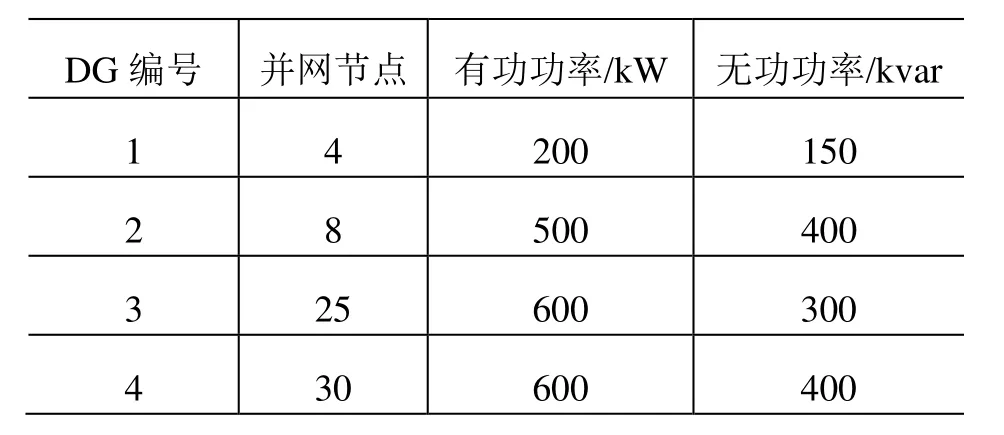
表1 DG并网节点和容量

本文采用MOGA进行求解，最终所得的Pareto最优解及运行时各代出现的Pareto最优解分布情况分别如表2和图3所示。

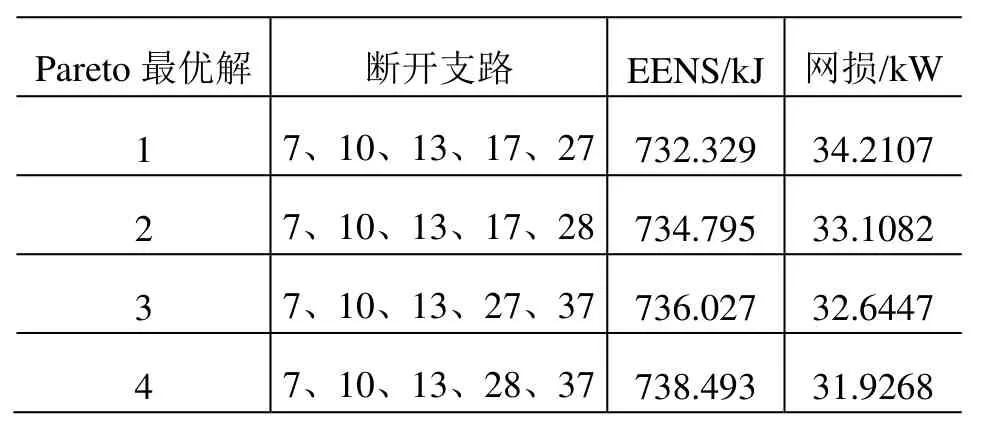
表2 Pareto最优解

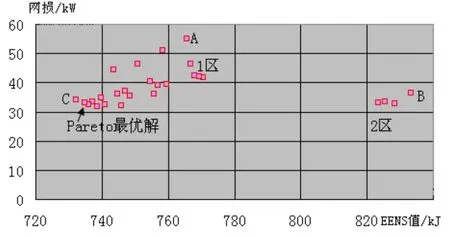
图3 历代Pareto最优解分布图

分析：

(1) 配电网络闭环设计、开环运行、EENS值及网损值均与各馈线之间的负荷平衡度有关，不同的是，前者考量的是各馈线负荷与故障率之间关系，后者主要受到各馈线负荷与阻抗之间关系的影响。如图2所示，1区和2区的解个体在EENS值和网损值上相差较大，分别取1、2区的代表个体A、B进行分析，前者的断开支路为4、11、12、28、32，后者为10、12、33、34、37。可以看出，个体A、B的网络结构差异不大，主要差异在于个体A的节点5~18的负荷由支路1、18~20、34供给，而个体B则主要由支路1~7供给，前一条供电路径的故障率较低、阻抗较大，后一条供电路径的故障率较高、阻抗较小，这样造成了个体A的EENS值远远低于个体B，而网损值远远高于个体B。

(2) 从Pareto最优个体中选出个体C，与个体A进行对比。个体C的断开支路为7、10、13、17、27，其供电路径与个体A基本一致，不同之处在于：个体C的节点5、6、26、27的负荷由支路1~4供给，而个体A由支路1、18~20、34供给，由于节点4上安装了200kW+j150kvar的DG，在个体C对应的网络结构中，节点5、6、26、27的负荷可以由该DG供给，稳态运行时降低了功率传输的网损，故障时形成含DG孤岛继续供电，降低了EENS值。因此个体C的EENS值和网损值均远远低于个体A。

6 结语

本文提出基于MOGA的含DG配电网络多目标重构方案，可以得到同时具有较好安全供电能力和稳态经济运行能力的网络结构。本文考虑了 DG对EENS值和网损值的影响，不足之处在于将DG看作恒定出力的电源，实际上许多DG的运行状态受系统状态影响较大，以后研究中可将其建立为动态模型，考虑更为复杂的情况。

[1] 张栋,张刘春,傅正财.配电网络重构的快速支路交换法[J].电网技术,2005,29(9):82-85.

[2] 王超学,崔杜武,崔颖安,等.使用基于中医思想的蚁群算法求解配电网重构[J].中国电机工程学报,2008,28(7):13-18.

[3] 许立雄,吕林,刘俊勇.基于改进粒子群优化算法的配电网络重构[J].电力系统自动化,2006,30(7):27-30.

[4] 毕鹏翔,刘健,刘春新,等.配电网络重构的改进遗传算法[J].电力系统自动化,2002, 26(2):57-61.

[5] 崔金兰,刘天琪,李兴源.含有分布式发电的配电网重构研究[J].电力系统保护与控制,2008,36(15):37-40.

[6] 陈焕飞,刘朝,贾宏杰,等.基于 Bender’s分解的含 DG 配电系统网络重构[J].电力系统自动化,2008,32(21):22-26.

[7] 李传健,刘前进.考虑风力发电随机性的配电网重构[J].电力系统自动化,2010,34(20):34-39.

[8] 何禹清,彭建春,文明,等.含风电的配电网重构场景模型及算法[J].中国电机工程学报,2010,30(28):12-18.

[9] 张鹏,王守相.提高系统可靠性的配电网络多目标重构区间方法[J].电力系统自动化,2004,28(21):22-26.

[10] 余健明,蔡利敏,杨文宇.基于提高系统可靠性降低网损的配电网络重构[J].电工技术学报,2004,19(10):70-73.

[11] 王守相,张鹏.兼顾供电可靠性和经济型的多目标网络重构[J].电力系统保护与控制,2005,33(7):16-20.

[12] GOSWAMI S K, BASU S K. A new algorithm for the reconfiguration of distribution feerders for loss minimization[J]. IEEE Trans on Power Delivery, 1992, 7(3):1484-1491.