水下爆炸数值仿真

吴国民，周心桃，肖汉林，段 宏

(中国舰船研究设计中心，湖北 武汉 430064）

水下爆炸数值仿真

吴国民，周心桃，肖汉林，段 宏

(中国舰船研究设计中心，湖北 武汉 430064）

基于MSC.Dytran软件，通过一维球对称数值仿真模型，模拟了水下爆炸冲击波传递以及第一次气泡脉动过程，其计算结果与经验公式计算结果吻合较好，在此基础上讨论了网格划分方式、网格密度以及计算区域大小对计算结果精度的影响。通过一维模型与三维模型数值计算结果的对比，论证了基于一维球对称数值仿真模型，通过Remap映射技术进行三维模型数值仿真的计算方法。该方法在保证计算精度的同时较大地提高了计算效率，具有较强的工程应用价值。

MSC.Dytran;水下爆炸;数值仿真;映射

0 引言

舰艇在执行使命任务的过程中，会受到各种水下爆炸攻击，有水下远场爆炸、水下近场非接触爆炸以及水下接触爆炸等作用工况，因此，舰船抗水下爆炸性能是衡量其生命力的重要指标之一。在进行水下爆炸载荷作用下的舰艇抗爆抗冲击设计时，水下爆炸数值仿真是重要的技术手段之一，通常可利用大型的商用有限元软件进行建模计算，主要的软件有AUTODYN、ABAQUS、LS-DYNA以及 MSC.Dytran，其中MSC.Dytran因为与功能强大的前后处理软件MSC.Patran无缝连接，建模便捷，同时基于任意拉格朗日－欧拉求解方法(ALE）具有强大的流固耦合求解功能，因而被广泛应用于水下爆炸数值仿真分析中［1－2］。国内外科研人员对于如何利用MSC.Dytran进行水下爆炸冲击波传递以及气泡脉动过程数值仿真也开展了深入的研究，如张振华等利用该软件模拟了无限水域中球形药包的水下爆炸冲击波传递过程，并分析提出了通过修改水的状态方程参数提升冲击波压力，以有效降低计算单元数量和计算时间的方法［3］;邓文斌等也对水下爆炸冲击波进行了数值仿真，并提出了优化计算文件节约计算时间提高解题效率的方法［4］;Matsumoto和方斌等则分别利用该软件实现了对水下爆炸气泡脉动的数值模拟，并重点分析了边界条件对气泡脉动压力、脉动周期等特性的影响［5－6］。本文利用 MSC.Dytran软件，通过一维球对称模型对水下爆炸的冲击波传递以及第一次气泡脉动过程进行数值仿真，在此基础上分析提出基于Remap映射技术提高三维模型数值仿真计算效率的计算方法，可为水下远场非接触爆炸作用下的舰船冲击动响应分析提供借鉴。

1 水下爆炸冲击波传递及气泡脉动过程

在无限水域中爆炸冲击波传递的主要过程可分为5个阶段，如图1所示，分别是指数衰减阶段、倒数衰减阶段、倒数衰减后端、第一次气泡膨胀收缩段和脉动压力段。在爆炸起始阶段，冲击波压力在瞬间达到峰值，然后迅速衰减，同时爆炸产生的高压气体形成气泡，开始第一次气泡脉动，先是因内部压力大而膨胀，达到气泡半径最大值后，在外部压力的作用下，气泡开始收缩，当气泡半径收缩到最小时，出现脉动压力峰值，此压力峰值不大于冲击波压力峰值的10%～20%，但脉动压力持续的时间却大大超过冲击波压力作用时间，因此，二者的冲量值大小是相当的［7］。在此之后气泡脉动能量已所剩无几，因此对于工程问题而言，主要考虑爆炸开始到第一次气泡脉动结束这一过程［8］。

图1 水下爆炸冲击波压力时历曲线Fig.1 The time-pressure curve of underwater explosion

对于水下爆炸的前5个阶段，库尔在早期提出的经验公式给出了很好的描述，并经试验验证具有良好的精度，因此一直沿用至今。其中对于冲击波压力峰值及指数衰减阶段用下列公式表示［7］:

式中:Pm为冲击波压力峰值，Pa;W为TNT球状药包质量，kg;R为爆心到测点的距离，m;R0为药包的初始半径，m;θ为冲击波时间衰减常数，s;而第一次气泡的最大半径rmax和脉动周期T分别用下列公式进行计算:

式中z为爆心处的流体静压力水柱值，m。

下节水下爆炸数值仿真将针对上述冲击波传递以及第一次气泡脉动压力过程进行模拟，并与经验公式的计算结果进行对比，以验证数值仿真的精度。

2 数值仿真

对于水下爆炸数值仿真，MSC.Dytran采用欧拉方法进行求解，在时间域上采用显示积分法，在空间上用欧拉单元离散，单元均为一阶单元，可采用8节点任意六面体单元、6节点三棱柱单元和4节点四面体单元。对于欧拉网格中的炸药和流体，分别利用状态方程来定义其压力与密度及比内能之间的函数关系。

2.1 水的状态方程

在绝热条件下，水的状态方程为［9］

式中:p为压力;ρ0为水在常温状态下的密度;ρ为整体密度;B和n为常数，B=3 045 kg/cm2，n=7.15。

在MSC.Dytran中，水的状态方程用多项式状态方程(EOSPOL）来模拟，其中压力是相对体积及比内能的多项式函数［10］:

式中:e为单位质量比内能;μ=(ρ/ρ0）－1。计算中，取p=a1μ，体积模量 a1=2.2 GPa，并取 ρ0=1 000 kg/m3，e=83.950 kJ/kg。

2.2 TNT的状态方程

在MSC.Dytran中，用JWL状态方程(EOSJWL）来模拟炸药爆炸过程:

式中:η=ρ/ρ0，ρ0为炸药的初始密度，ρ为材料整体密度;e为单位质量比内能;A，B，ω，R1及R2为常数。对于TNT炸药，密度为1 580 kg/m3，比内能为4.19MJ/kg，初始爆轰波速度为6 930m/s，A=371.2 GPa，B=3.231 GPa，ω =0.3，R1=4.15，R2=0.95。

2.3 计算工况

假定在静止的水域中，水深40 m处，1 kg的TNT球形炸药(药包半径为0.053 3 m）在水中爆炸，水面的大气压为1.01×105Pa，计算分析在离药包中心0.4～1.0 m范围内的冲击波衰减特性以及水下爆炸第一次气泡脉动的最大半径和周期。

1）一维球对称计算模型

在上述计算工况中，水深相对于药包的直径为大值，且在爆源附近的爆炸冲击波作用过程为毫秒级的强间断，可以近似地认为爆源附近的冲击波传递为1个球对称过程。因此，可用一维球对称模型在MSC.Dytran中进行计算分析。

建立一维球对称模型如图2所示，坐标原点为爆心，沿x方向建模，楔形夹角为2°，水域长为30m，从爆心到水域边界采用bias网格划分方法，由密到疏共划分6 000个欧拉单元，在x方向上最大单元与最小单元尺寸之比为3，在x=30 m的水域边界处设置流入流出边界条件。计算时间为0.10 s，对于一维球对称模型在考虑计算时间步长时，只考虑径向单元的尺寸。在x=0.4～1.0 m范围内均匀设置7个考核点，以记录冲击波传播过程和衰减规律。

图2 一维球对称模型局部放大图Fig.2 The local view of1－D spherical symmetrymodel

在x=1.0 m处考核点记录的冲击波压力时历曲线如图3所示。该曲线反映了冲击波的衰减和第一次气泡脉动的典型过程，图4给出了x=1.0 m处冲击波压力衰减曲线与经验公式计算结果的对比，图5则给出了x=0.4～1.0 m共7个考核点的冲击波压力峰值与经验公式结果的对比，从图上可以看出二者很吻合。

图6给出的是由第一次气泡体积转化得到的气泡半径的变化时历曲线。从上述结果可知，当t=0.035 8 s时，第一次气泡脉动的气泡半径达到最大值rmax=0.864 m，而第一次气泡脉动周期为T=0.069 5 s。上述计算结果与经验公式的比较见表1，误差在10%以内。

图6 气泡半径的时历曲线Fig.6 The time-radius curve of the bubble's impulse

表1 第一次气泡脉动特性对比Tab.1 The comparison of the first bubble's impulse

2）三维计算模型

一维球对称模型由于单元少因此计算效率很高，同时上述分析表明其计算精度也在工程误差范围内，但应用到工程问题一般都需要建立三维模型进行计算分析，MSC.Dytran提供了从一维模型计算结果到三维模型的Remap映射技术。下面将首先建立三维模型进行计算，然后将一维模型与三维模型的计算结果进行对比，再利用Remap映射技术，将映射后的三维模型计算结果与直接用三维模型计算的结果进行对比，以论证一维球对称模型在工程问题中应用的可行性。

为了使三维模型网格密度与一维球对称模型一致，选取建立0.502 7 m×0.502 7 m×0.502 7 m的立方体水域三维模型，坐标原点为爆心，同样是球形TNT装药1 kg，分别沿x，y及z向用bias网格划分方法划分181个六面体单元，共计5 929 741个单元，最大单元尺寸与最小单元尺寸之比为1.033 3，边界条件及状态方程与一维球对称模型一致。

图7给出了t=0.16 ms时刻一维模型与三维模型的计算结果对比，选取的是压力、速度、比内能以及密度在x方向上的分布曲线对比，从图中可以看出，在离爆心较近的区域尤其是1倍药包半径范围内，2种模型中的计算结果有一定差异，这是由于爆轰波的初始模拟对网格较敏感，爆心越近，单元网格差异越大，尤其在爆心处，一维模型为4个节点共用的五面体锥形单元，而三维模型为规整的六面长方体单元，单元的差异导致离爆心较近区域的计算结果差异较大，而在1倍药包半径范围外，2种模型的计算结果吻合得很好。

3）一维模型向三维模型的映射

所谓一维模型向三维模型的映射，是指先利用一维球对称模型计算爆炸起始时刻t0到某一时刻t1，选取的t1必须是流体介质尚未完全流出计算区域的时刻，提取t1时刻一维球对称模型计算结果中沿径向的密度、比内能以及速度分布曲线(如图7所示），并以数据对的形式分别存储成*.xyd文件，然后在三维模型的*.dat文件中手工添加TABFILE语句调用上述*.xyd文件，计算时将上述密度、比内能以及速度分布映射到三维模型中，作为三维模型计算的第1个载荷步，即若三维模型需要求解的总的时间段为t0～t2时刻，前面的t0～t1时刻用一维模型计算，将t1时刻的计算结果导入三维模型，利用三维模型接着进行t1～t2时刻的计算分析，用上述接力方式达到大大节约计算时间、提高求解效率的目的［10］。

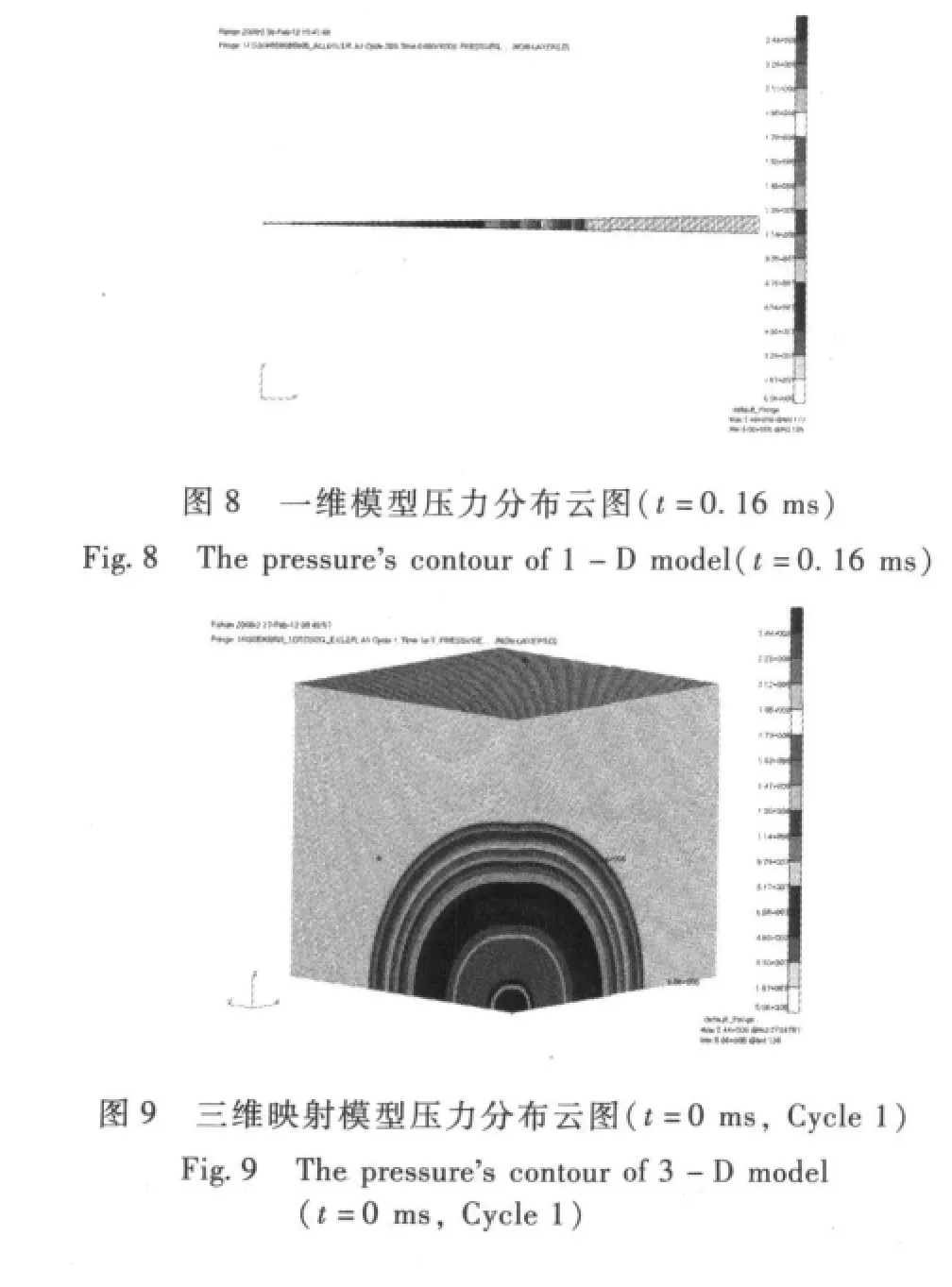
图8给出的是t=0.16 ms时刻一维模型压力分布云图，其冲击波阵面到达x=0.131 m处，将上述时刻的计算结果映射到三维模型中，如图9所示，三维模型的第1个载荷步的压力分布云图与一维模型的完全一致，在此基础上三维映射模型计算到t=0.02 ms时刻的压力分布如图10所示，此时相对于起爆点的绝对时刻为t=0.16+0.02=0.18 ms;直接用三维模型进行求解到t=0.18 ms时刻的压力分布如图11所示。由图10与图11进行对比，二者的压力分布规律和最大值以及冲击波阵面到达位置均非常一致。而在同样的软硬件条件下，上述直接用三维模型求解所耗的机时是利用映射技术求解所耗机时的10倍以上。因此，基于一维模型计算结果，利用映射技术，再建立三维映射模型进行求解，大大提高了计算效率，同时计算精度有所保证。

3 一维球对称模型数值模拟影响因素

3.1 网格划分方式对计算结果的影响

在建立一维球对称模型时，网格划分方式有非均匀划分和均匀划分2类，非均匀划分即如上节中用bias网格划分方法进行单元划分，靠近爆心处的网格相对较密;均匀划分即所有的单元在x方向的尺寸一致。如图2所示的模型，在30 m区域内分别用非均匀和均匀2种方式划分6 000个单元，在其他条件相同的情况下，在x=0.4～1.6 m的范围内，二者的压力计算结果对比如图12所示。非均匀划分网格方式的计算结果与经验公式计算结果更接近，二者计算所得第一次气泡脉动最大半径和周期差别不大，说明用非均匀网格划分方式的计算精度更高。

图12 不同网格划分方式压力计算结果对比Fig.12 The comparison of the x－Pressure curves calculated with differentmethods ofmeshing

3.2 网格划分密度对计算结果的影响

如图2所示的一维球对称模型，在30 m区域内采用同样的网格划分方式，即在x方向上最大单元与最小单元尺寸之比为3，分别划分2 000，4 000，6 000，8 000以及10 000个单元，在其他条件相同的情况下，在x=0.4～1.6 m的范围内，压力计算结果对比如图13所示，可以看出网格密度在6 000和8 000的压力计算结果，比其他网格密度的结果更为接近经验公式结果;气泡脉动特性对比如表2所示，计算表明网格越密，气泡脉动周期和半径就越小。

图13 不同网格密度压力计算结果对比Fig.13 The comparison of the x－pressure curves calculated with different densities ofmesh

表2 不同网格密度的第一次气泡脉动特性对比Tab.2 The comparison of the characters of the first bubble's impulse with different densities ofmesh

3.3 计算区域大小对计算结果的影响

分别建立10，20，30和40m区域的一维球对称计算模型，每个模型在x=10 m以内的范围按bias网格划分方式划分2 000个单元，即在x方向上最大单元与最小单元尺寸之比为3，x=10 m以外的范围按同样的单元尺寸进行均匀划分。计算结果表明，在x=0.4～1.6 m的范围内，压力计算结果完全一致，不受计算区域大小的影响，但是气泡脉动特性受计算区域影响较大，如表3所示，计算区域越大，气泡半径和脉动周期就越大，越接近经验公式计算值，这说明虽然计算模型中在边界处定义了流入流出的边界条件，但是计算区域过小还是会有边界反射效应，影响气泡特性的计算精度。

表3 不同计算区域的第一次气泡脉动特性对比Tab.3 The comparison of the characters of the first bubble's impulse with different ranges of the numericalmodel

4 结语

通过上面的计算分析，可以得到以下结论:

1）一维球对称模型可以较好地模拟无限水域条件下水下爆炸冲击波传递以及第一次气泡脉动过程，数值仿真得出的冲击波压力、第一次气泡脉动半径和周期均与经验公式能较好地吻合。

2）同等网格密度及其他边界条件下，一维球对称模型与三维模型在水下爆炸数值仿真中所得的冲击波压力、速度、比内能以及密度分布在药包半径范围内有一定的差异，但在药包半径范围外二者的计算结果基本一致。

3）基于一维模型计算结果，利用Remap映射技术进行三维模型数值仿真的计算方法，大大提高了求解效率，同时计算精度有所保证。上述计算方法在工程应用上很有意义，如对于图14所示的水下远场非接触爆炸作用下舰船冲击响应分析问题，在冲击波阵面传递到离船体一定距离产生边界反射效应前，其冲击波传递过程可用无限水域下的水下爆炸冲击波传递规律模拟，可利用上述计算方法，先用一维模型模拟上述冲击波阵面的传递过程，然后利用映射技术进行后续的三维模型数值仿真计算，不但解决了因远场水下爆炸仿真模型水单元数量巨大而无法计算的问题，而且计算效率大大提高。

图14 冲击波加载示意图Fig.14 The illustration of loading shock wave

4）利用一维模型进行数值计算时，采用非均匀的bias网格划分方法进行单元划分，靠近爆心处的网格相对较密，计算精度更高;网格密度对冲击波压力和气泡脉动特性计算值有一定影响，网格单元尺寸要适中，单元尺寸过小或过大，都会使在被考核的距离范围内冲击波压力值偏离经验公式的计算结果，而第一次气泡脉动半径和周期则是随着网格密度的增大而减小，因此需要针对关注的具体问题选择合适的网格密度;而在同等网格密度下，计算区域大小对冲击波压力计算值几乎没有影响，但对气泡脉动特性有影响，计算区域越大，边界反射效应影响越小，气泡半径和脉动周期计算值越准确。

［1］尹群，陈永念，等.水下爆炸研究的现状和趋势［J］.造船技术，2003，(6）:6－12.

［2］李磊，冯顺山.水下爆炸对舰船结构毁伤效应的研究现状及展望［J］.舰船科学技术，2008，30(3）:26－30.

LILei，FENG Shun-shan.Present state and perspectives of damage effect to ship construction subjected to UNDEX［J］.Ship Science and Technology，2008，30(3）:26 －30.

［3］张振华，朱锡，白雪飞.水下爆炸冲击波的数值模拟研究［J］.爆炸与冲击，2004，24(2）:182－188.

［4］邓文彬，王国治.基于DYTRAN软件的水下爆炸数值计算［J］.华东船舶工业学院学报(自然科学版），2003，17(6）:11－16.

［5］MATSUMOTO.Boundary curvature effects on gas bubble oscillations in underwater explosion［R］.ADA308087，1996.

［6］方斌，朱锡.不同边界条件下水下爆炸气泡的数值模拟［J］.海军工程大学学报，2008，20(2）:85－90.

FANG Bin，ZHU Xi.Numerical simulation of underwater explosion bubble with different boundaries［J］.Journal of Naval University of Engineering，2008，20(2）:85 －90.

［7］库尔.水下爆炸［M］.罗耀杰，等译，北京:国防工业出版社，1960.6－9.

［8］姚熊亮.舰船结构振动冲击与噪声［M］.北京:国防工业出版社，2007.144－151.

［9］J.亨利奇.爆炸动力学及其应用［M］.熊建国，等译，北京:科学出版社，1987.59 －62.

［10］MSC.Dytran User's Manual［M］.MSC Corporation，2008.

Numerical simulation of underwater explosion

WU Guo-min，ZHOU Xin-tao，XIAO Han-lin，DUAN Hong
(China Ship Development and Design Center，Wuhan 430064，China）

Using the software MSC Dytran，the shock wave's spread and the first bubble's impulse in underwater explosion were simulated by 1-D spherical symmetry numericalmodel.The results of numerical simulation were agreeable with the ones of experimental formulations.The factors influencing on the calculation resultswere compared and analyzed，such as the method ofmeshing，density ofmesh and the range of the numericalmodel.Through comparing the calculation results of 1-D model with the ones of 3-D model，the calculation method of translating 1-D spherical symmetry model into 3-D model by Remap was proved out.The above method improved the efficiency of numerical simulation，and also ensured the necessary precision，so itwas significant to the actual engineering problems.

MSC.Dytran;underwater explosion;numerical simulation;Remap

E925.2

A

1672－7649(2012）09－0020－07

10.3404/j.issn.1672－7649.2012.09.004

2012－03－19;

2012－04－10

吴国民(1980－），男，博士研究生，工程师，从事水面舰船结构抗爆抗冲击设计工作。