基于松弛技术的重频密频结构模态灵敏度分析

张 淼， 于 澜， 鞠 伟

（1.长春工程学院 理 学院，吉林 长 春 130012；2.中国第一汽车股份有限公司 技 术中心，吉林 长 春 130011）

0 引 言

大型空间柔性结构振动的一个主要特点就是固有频率低而且密集，其中一个难点就是如何控制轻阻尼的模态密集型结构，常见的方法是将密集模态处理成为重频模态来研究控制器的设计［1－4］。由于频率密集时，对应的单个模态往往呈现病态，极可能出现不稳定现象，所以很难确定，因此单特征值的灵敏度分析方法已不适用［5－7］。而对于完备的重频系统，特征子空间是良态的，容易确定，并可用于计算其相应的灵敏度。当把重频系统得到的控制规律应用到密频系统时，必须考虑由此产生的误差及重频模态的敏感性问题。

文献［8］分析了模态不稳定性对密频系统控制性能的影响及溢出问题，并给出了密频系统的参数自调整模糊振动控制方法。文献［9］研究了重频系统状态估计器的方法。文献［10］给出了密频子空间可控度和可观度的小参数方法。

目前用全模态方法分析密集模态敏感性问题仍未妥善解决，本文通过引入松弛因子的技术建立重频系统模态灵敏度算法，进而分析了重频、密频模态对灵敏度矩阵的影响程度。

1 完备系统的灵敏度分析

对N自由度的线性振动系统，即

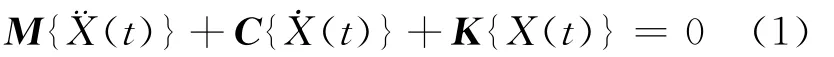
其中，M、C和K∈RN×N分别为系统的质量、阻尼和刚度矩阵，它们并没有强加传统的对称正定条件的限制，但假定M－1存在。

对第i个特征对（λi，ui），λi是第i个复特征值，ui是相应于λi的复特征向量，并满足方程Mui＋λiCui＋Kui＝0（∀i＝1，…，2N）。

假设系统（1）可以被一系列m个设计参数g＝（g1，g2，…，gm）T所描述，这里gi可以是梁截面、板厚度等参数，g称为设计向量，则M、C和K可以都是关于设计向量g的函数。当系统修改时，设计向量g发生扰动，记

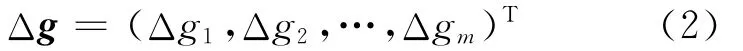
其中，Δgi（i＝1，…，m）是第i个设计参数的扰动量。记ui扰动后的形式为，取其线性部分，得

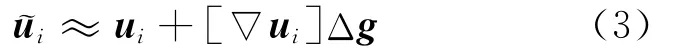
其中，［▽ui］＝［ui，1，ui，2，…，ui，m］为N×m阶矩阵，称为特征向量灵敏度矩阵，ui，j＝∂ui／∂gj表示ui对第j个参数gj的变化率。

为了确定灵敏度矩阵，需分别计算得到ui，j（j＝1，…，m）。

由于系统（1）的状态矩阵为：

则相应的特征问题为：

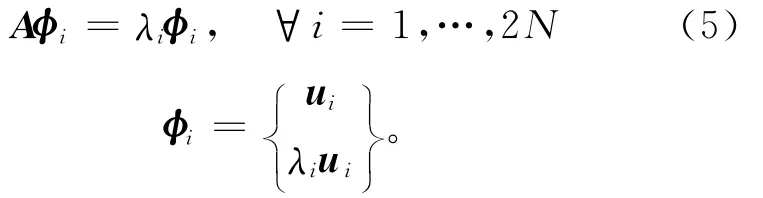
定义：

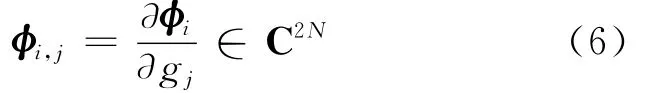
利用完全的状态空间系统展开定理，有

其中，φk为矩阵A的特征空间的基底为展开系数。文献［11］给出了单特征值系统的灵敏度分析的展开式系数的计算公式，但由于其公式的分母中含有λi－λk项，所以当系统对应重频或密频状态时，此类计算公式将会失效。

将（5）式两边关于第j个参数gj求导，得

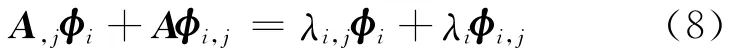
整理得：

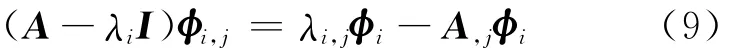
将（7）式代入（9）式，有

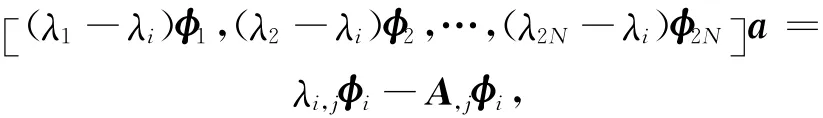
或写成：

其中

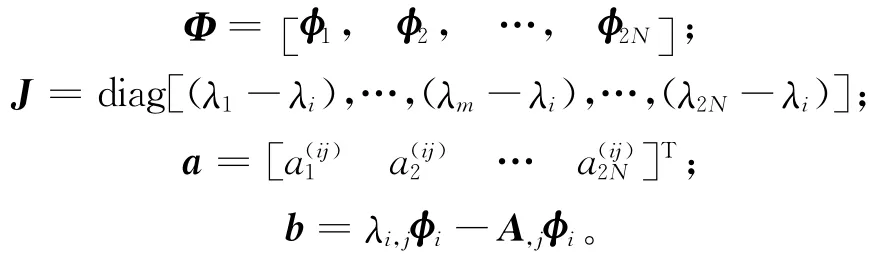
这里λi，j、φi及A，j为已知，当系统（1）完备时，模态矩阵Φ可逆，则（10）式可表示为：解耦（11）式，可分别计算求解得到系数，将其代回（7）式，并取其前N维就得到了模态灵敏度向量ui，j。

2 松弛因子的选取原则

由于（11）式中对角矩阵J奇异，若λk（k＝1，…，2N）为单特征值时，秩数rank（J）＝2N－1，因此，（11）式为亚定方程组或超定方程组，其解始终无法唯一确定，甚至可能无解。

为了解决这个问题，对于固定的k引入松驰因子ω（ω＞0），令

代入（11）式，得

实验组总体健康、生理功能、社会功能、活力、生理职能、情感职能、躯体疼痛和精神健康方面和对照组实验数据间均存在着明显的差异,且P<0.05,具备统计学分析意义。见表1。

若λk为m重特征值，而其他特征值均为单特征值时，秩数rank（J）＝2N－m，此时系数对角阵J中会出现m个零对角元，（11）式中就有m个组合系数（d＝1，…，m）不能确定。用类似前面的分析方法，引入松弛因子ω，显然当i≠k时的系数是精确的，而i＝k对应的系数是要通过简单优化近似得到的，这时最佳松弛因子ω＊收敛准则可选择为：

其中，ηtol为允许误差界。由于对角阵的解耦性能，这种方法对其他系数（m≠k）的求解不会产生任何影响。

3 敏感模态的变化规律分析

由（12）式可知，当ω较小时，特征子空间即为密频子空间，ω→0的过程，正是由密频至重频的转换过程，（7）式中的组合系统可以反映模态敏感状态。从（13）式可以看出，当ω越小时的值相对而言就会越大，与它对应的模态在灵敏度中的贡献就会越大。

由此分析可知，重频模态具有高度的敏感性，它们相对于其他频率模态而言对灵敏度的贡献最大，这是因为它们在灵敏度的线性组合式中的组合系统的权重最大。

而对于密频系统，随着频率密集程度的增加，密集模态的敏感性程度提高。

4 数值算例

4.1 模态敏感性分析算例

在一个5－自由度的质量弹性阻尼系统中，假设只在垂直方向上产生振动，如图1所示。

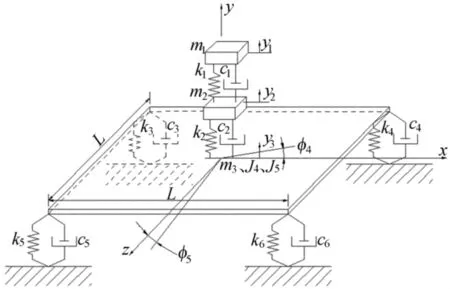
图1 5－自由度非比例阻尼系统

系统质量阵的元素为：

阻尼矩阵的元素与刚度矩阵的元素有类似的形式。例如，c11＝c1；c12＝ －c1；c13＝c14＝c15＝0；c22＝c1＋c2，等。

对应初始系统的状态矩阵A，求得初始系统的特征值，见表1所列。

表1 初始系统的特征值

从表1中可以看出，第7、第9和第8、第10为2对复数的重特征值。为便于说明，本文以重特征值第7和第9个为例，设计变量取k5，变化率为Δk5／k5＝0.01，求解其特征向量灵敏度。

根据（11）式，J是秩数为2N－2的对角阵，其主对角元见表2所列。

表2 矩阵J的主对角元

通过求解单个解耦方程，直接计算出J方程组中除第7个和第9个以外的所有展开系数7，9）。而为计算a（ij）7、a（ij）9，根据本文提出的引入松弛变量ω技术，就可得到全部展开式系数a（ij）k。表3所列给出了松弛因子ω＝0时的精确解和ω＝1，0.1，0.000 1所得到的解。

表3 灵敏度系数对比

从表3中可以看出，当m≠7，9时，引入松弛变量后所得到的新解中与精确解中完全一致，而随着ω的变化与的变化也呈现出明显的规律，即ω越小与的数值越大，这说明其对应模态的敏感性越强，在系统摄动量中的贡献就越大。

4.2 模态灵敏度分析算例

考虑文献［9］中给出的弹簧质量系统，如图2所示。

图2 弹簧质量系统

其中，k1＝0.95；k2＝k3＝…＝k10＝0.03；k11＝1.05；m1＝m2＝…＝m10＝1.0，每个频率的自然阻尼系数都为0.05。

用有限元方法提取系统的性质矩阵后，经计算得到初始系统的前10个特征值和以k11为设计参数，用本文方法所得到的前10阶模态灵敏度近似值，结果见表4所列，表4中，‖ui，k11‖为模态灵敏度值。

从表4中可以看出，系统的第9及第10特征值十分接近而构成一个密集频率子空间，并由本文所得到的灵敏度值可知，第9阶与第10阶模态关于参数k11的振动稳定性较差，这与文献［9］中的结论一致。

表4 系统特征值及模态灵敏度值

5 结束语

由于重频或密频的影响，在模态灵敏度算法中需要求解一种可能为亚定或超定方程组，但由于其系统阵已化为对角阵，所以很容易分析其性态。本文通过引入松弛因子的技术，提出一种精确而简便的求解亚定或超定方程组的方法，并给出其收敛准则及误差估计方法。该方法不仅适用于单频系统，还适用于重频系统的灵敏度分析，为密频系统的振动控制等研究工作提供了良好的理论模型。

通过重频系统的灵敏度分析，得到了重频模态具有高度敏感性的结论，它们相对于其他频率模态而言对灵敏度的贡献最大。而对于密频系统，随着频率密集程度的增加，其模态的敏感性程度也随之提高。数值算例验证了该方法的有效性。

［1］ Abe M.Vibration control of structures with closely spaced natural frequencies by a single actuator［J］.Journal of Vibration and Acoustices，1998，120（1）：117－124.

［2］ 刘一武，张洪华，吴宏鑫.可控性差的空间密集模态的结构的振幅最优控制［J］.自动化学报，2002，28（2）：1－6.

［3］ Sun H L，Zhang P Q，Chen H B，et al.Active control of a structure with continuously closely spaced natural frequencies ［J］.Journal of Sound and Vibration，2006，294：15－22.

［4］ 程 琳，谢 峰.一种基于振动的汽车主减总成在线故障诊断系统［J］.合肥工业大学学报：自然科学版，2011，34（8）：1138－1141.

［5］ 刘利军，樊江玲，张志谊，等.密频系统模态参数辩识及其振动控制的研究进展［J］.振动与冲击，2007，26（4）：109－115.

［6］ Moon Y J，Kim B W，Ko M G，et al.Modified modal methods for calculating eigenpair sensitivity of asymmetric damped system［J］.International Journal for Numerical Methods in Engineering，2004，60：1847－1860.

［7］ 解惠青，戴 华.非亏损动力学系统特征对导数的计算［J］.振动工程学报，2004，17（3）：369－373.

［8］ 刘潇翔，胡 军.包含密集模态的空间结构的模糊主动振动控制［J］.空间控制技术与应用，2010，36（4）：18－24.

［9］ 徐博候，鲍荣浩，张阿平.密频系统振动控制的状态估计［J］.力学学报，2000，32（5）：606－612.

［10］ 陈德成，杨靖波，白 浩，等.密频子空间的可控度与可观度［J］.应用力学学报，2001，18（2）：15－19.

［11］ Adhikari S.Rates of change of eigenvalues and eigenvectors in damped dynamics system［J］.AIAA Journal，1999，39（11）：1452－1457.