车桥耦合振动分析的状态空间法

逄焕平， 董满生， 侯超群

（合肥工业大学 交 通运输工程学院，安徽 合 肥 230009）

早在19世纪，很多学者就对桥梁在移动列车车辆荷载作用下的车桥耦合振动分析进行了研究［1－3］。

文献［4］解决了2个基本问题，即常力在梁上的运动和谐振力在梁上的运动。

文献［5］对结构在移动车辆荷载作用下车桥耦合振动问题作了大量的解析研究。

文献［6］推导了用于车桥耦合振动分析的通用车桥耦合单元，基于纽马克有限差分法对耦合方程进行离散，采用迭代的方法进行求解。

文献［7］提出了由移动车轮单元、弹簧阻尼单元、集中质量单元和刚性连接建立复杂车辆模型的方法，其给出的用于车桥耦合分析的车辆模型的特征矩阵为对称矩阵。

本文对车桥耦合单元进行了详细推导，得到了车桥耦合的质量、阻尼和刚度矩阵，并就其求解过程进行了讨论，其方法可以推广到其他复杂桥梁及车辆模型中，具有非常好的实用性［8］。

本文对一经典模型进行了计算分析，与文献［6，9－10］比较，可以看出本文计算方法非常精确。

1 车桥耦合单元的推导

本文采用的车桥耦合计算模型如图1所示，假定车辆模型的质量矩阵为Mv，阻尼矩阵为Cv，刚度矩阵为Kv，则车辆的运动方程为：

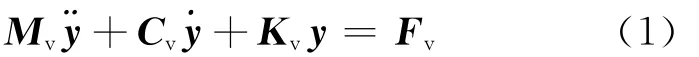
其中，Fv可分为2部分，一部分是作用在车辆模型上的外荷载Fe，另一部分是车桥之间的相互作用力Fc，即Fv＝Fe＋Fc。

由图1可知，所有车辆模型的节点可分为2部分，一部分是不与桥梁直接接触的车体部分，其对应的自由度用yu表示，另外一部分是与桥梁直 接接触的车轮部分，其对应的自由度用yw表示。

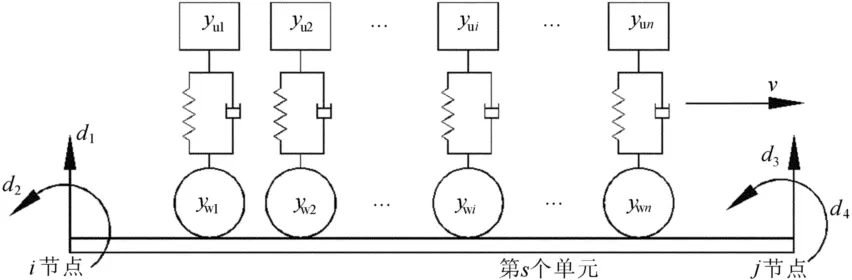
图1 车桥耦合单元示意图

假定作用在车轮和车体上的外荷载分别用Few和Feu表示，车轮与梁单元之间的接触力用fc表示，则对（1）式重新分组排列，可得：

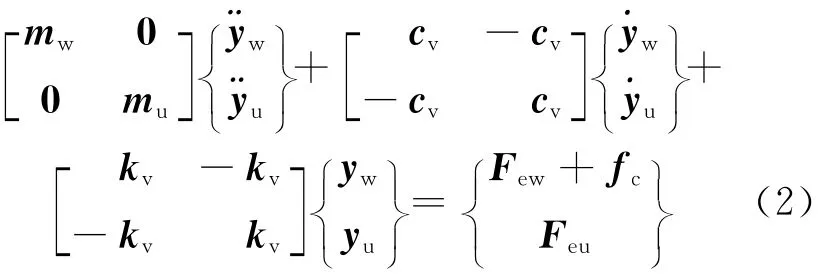
yw与第s个梁单元的节点位移之间可通过厄米特插值函数相互转换，计算如下：

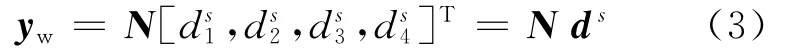
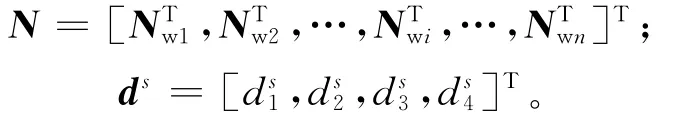
对（3）式时间求一阶和二阶导数，有Nwi（i＝1，2，…，n）为第i个车轮节点对应位置的厄米特插值函数向量，其计算如下：

其中

将（3）～（5）式代入（2）式，可得：

（9）式即为车桥耦合的运动方程［11］。

2 车桥耦合的状态空间法

有车桥相互作用的梁单元运动方程为：

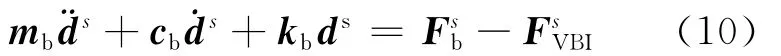
其中，mb、cb、kb为 第s个梁单元的质量矩阵、阻尼矩阵和刚度矩阵；为作用在第s个梁单元的外荷载向量，则将（10）式与（9）式迭加，可得车桥耦合单元的运动方程为：

其中

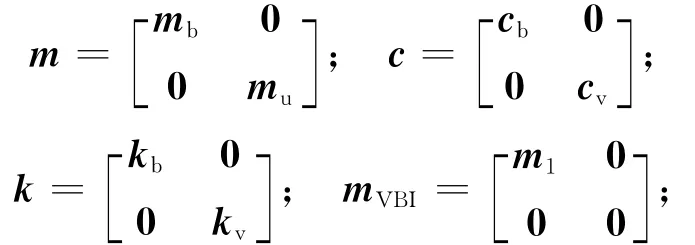
（12）式中的矩阵MVBI、CVBI、KVBI是时变的，整个系统的模态矩阵也是随时间变化的。为简化计算，假定不考虑车桥相互作用时的系统M、C、K的模态矩阵为Φ，频率向量为ω，令 ［dyu］T＝Φq，则可将（12）式转换到模态空间为：

其中

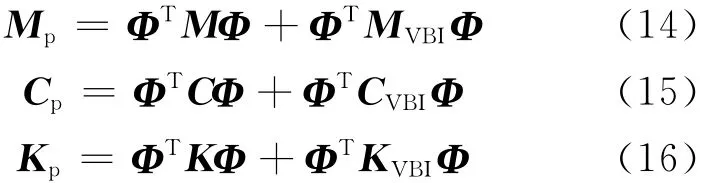
（13）式可进一步改写为：

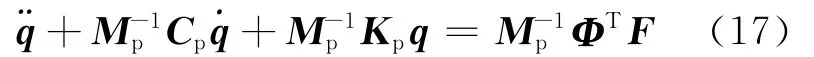
对于复杂模型，其模态矩阵Φ可以通过大型通用软件ANSYS计算得到，通过ANSYS导出的模态矩阵是经过正交化处理的，其中ΦTMΦ是单位阵，ΦTKΦ是对角元素为ω2的对角矩阵，若采用阻尼比为ζ的比例阻尼，则ΦTCΦ是2ζω的对角矩阵。

注意到上面的方程实际上是变质量、变刚度、变阻尼的系统，为方便求解，令z＝［q］T，将其转换为状态空间方程为：

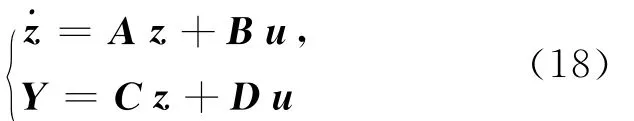
其中

（18）式的变质量、变刚度、变阻尼系统可以通过Matlab的系统仿真模块进行求解，直接得到物理坐标系下各个点的位移及速度响应。计算步骤如下：

（1）t＝0时，给出初始值z0，判断车辆在桥梁上的位置，计算系统矩阵A、B、C和输入向量u。

（2）令tsim＝［t，t＋Δt，t＋2Δt］，利用lsim 求解Δt时刻的值，即

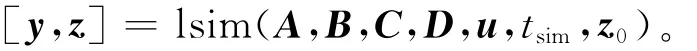
（3）令t＝t＋Δt，判断车辆在桥梁上的位置，如果车辆已经完全移出桥梁，则停止计算；如果车辆没有完全移出桥梁，取步骤（2）中计算结果z的第2列，作为下一步计算的初始值z0，并重新计算系统矩阵A、B、C和输入向量u，转到步骤（2）继续计算。

3 算例验证

算例1 图2所示简支梁长L＝25m，梁的弹性模量E＝2.87×109N／m2，梁的惯性矩I＝2.9m4，梁的质量密度m＝2 303kg／m。

本文计算了简支梁在移动力、移动质量和移动弹簧质量3种模型作用下的响应，其中参数如下：

车辆的移动速度v＝27.78m／s［6－9］。

图2 简支梁的车桥耦合参数图

车辆以27.78m／s速度在简支梁上移动，经过计算可得到梁跨中点的竖向位移、速度和加速度图，如图3所示。所得结果与文献［6，9－10］的结果非常吻合，说明本文方法非常有效。

从图3可以看出，3种不同车辆模型行经桥梁时，所引起的桥梁响应还是有细微差别的。图4所示为移动弹簧质量行经桥梁时簧上质量的竖向位移、速度和加速度响应图。

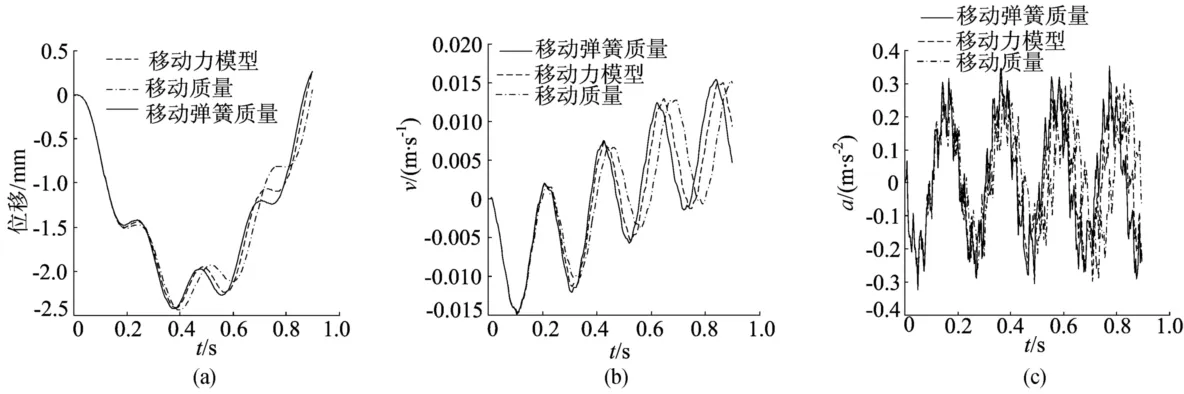
图3 3种车辆模型作用下的竖向位移、竖向速度和竖向加速度图

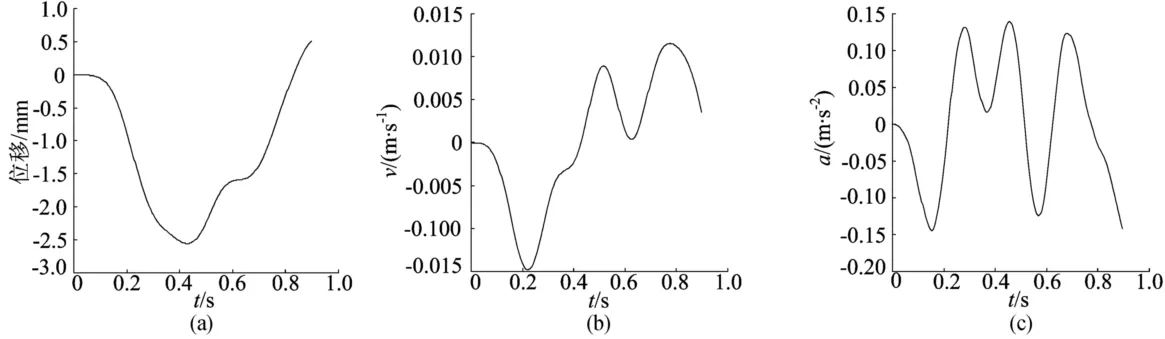
图4 簧上质量的竖向位移、竖向速度和竖向加速度图

算例2 图5所示为文献［12］中的一个算例，该算例为20m＋25m＋60m＋45m的连续梁桥，梁的EI＝9.92×1010N·m2，梁的线质量密度ρm＝11 400kg／m。移动车辆参数为：Mv＝31 700kg，Mw＝3 000kg，kv＝9 120 000N／m，cv＝86 000N／m。

本算例中，车辆的移动速度分别为30、60、90m／s。

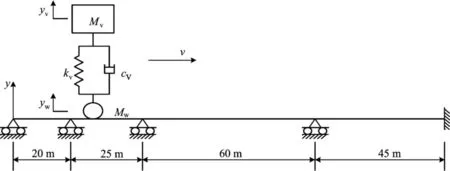
图9 连续梁车桥耦合振动分析示意图

如图6～图7所示，随着速度增加，无论是桥梁响应还是车辆响应均有明显的增加，特别是速度从60m／s增加到90m／s时，75m处最大竖向位移增加了35%左右，车辆移动速度对车辆的影响非常明显，其间簧上质量位移增加了80%，加速度增加了2.5倍左右。这种车桥耦合振动引起的动力效应对桥梁的响应以及行车的舒适性都有着巨大的影响，因此，在桥梁设计时必须考虑移动车辆荷载的移动效果。

图6 梁75m处在不同移动速度时竖向位移与加速度图

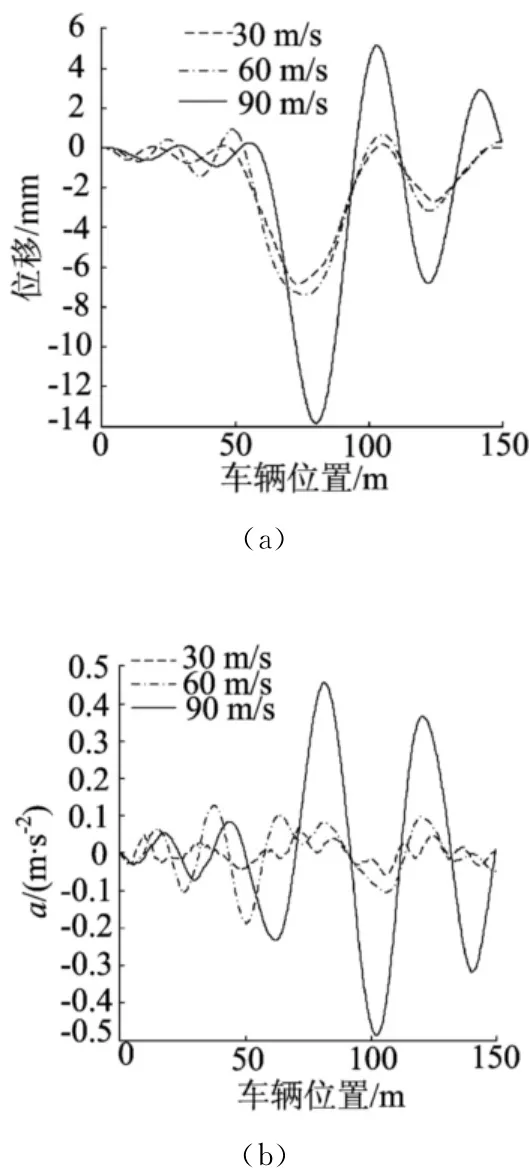
图7 车辆簧上质量不同移动速度时竖向位移和加速度图

4 结束语

本文将时变的线性动力系统分解成时变的线性动力系统和时不变的线性动力系统的叠加，利用时不变的线性动力系统的模态矩阵降低分析的维数，同时利用状态空间理论建立了车桥耦合振动有限元法分析的状态空间法。

该方法具有很高的计算效率和精度，借助于ANSYS和Matlab可以非常方便地应用于复杂桥梁及车辆模型分析计算中。

［1］ Timoshenko S P.On the forced vibration of bridges［J］.Philosophical Magazine，1922，43：1018－1019.

［2］ Lowan A N.On transverse oscillations of beams under the action of moving variable loads［J］.Philosophical Magazine，1935，19（27）：708－715.

［3］ Ayre R S.Jacobsen L S.Transverse vibration of a two－span beam under the action of a moving alternating force［J］.Journal of Applied Mechanics，1950，17（3）：283－290.

［4］ Timoshenko S P，Young D H.Vibration problems in engineering［M］.New York：D Van Nostrand，1955：3－100.

［5］ Fryba L.Vibration of solids and structures under moving loads［M］.Groningen，The Netherlands：Noordhoff International Publishing，1972：3－20.

［6］ Yang Y B，Wu Y S.A versatile element for analyzing vehicle－bridge interaction response［J］.Engineering structures，2001，23：452－469.

［7］ Ju S H.A simple finite element model for vibration analyses induced by moving vehicles［J］.International Journal for Numerical Methods in Engineering，2006，68：1232－1256.

［8］ 蒋培文，贺栓海，王凌波.车辆相互作用对连续梁车桥耦合振动影响分析［J］.合肥工业大学学报：自然科学版，2011，34（8）：1222－1226，1236.

［9］ Zhang Qilin.Numerical simulation of train－bridge interactive dynamics［J］.Computers and Structures，2001，79：1059－1075.

［10］ Michal Majka.Effects of speed，load and damping on the dynamic response of railway bridges and vehicles［J］.Computers and Structures，2008，86：556－572.

［11］ Cheng Y S，Au F T K，Cheung Y K.Vibration of railway bridges under a moving train by using bridge－track－vehicle element ［J ］. Engineering Structures， 2001，23：1597－1606.

［12］ Karoumi R.Response of cable－stayed and suspension bridges to moving vehicles［D］.Stockholm：Royal Institute of Technology，1998.