染料敏化TiO2纳晶体系激发态振动相干效应对光致电子转移速率的影响
蒋礼林 卢喜银 宋云飞 刘伟龙 杨延强,*
(1哈尔滨工业大学物理系,凝聚态科学与技术研究中心,哈尔滨150001; 2贺州学院物理与电子信息工程系,广西贺州542800)
1 引言
位于染料敏化TiO2纳晶体系界面处的光致各向异性电子转移动力学是近年来研究的热门领域,1-3如韩克利研究组4从理论和实验两方面研究了染料在氢键给体溶剂中分子间氢键相互作用对光致电子转移的影响,取得了显著的成果;再如,中国科学院合肥物质科学研究院戴松元课题组,5中国科学院长春应用化学研究所高分子物理与化学国家重点实验室王鹏课题组6都在染料敏化太阳能电池取了显著的成果;最近,我们7对5(6)-羧基荧光素敏化TiO2纳米粒子的光致电子转移的荧光特性研究也取得了一些有益的结果.光致电子转移动力学基本过程的理解对于大量基于纳米粒子器件的研制、开发和应用至关重要,如分子电子学和染料敏化太阳能电池等.8,9
Willig研究组10-15是首先研究界面电子转移的团队之一,由于二萘嵌苯染料分子与TiO2纳晶之间有很强的键连作用,所以能够形成电荷转移复合物.该研究组对上述体系所做的一等系列实验和理论研究获得了显著的成绩,并对电子注入动力学的机制提出了很有见解的观点.该研究组通过对改良的二萘嵌苯敏化TiO2纳晶体系的电子转移飞秒激光光谱的研究表明,由泵浦脉冲在给体激发态中产生的相干波包能幸存于电子转移过程中,并能通过探测脉冲在阳离子形成过程中被监测到;由于传统电子转移理论认为电子转移反应起始于给体中振动模的热平衡布居,因而这些实验结果与之相冲突进而推动了电子注入动力学实时理论的研究.最近,已经提出了好几个理论来阐述在给体-受体中同时存在分子量子拍的相关电子转移.16-19Ramakrishna等20基于有限宽半导体导带、重组能和电子耦合强度、电子注入能级的位置、激发态中不同的初始振动波包和两个振动模参与电子转移过程的5个因素提出了进入有限电子-振动准连续带中同时存在振动相干波包衰减的超快光致各向异性电子转移理论.实验和理论研究表明,激发态振动能级间的相干振动作用不仅能够引起拍频,而且还能对电子转移速率有一定的调制作用.21,22为了更深入地研究影响电子转移速率的因素,激发态振动能级间的相干振动效应必然成为人们研究的热点.当研究者采用飞秒激光研究染料敏化TiO2纳晶体系时,必然会在染料激发态的各个振动能级间形成相干振动波包,若仍使用飞秒激光脉冲作为探测脉冲,则能实时地研究染料敏化TiO2纳晶体系界面间的超快光致各向异性电子转移动力学过程.
本文基于泵浦-探测(pump-probe)光谱技术的理论,采用文献20提出的有关激发态振动能级间的相干振动效应对电子转移速率影响的理论,结合Frank-Condon因子的唯象公式从理论上研究不同的重组能、注入能级位置、初始振动波包对染料激发态电子占有率的影响,为今后进行光致电子转移速率的实验研究和染料敏化太阳能电池的应用研究提供理论基础和指导.
2 理论模型
2.1 染料激发态衰减动力学的理论基础
图1为基于泵浦-探测光谱技术研究染料敏化TiO2纳晶材料体系的超快光致电子转移过程的能级示意图,假定染料与TiO2纳晶材料之间主要通过键连相互作用形成电荷转移复合物.23,24在本文中采用两电子态(基态|g〉和激发态|e〉)来表征染料分子,其中电子激发态振动能级的有效量子数为{ν};CB、VB和ΔEgap=3.2 eV分别代表TiO2半导体的导带(其振动能级近似为准连续带,有效量子数为{μ})、价带和能隙宽度;KET和KBET分别表示电子从染料电子激发态到半导体导带振动态的光致电子转移速率常数和由半导体导带振动态转移到染料电子基态的逆向电子转移速率常数;S0、S*和S+分别表示染料分子处于基态、激发态和离子化态的存在形式;常数a表示有限宽半导体导带的半宽值,b表示电子注入能级位置,即从染料激发态振动能级到半导体导带底的距离;初始振动波包是指超短激光脉冲在染料激发态振动能级间所形成的相干叠加,它随着激发脉冲的脉宽或者波长的变化而变化.如图1所示,当选择适当波长的光激发该体系时,吸附在TiO2纳米粒子表面上的染料分子被激发到激发态(过程I),电子通过染料激发态注入到TiO2纳米粒子的导带(过程II),未发生电子转移的染料分子通过发射荧光回到基态(过程V).然而,对于染料与TiO2所形成的电荷转移复合物,7光激发会形成电荷分离,使电子直接从电荷转移复合物注入到TiO2纳米粒子的导带(过程IV);TiO2导带的电子与染料分子阳离子复合时产生电荷转移发光(过程III).注入到TiO2导带中的电子可经历表面态捕获或在导带内经历弛豫和失相过程,最后与染料阳离子发生复合反应,即逆向电子转移.电荷转移发光和复合反应两个过程都可归为逆向电子转移.23,25图1中traps为电子捕获态.
假设激发脉冲为超短脉冲,可以忽略染料分子电子基态的电子转移问题,从而认为在超快光致电子转移过程中,电子转移的初始态|φe〉是由激发脉冲在染料分子势能曲面上的振动能级间构建粒子数相干(振动波包)的染料分子的电子激发态;显然,电子转移的终态|φk〉由离子化分子(产物态)的电子-振动准连续态(electronic-vibronic quasicontinnum)组成.20因此,体系的Hamiltonian量(H)可表示为:


图1 染料敏化TiO2纳晶体系的有限电子-振动准连续能级示意图Fig.1 Scheme of energy levels of finite electronicvibrational quasicontinuum for dye-sensitized TiO2 nanocrystalline system|g〉:electronic state of ground-state;|e〉:electronic state of excitedstated;ν:vibrational quantum numbers;20μ:effective quantum numbers corresponding to finite electronic vibronic quasicontinuum;20 CB:conduction band;VB:valence band;ΔEgap:energy gap; KET:electron transfer rate constant;KBET:back electron transfer rate constant;S0:ground state;S*:excited state;S+:charge separation state; traps:trap states;a:half width of a finite conduction band; b:position of the injecting level;I:photoexcitation process(pump); II:electron transfer;III:charge transfer emission;IV:photoexcitation of chargetransfercomplex;V:fluorescence;redGaussian shape:initial vibrationalwavepacket;recom.:recombination;fluo:fluorescence
其中,Hm(m=e,k)为各个电子态的Hamiltonian量,He和Hk分别表示染料激发态能级电子态的Hamiltonian量和半导体导带能级电子态的Hamiltonian量;Ve,k=〈φe|H|φk〉为染料激发态能级和半导体导带能级间的电子跃迁矩阵元(电子耦合常数);H为染料敏化TiO2半导体体系的总Hamiltonian量.20
假设电子在振动能级上的运动近似为简谐振动,则激发态和导带电子态的Hamiltonian量Hm可表示为:20

Hm的振动本征波函数近似为多个单振动模的振动波函数的乘积因此,Hm的能量本征值也可表示为:20

其中,εe和εk分别为电子在染料激发态和导带的电子态的振动基态的振动频率为与各个振动模对应的振动量子数,ωv为与各个振动量子数相对应的振动频率,ωξ为染料激发态相邻振动能级间的振动频率差.
由染料激发态和TiO2半导体导带所组成体系的电子-振动波函数可以表示为:20

其中,εev和εkμ分别表示电子在染料激发态振动能级上的振动频率和电子在半导体导带振动能级上的振动频率,Aev(t)和Akμ(t)分别表示电子出现在染料激发态振动能级上的波函数的振幅和电子出现在半导体导带振动能级上的波函数的振幅.我们假设电子出现在染料激发态某一确定振动能级上的波函数振幅的零级解满足e指数衰减:20

且染料激发态与导带界面间的振动跃迁满足能量守恒:20

由文献20可知,染料激发态不同振动波函数对初始振动波包的贡献遵守泊松分布,可由参数gp表示为:

其中,gp与染料激发态和基态势能曲面之间的无量纲位移有关,且随着gp的增加,泊松分布的平均值向激发态较高能量的振动态移动.因此,我们可以通过gp描述初始振动波包对光致电子转移速率常数的影响,它是研究体系中的一个极为重要的系统参数.已知,光致电子转移的速率常数满足:20

求解体系时间相关的薛定谔方程:

我们可以得到电子出现在染料激发态上的占有率为:20

其中,激发态振动能级电子转移的速率常数为:

式(10)中右边第一个求和项代表了激发态各个振动能级没有振动相干效应时激发态电子的直接衰减,而第二个求和项代表了激发态各个振动能级相干振动效应导致的激发态电子衰减;并且式(11)中每一个Frank-Condon因子都代表有机染料激发态振动能级与半导体导带振动能级间电子-振动跃迁,且(2κ)-1=80 fs.因此,式(10)是描述超快光致各向异性电子转移到半导体导带时染料激发态衰减动力学的一般表达式;当注入电子的能级距离导带底的能量差值远远大于重组能值(b>>λ)时,则式(10)中的相干项消失,这就是所谓的宽带条件.
综上所述,由激发态电子占有率的表达式可知,相干效应的调制作用是通过振动波函数的重叠因子即Frank-Condon因子体现的,而决定具有初始振动相干效应的染料激发态衰减动力学的主要因素有:有限宽半导体导带、重组能和电子耦合强度、电子注入能级的位置、激发态中不同的初始振动波包.
2.2 Frank-Condon因子唯象公式建立的基础
上文通过理论分析和推导,得出了激发态电子布居随时间的演化关系(即式(10)),我们假设:电子出现在染料激发态振动能级上的波函数和电子出现在半导体导带振动能级上的波函数间的Frank-Condon因子服从一种类似泊松分布关系,并且这种分布关系可表示为:

其中,e指数项中的第一项是重组能对Frank-Condon因子的影响参数,第二项为注入能级位置对Frank-Condon因子的影响参数,第三项为初始振动波包对Frank-Condon因子的影响参数.只要激发态振动能级间隔和电子所处的振动能级位置确定后,唯象公式中A、B和C的参数也就确定了,而且A和B两个参数为定常数,它们和外界因素没有关系.
Frank-Condon因子唯象公式的建立是依据以下三个条件提出来的.
首先,染料激发态振动能级振动波函数与基态振动能级振动波函数间的Frank-Condon因子满足泊松分布:20
其次,在研究染料敏化半导体材料界面间的光致电子转移过程中把分子振动能级的振动形式看成是一种简谐振动,而简谐振动的本征波函数可表示为:26-29
第三,由文献20可知,当注入能级位置处于导带中间位置时,电子转移速率最大,随着注入能级位置移向导带上下边缘,电子转移速率变小.
3 结果与讨论
基于2.2节的三个条件,并结合式(10)、(11)和 (12)考虑在不同重组能、注入能级位置、初始振动波包的条件下,研究激发态电子占有率随时间的演化关系;再与相同条件下由式(10)和(11)所得激发态电子占有率随时间的演化关系进行比较;最终分析唯象Frank-Condon因子式的合理性.为了研究激发态振动能级间的相干振动对电子转移速率的影响,设TiO2纳晶半导体导带宽为1.4 eV,即唯象公式中a取0.7 eV,16并设注入能级距离导带底位置的能量差值为b;取染料单模振动频率为0.2 eV和N=11个第一激发态振动能级;基于这些参数,利用激发态电子占有率表达式和唯象公式式进行计算,分别研究重组能、注入能级位置、初始振动波包对激发态电子占有率的影响.
3.1 重组能对电子转移速率的影响
由重组能λ表达式可知,电子转移前后分子原子核几何构型的变化能够引起重组能的改变,当注入能级位置不发生变化时,也就是发生电子转移的电子所处的振动能级位置不发生变化的情况下,原子核几何构型的变化是通过改变电子出现在激发态振动能级上的几率波振幅来实现.因此,重组能的改变将会导致原子核几何构型的变化和电子出现在激发态振动能级上的几率波振幅的变化,即通过调节这两个参数实现不同重组能对电子转移速率影响的研究.由图2可知:随着重组能的增加,电子转移速率变慢,并且激发态振动能级间的相干振动效应更加明显.
电子转移前后染料分子几何构型的变化对电子转移速率有着重要的影响.由于当注入能级位置一定时,电子所处的振动能级的振动频率也是一定的,那么由重组能λ的表达式可知,当电子振动频率一定时,重组能越大,电子转移前后发生的核几何构型的变化就越大,从而重组能λ的两个无量纲位移的差值就会越大,导致唯象公式中e指数项中的第一项变大,进而导致Frank-Condon因子变小,最终影响电子在激发态振动能级上的占有率将变大;因此,发生光致电子转移的电子数量变小,体现在速率上即为电子转移速率变小.
电子出现在激发态振动能级上的几率振幅对激发态电子占有率有着极为重要的影响.当电子注入能级位置不变时,随着重组能的增加,原子核几何构型将会随着增加,通过前面的分析可知,这种原子核几何构型的增加是通过增加电子出现在激发态振动能级上的几率振幅来获得的,因此,重组能的增加必然导致电子出现在激发态振动能级上的几率振幅的增加,通过激发态电子占有率的具体表达式(式(10))和唯象公式(式(12))计算所得的曲线(见图2)可知,激发态振动能级电子出现几率振幅的增加将会导致激发态振动能级间相干振动对电子转移速率调制作用的增强,也就是由相干振动引起的节拍变得更加明显.这与文献20中提到的情况相一致,从而验证了唯象公式式中Frank-Condon因子服从类似泊松分布关系的合理性,进一步说明了唯象公式式(12)的合理性.
3.2 注入能级位置对电子转移速率的影响
由染料能级和半导体能带结构图1可知,注入能级位置的改变必然引起导带振动能级有效振动量子数μ的改变,而通过重组能λ的表达式可知,当保持激发态电子占有率不变时,导带振动能级有效振动量子数μ的改变,这必将会引起重组能的变化;若要保持重组能不变,则可以通过调节激发态电子占有率来实现,而对激发态电子占有率的调节又是通过对电子出现在激发态振动能级上的振幅来实现.因此,通过改变注入能级相对于半导体导带边缘的位置和电子出现在激发态振动能级上的振幅这两个参数可以研究激发态电子占有率随时间的变化与注入能级位置改变之间的关联.如图3所示,注入能级位置由导带中间向导带底边缘移动时,电子转移速率变小,且激发态振动能级间的相干振动作用增强.
首先,当注入能级位置由导带中间向导带底边缘移动时,Frank-Condon因子(χev|χiμ)将变小,导致电子转移速率变小.
其次,在重组能不变的情况下,当注入能级位置从导带中间位置移向导带底边缘时,染料激发态各个振动能级上电子占有率也是随着增大,也就是电子出现在激发态振动能级上的几率振幅也会随之变大.这是因为,由能量守恒表达式可知,当注入能级移位于导带中央时,与Frank-Condon因子相关的导带振动能级的有效振动量子数μ就越大,从而对所有相关Frank-Condon因子的求和就会趋于1,最终导致电子转移速率变大,激发态振动能级间的相干振动作用减弱,这就非常接近于导带的宽带宽条件.相反,当注入能级移向导带底边缘时,导带振动能级有效振动量子数μ会随之减小,从而对所有相关Frank-Condon因子的求和就会小于1,从而导致电子转移速率变小和激发态振动能级间的相干振动作用增强(如图3所示).另一方面,注入能级移向导带顶边缘与注入能级移向导带底边缘是两种完全相反的情形.

图2 重组能对染料分子激发态时间相关占有率的影响Fig.2 Effect of reorganization energies on the time dependent occupation probability of the excited state of dye moleculePe(t):time dependent occupation probability;λ:reorganization energy;b:energy corresponding to the position of injecting level
通过对改变注入能级位置对电子转移速率影响的分析,所得结论与文献20中提到的情况相一致,从而验证了关于电子在激发态振动能级上的振动波函数和电子在导带振动能级上的振动波函数的Frank-Condon因子的唯象公式式(12)的合理性.
3.3 初始振动波包对电子转移速率的影响

图3 注入能级位置对分子激发态时间相关占有率的影响Fig.3 Effect of position of the injecting level on the time dependent occupation probability of the excited state of dye molecule
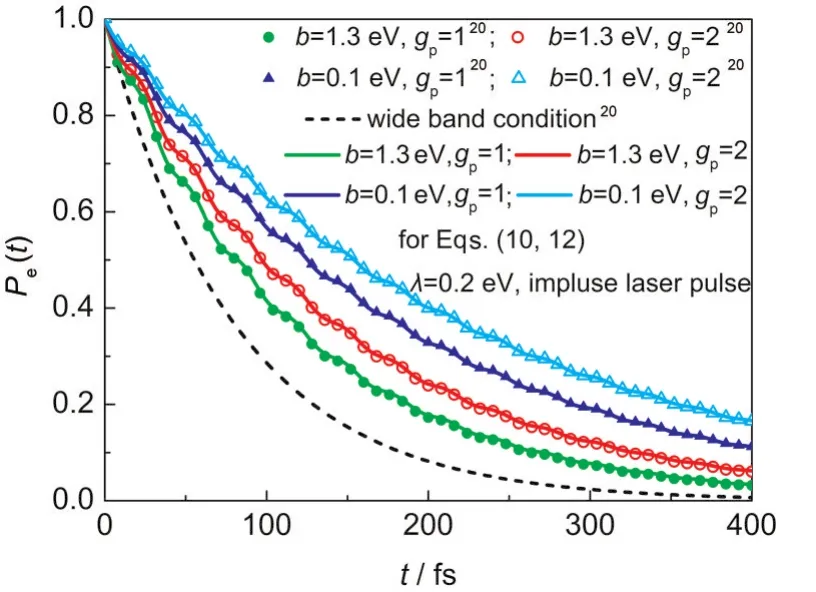
图4 初始振动波包对染料分子激发态时间相关占有率的影响Fig.4 Effect of initial vibrational wave packets on the time dependent occupation probability of the excited state of dye moleculegp:Poisson distribution of probabilities among the vibronic levels20
图4所示为注入能级分别位于导带底和顶时,初始振动波包的变化对光致电子速率的影响.很明显,当注入能级位于导带底时,初始振动波包处于较高振动能级时的电子转移比初始振动波包处于较低振动能级时电子转移快,这是由于当注入能级位于导带底时,电子处于较高振动能级(如gp=2)时的Frank-Condon因子(χev|χiμ)的值比电子处于较低振动能级时的Frank-Condon因子值大,因此电子处于较高振动能级时的电子转移比电子处于较低振动能级(即gp=1)时的电子转移容易发生.当注入能级位于导带顶时,处于较低振动能级的电子转移比处于较高振动能级的电子转移快,这是由于当注入能级位于导带顶时,电子处于较低振动能级(即gp= 1)时的Frank-Condon因子(χev|χiμ)比电子处于较高振动能级时的Frank-Condon因子大,因此电子处于较低振动能级时的电子转移比电子处于较高振动能级(即gp=2)时的电子转移容易发生.

图5 重组能量和注入能级位置对染料分子激发态时间相关占有率的影响及理论计算与实验数据的比较Fig.5 Effectof the reorganizationenergyand position of the injectinglevelenergyon the timedependent occupation probabilityof the excitedstate of dyemoleculeand the comparisonbetween theoreticalcalculationand experimentaldataThe conduction band width of TiO2nanocrystalline semiconductor is 2.0 eV.
因此,电子所处的染料激发态振动能级位置的变化将会导致初始振动波包的变化,而又将会引起半导体导带有效振动量子数μ的取值范围的变化,因此,可以认为初始振动波包的变化将会导致半导体导带有效振动量子数μ的取值范围的变化,从而引起Frank-Condon因子(χev|χiμ)的大小变化,进而影响了界面间电子转移速率的大小.在唯象公式中,通过改变参数C来实现初始振动波包对电子转移速率的影响.
3.4 Frank-Condon因子唯象公式中参数的确定
通过以上结合唯象公式研究了在不同重组能、注入能级位置、初即振动波包的条件下,激发态电子占有率随时间的演化关系,得出了唯象公式式(12)中各项参数的具体系数,修正后的唯象公式式(12)可以表示为:

其中A=16,B=0.4735,C=0.1.
3.5 Frank-Condon因子唯象公式在二萘嵌苯敏化TiO2纳晶体系中的应用
为了进一步说明Frank-Condon因子唯象公式分析实验数据之间的合理性,选择二萘嵌苯染料分子键连TiO2纳晶体系为研究对象.13本节中的单模振动频率为0.1 eV的染料激发态振动能级,由于最初振动能级间隔发生了变化必然导致注入能级位置和最初振动波包对Frank-Condon因子的影响,因此,在Frank-Condon因子中体现出B和C的变化,并且通过与文献13数据的比较可以确定B=0.4075和C=0.45.如图5所示为二萘嵌苯敏化TiO2纳晶体系(TiO2纳晶半导体导带宽为2.0 eV)在不同的重组能量和不同的注入能级位置对电子转移速率的影响.随着重组能量的增加电子转移速率减小,并且激发态振动能级间的振动效应增强;随着注入能级由导带中间移向导带边缘时,电子转移速率减小,同样激发态振动能级间的振动效应增强.因此,理论计算和实验数据13的比较基本吻合,从而有效地证明了唯象公式的合理性.
4 结论
在激发态电子占有率表达式和Frank-Condon因子唯象公式的基础上,从理论上研究了染料敏化TiO2纳晶系统中不同重组能、注入能级位置、初始振动波包条件下激发态振动能级间振动相干效应对光致电子转移速率的影响,并与文献中的研究结果进行了对比,证实了唯象公式的合理性,并获得了唯象公式的相关修正参数.通过分析可得如下结论:第一,随着重组能的增加,电子转移速率变小,并且激发态振动能级间的相干振动作用增强;第二,随着注入能级位置由导带中间移向导带边缘,电子转移速率变小,并且激发态振动能级间的相干振动作用增强;第三,得出了当注入能级位于导带底时,处于较高振动能级上的电子比处于较低振动能级上的电子转移速率快,而当注入能级位于导带顶时,情况正好相反.本文的工作将为今后进行光致电子转移速率的实验研究和染料敏化太阳能电池的应用研究提供理论基础和指导.
(1) Hagfeldt,A.;Gratzel,M.Chem.Rev.1995,95,49.doi:10.1021/ cr00033a003
(2) Kamat,P.V.Chem.Rev.1993,93,267.doi:10.1021/ cr00017a013
(3) Nozik,A.J.;Memming,R.J.Phys.Chem.1996,100,13061. doi:10.1021/jp953720e
(4) Zhao,G.J.;Han,K.L.Accounts Chem.Res.2012,45,404.doi: 10.1021/ar200135h
(5)Mao,M.;Wang,J.B.;Xiao,Z.F.;Dai,S.Y.;Song,Q.H.Dyes and Pigments 2012,94,224.doi:10.1016/j.dyepig.2012.01.011
(6) Gao,F.F.;Wang,Y.;Shi,D.;Zhang,J.;Wang,M.K.;Jing,X. Y.;Humphry-Baker,R.;Wang,P.;Zakeeruddin,S.M.;Grätzel, M.J.Am.Chem.Soc.2008,130,10720.doi:10.1021/ja801942j
(7)Jiang,L.L.;Song,Y.F.;Liu,W.L.;Yu,G.Y.;He,X.;Wang,Y.; Wu,H.L.;Yang,Y.Q.Acta Phys.Sin.2012,61,090505.[蒋礼林,宋云飞,刘伟龙,于国洋,何 兴,王 阳,吴红琳,杨延强.物理学报,2012,61,090505.]
(8) Nitzan,A.;Ratner,M.A.Science 2003,300,1384.doi:10.1126/ science.1081572
(9)Cheng,H.;Dong,J.Z.;Chao,H.;Yao,J.H.;Cao,Y.A.Acta Phys.-Chim.Sin.2012,28,850.[程 辉,董江舟,巢 晖,姚江宏,曹亚安.物理化学学报,2012,28,850.]doi:10.3866/ PKU.WHXB2012020111
(10) Hannappel,T.;Burfeindt,B.;Storck,W.;Willig,F.J.Phys. Chem.B 1997,101,6799.doi:10.1021/jp971581q
(11) Ramakrishna,S.;Willig,F.J.Phys.Chem.B 2000,104,68.doi: 10.1021/jp991428r
(12) Zimmermann,C.;Willig,F.;Ramakrishna,S.;Burfeindt,B.; Pettinger,B.;Eichberger,R.;Storck,W.J.Phys.Chem.B 2001, 105,9245.doi:10.1021/jp011106z
(13) Ramakrishna,S.;Willig,F.;May,V.;Knorr,A.J.Phys.Chem.B 2003,107,607.doi:10.1021/jp027104b
(14) Gundlach,L.;Felber,S.;Storck,W.;Galoppini,E.;Wei,Q.; Willig,F.Res.Chem.Intermed.2005,31,39.doi:10.1163/ 1568567053146841
(15) Persson,P.;Lundqvist,M.J.;Ernstorfer,R.;Goddard,W.A.; Willig,F.J.Chem.Theory Comput.2006,2,441.doi:10.1021/ ct050141x
(16) Jean,J.M.;Friesner,R.A.;Fleming,G.R.J.Chem.Phys.1992, 96,5827.doi:10.1063/1.462858
(17) Kühn,O.;May,V.;Schreiber,M.J.Chem.Phys.1994,101, 10404.doi:10.1063/1.467921
(18) Fuchs,C.;Schreiber,M.J.Chem.Phys.1996,105,1023.doi: 10.1063/1.471946
(19) Bixon,M.;Jortner,J.J.Chem.Phys.1997,107,1470.doi: 10.1063/1.474500
(20) Ramakrishna,S.;Willig,F.;May,V.J.Chem.Phys.2001,115, 2743.doi:10.1063/1.1386433
(21) Jean,J.M.J.Chem.Phys.1994,101,10464.doi:10.1063/ 1.467864
(22)Wynne,K.;Reid,G.D.;Hochstrasser,R.M.J.Chem.Phys. 1996,105,2287.doi:10.1063/1.472097
(23)Ramakrishna,G.;Ghosh,H.N.J.Phys.Chem.B 2001,105, 7000.doi:10.1021/jp011291g
(24) Lee,K.E.;Gomez,M.A.;Elouatik,S.;Demopoulos,G.P. Langmuir 2010,26,9575.doi:10.1021/la100137u
(25) Ghosh,H.N.J.Phys.Chem.B 1999,103,10382.doi:10.1021/ jp9918611
(26) Fujishima,A.Nature 1972,238,37.doi:10.1038/238037a0
(27) OʹRegan,B.;Grätzel,M.Nature 1991,353,737.doi:10.1038/ 353737a0
(28) Nazeeruddin,M.K.;Angelis,F.D.;Fantacci,S.;Selloni,A.; Viscardi,G.;Liska,P.;Ito,S.;Takeru,B.;Grätzel,M.J.Am. Chem.Soc.2005,127,16835.doi:10.1021/ja052467l
(29) Ramakrishna,S.;Willig,F.;May,V.Chem.Phys.Lett.2002, 351,242.doi:10.1016/S0009-2614(01)01376-8