冲压发动机导弹爬升轨迹与推力调节规律优化

尚腾，谷良贤，赵吉松，龚春林

(西北工业大学航天学院，陕西西安 710072)

引言

冲压发动机导弹的弹道设计不同于固体火箭发动机导弹的弹道设计，主要体现在冲压发动机推力与弹道的强耦合性。一方面，冲压发动机的内部参数和性能指标随导弹的飞行速度、飞行高度、攻角及实际进入发动机的空气流量而变化;另一方面，冲压发动机的比冲及推力直接影响导弹的质量和飞行性能。所以，在设计以冲压发动机为动力的导弹弹道时必须考虑推力调节规律的设计［1］。冲压发动机的推力调节多采用控制余气系数的方法，其特点是实现方便且有利于保证冲压发动机燃烧的稳定性［2］。

以冲压发动机为动力的超声速、中远程战术导弹，通常用助推器将导弹加速到达预定的高度和速度，冲压发动机再接力工作，将导弹加速到规定的巡航速度和巡航高度进行巡航飞行。爬升弹道的设计优化需要解决如何最优地使导弹从接力点(冲压发动机开始工作)爬升到巡航状态。文献［3-4］在进行冲压发动机导弹爬升弹道优化的研究中，余气系数只根据导弹飞行马赫数进行了适当调节，并没有参与优化。而冲压发动机导弹爬升过程中飞行速度、高度、导弹姿态等均在较大范围内变化，只有把冲压发动机的推力调节规律和导弹弹道设计协调起来，进行一体化优化设计，才能获得合理的结果。

直接法对目标函数的解析性质不作苛刻要求，且适合各种精度的弹道模型，本文采用直接法求解冲压发动机导弹爬升这一最优控制问题，建立了爬升轨迹与推力调节规律共同参与优化的一体化优化设计模型。为了克服直接法对初始点选取敏感，容易收敛到局部最优解的缺点，将粒子群算法(PSO)与变尺度算法(BFGS)串联结合，寻优前期利用PSO较强的全局搜索能力，搜索至全局最优点附近;寻优后半阶段利用BFGS较强的局部寻优能力，以提高搜索精度。设计结果表明，本文提出的爬升弹道一体化设计方法能够成功地求解冲压发动机爬升弹道问题，具有较好的工程应用价值。

1 数学模型

1.1 爬升弹道运动模型

将导弹看作可控质点，导弹在铅垂平面内的运动方程组为:

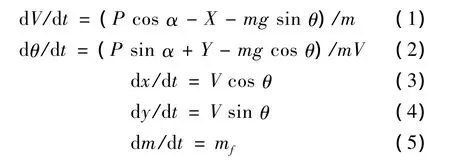
式中，V为导弹速度;P为推力;m为导弹质量;X为阻力;Y为升力;α，θ分别为攻角和弹道倾角;x为纵向射程;y为高度;mf为发动机燃料消耗率。

设冲压发动机导弹的爬升弹道光滑且二阶连续，则可用三次样条曲线插值拟合其爬升轨迹。下面推导导弹按照预设飞行轨迹y*(x)飞行时的需用攻角。

由式(3)、式(4)可得:

给定导弹爬升飞行的预设飞行轨迹y*(x)，则可以利用式(6)～式(9)求出按此轨迹飞行时的需用攻角。

对式(1)～式(5)进行积分求解，飞行攻角取需用攻角，即可得到导弹的实际飞行弹道y(x)。其中，冲压发动机的性能随导弹的飞行速度、飞行高度、迎角及实际进入发动机的空气流量而变化。

1.2 冲压发动机推力模型及推力调节规律

冲压发动机的推力计算公式为:

式中，ma为空气流量;ve为发动机喷口气流速度;v为飞行器速度;pe为喷口压强;pa为环境压强;αf为余气系数，αf=ma/(Lmf);L为单位燃料消耗的理论空气量。

以某头部进气冲压发动机为例，采用一元流理论，得到冲压发动机的推力、燃料秒流量随飞行高度、马赫数、攻角及余气系数的变化关系［2］，即:

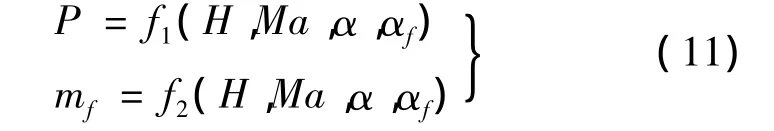
式中，f1，f2以插值表的形式给出。发动机的推力调节就是通过调节供油量，控制余气系数按照所需的规律进行变化。

2 优化问题表达与优化算法

2.1 优化问题描述

以冲压发动机为动力的导弹爬升段设计优化的目标是使导弹达到巡航高度并以巡航马赫数飞行，且要求燃料消耗量少，飞行时间短。时间最短和燃料最省是两个相互矛盾的弹道优化目标［4］，本文研究燃料最省的情况。

弹道优化的初始条件是给定的接力点位置、接力马赫数;终端约束为给定的巡航高度、弹道倾角(0°)、最小巡航马赫数;在导弹爬升过程中有最大攻角的限制。弹道优化的目标函数和约束条件的数学描述为:

式中，ycruise，Mamin为给定的巡航高度和最小巡航马赫数。

2.2 弹道样条离散

在三次样条曲线中，两个节点之间的曲线由三次多项式拟合生成，整个样条曲线由各段三次多项式曲线组成，相邻两段在节点处二阶连续。本文构造三次样条时采用自然边界条件，即两端点处的二阶导数为零。采用三次样条插值方法可以对弹道优化这一最优控制问题进行离散并参数化［5-6］。

将弹道沿射程x分为n段，形成n+1个节点［x0，x1，…，xn］，优化变量为各节点处的飞行轨迹纵坐标yi和余气系数αfi(i=0，1，…，n)。通过样条插值，可构建出导弹在竖直平面内的轨迹y*(x)和余气系数变化规律α*f(x)。

2.3 PSO-BFGS串联优化方法

PSO算法有着较强的全局搜索能力，但局部搜索能力较差，搜索精度不够高［7］。BFGS变尺度法是求解无约束优化问题最有效的算法之一，搜索精度较高，数值稳定性好。结合两者优点，将PSO算法与BFGS算法串联形成PSO-BFGS优化算法。

PSO算法首先在可行解空间和速度空间随机初始化粒子群(Particle Swarm)，即确定粒子(Particle)的初始位置和初始速度。其中，位置用于表征问题解。设d维搜索空间中的第i个粒子的位置和速度分别表示为 xi= ［xi，1，xi，2，…，xi，d］和 vi= ［vi，1，vi，2，…，vi，d］。通过评价各粒子的适应度值，确定每个粒子所经 过 的最佳位置 pi= ［pi，1，pi，2，…，pi，d］，以及群体所发现的最佳位置 pg= ［pg，1，pg，2，…，pg，d］，再按下式更新各粒子的速度和位置:

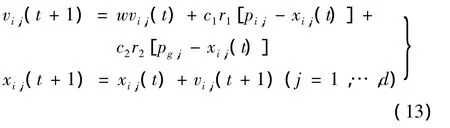
式中，w为惯性权重因子;c1和c2为正的加速常数;r1和r2为在0～1之间均匀分布的随机数。

设粒子的速度区间为［vmin，j，vmax，j］，位置范围为［xmin，j，xmax，j］，当粒子速度超出限制时取边界值。位置超出范围时，按下式确定［8］:

式中，f为弹性因子(0≤ f≤1)，表示粒子在超出边界时，被弹回到可行解空间内的强弱程度。采用此式有利于求解最优解在边界附近的问题。

BFGS的基本思想为［8］:迭代过程中，在 x(k+1)处按下式生成对称正定矩阵Hk+1，以代替海森矩阵的逆阵:

式中，g(k)=▽ f(x(k))，由中心差分格式给出;Δg(k)=g(k+1)－ g(k);Δx(k)=x(k+1)－ x(k)。然后，以p(k+1)= －Hk+1g(k+1)为x(k+1)处的搜索方向进行搜索。BFGS对一维搜索算法精度要求较高，文中采用三次曲线拟合法［8］。

PSO-BFGS串联混合算法的优化流程如图1所示。

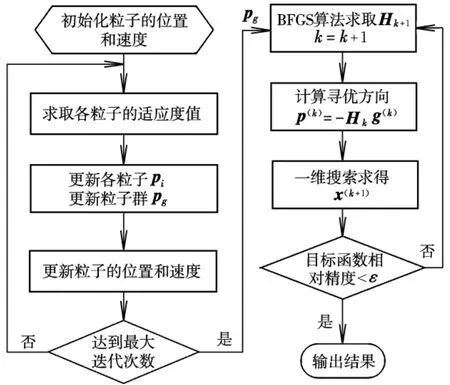
图1 PSO-BFGS算法流程图

针对爬升弹道的末端约束，通过在适应度函数中增加惩罚函数来处理。适应度函数选为:

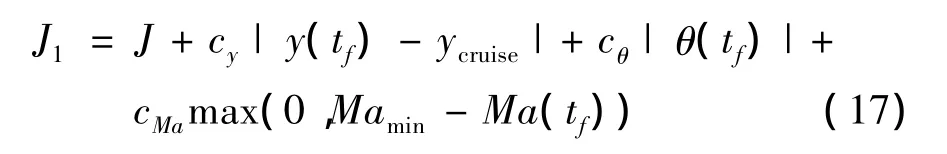
式中，cy，cθ，cMa分别为终端高度、弹道倾角和速度的惩罚系数。则爬升弹道优化问题转换为无约束优化问题，可由PSO-BFGS混合算法寻优求解。

3 设计实例

采用上述弹道优化方法对冲压发动机导弹的爬升弹道进行优化。算例设计参考了文献［1］和文献［3］，主要计算条件为:接力点马赫数2.2，接力点高度2 km，巡航高度15 km，终点弹道倾角0°，终点马赫数大于2.4，爬升终点距接力点的水平距离为25 km。为了观察轨迹与推力调节一体化设计在节省燃料方面的贡献，本文对以下两种方案进行了优化。

方案1:仅爬升轨迹参与弹道优化，余气系数变化规律预先设定为:

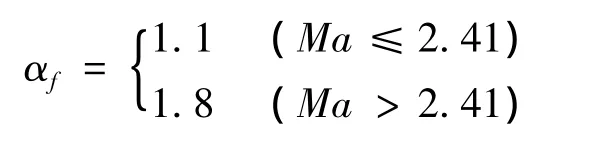
此方案类似文献［3-4］中采用的方案。

方案2:爬升轨迹和余气系数都参与弹道优化，即前文提出的一体化设计方案。

方案1中，弹道采用6个节点作为控制点，沿x向均匀分布，y1取 2 000.0，y2～ y5∈［2 000.0，15 000.0］，y6∈［14 500.0，15 500.0］。方案 2 中，弹道离散同方案1，余气系数离散控制点也取6个，沿 x向均匀分布，αf1取0.9，αf2～ αf6∈［0.9，2.0］。方案2的优化问题规模是方案1的2倍，图2给出了方案2的求解收敛过程。可以看出，PSO寻优前期，适应度值(J1)迅速下降，更新n=40代以后，适应度值就无明显改进，收敛至37.536 0;BFGS方法经过23次迭代，收敛至35.149 7，较PSO算法的优化结果提高6.36%。优化求解得到的两种方案的爬升轨迹和飞行参数见图3～图6。

图2 方案2的求解收敛过程

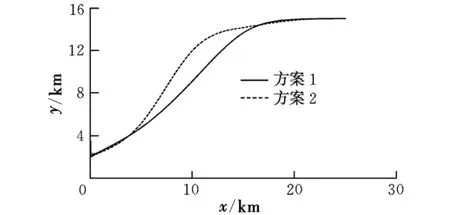
图3 两种方案最优爬升弹道

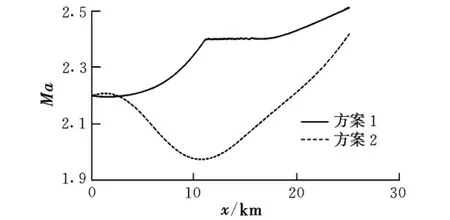
图4 爬升中马赫数变化

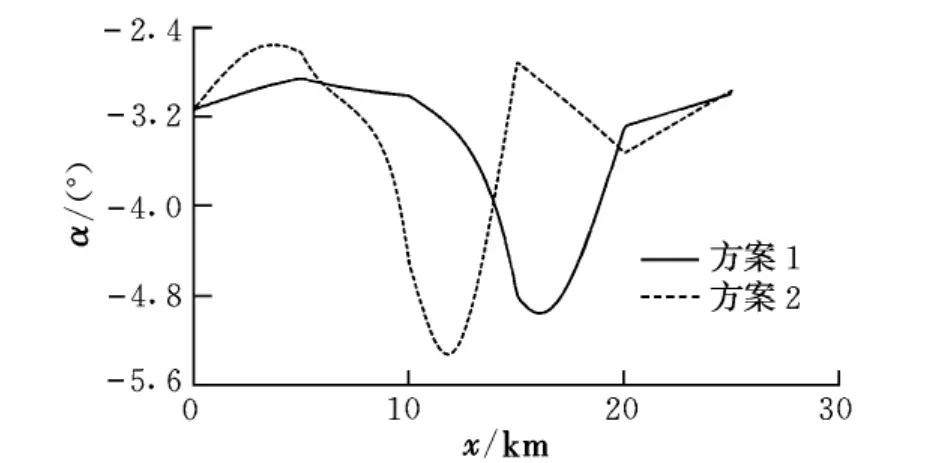
图5 爬升中攻角变化

图6 爬升中推力变化

图6方案1曲线中点划线表示:推力值在导弹飞行马赫数接近2.41时出现震荡。两种方案爬升飞行的末端参数及飞行过程中的攻角绝对值的最大值见表1。

表1 两种方案的优化结果比较

仿真结果显示，两种设计方案的设计结果均达到了设计要求。方案2中，爬升过程总消耗燃料量为35.149 3 kg，比方案 1 减少 5.102 4 kg，减少了12.68%，爬升时间增加5.0 s。燃料消耗的减少对于减少导弹发射质量或增加导弹的射程是十分有意义的，且接力爬升段在冲压发动机的整个飞行过程中所占比例较小，爬升段时间的少量增加是可以接受的。

对比两种方案下的爬升弹道:在爬升前半段，方案1中导弹作加速爬升飞行，速度已达到末端速度要求;方案2通过优化余气系数，使导弹作减速爬升飞行。在爬升后半段，方案1中，导弹速度略有增加;而方案2中，导弹呈加速飞行状态，由于导弹已经接近平飞高度，加速效率高。可见，采用方案2，导弹以较小的平均飞行速度完成爬升过程，可以实现节省燃料，进而达到减小导弹发射质量或增加射程的目的。

4 结束语

本文采用直接法建立了飞行轨迹形状和推力调节规律共同参与优化的冲压发动机导弹的爬升弹道一体化优化模型，并采用PSO-BFGS混合算法进行求解。优化结果表明:采用样条插值直接离散方法和PSO-BFGS混合算法能够较好地求解冲压发动机导弹爬升弹道优化问题。在冲压发动机导弹爬升弹道设计优化中，推力调节规律与爬升轨迹一体化优化设计，可获得先减速再加速的爬升方案，采用此方案，导弹能以较小的平均速度完成爬升过程，可以显著节省燃料，提高导弹性能。

［1］ 刘恒军，沙建科，王华.冲压发动机导弹弹道多目标优化［J］.系统仿真学报，2009，21(9):2764-2766.

［2］ 刘兴洲，于守志.飞航导弹动力装置(上)［M］.北京:宇航出版社，1992.

［3］ 王华，杨存富，刘恒军.冲压发动机为动力导弹爬升弹道优化［J］.弹箭与制导学报，2008，28(3):185-188.

［4］ 王华，杨存富，刘恒军.以冲压发动机为动力的导弹爬升弹道研究［J］.现代防御技术，2008，36(4):27-30.

［5］ 陈胜琪.基于样条曲线的机动弹头再入轨迹优化研究［J］.飞行力学，2009，27(1):63-65.

［6］ Ken Cote.Complex 3D flight trajectory generation and tracking using cubic splines［C］//AIAA’s 1st Technical Conference and Workshop on Unmanned Aerospace Vehicles.Portsmouth，USA，2002.

［7］ Rhonald M J，Roy J H.Hybrid particle swarm-pattern search optimizer for aerospace propulsion applications//46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Nashville，USA，2010.

［8］ 粟塔山.最优化计算原理与算法程序设计［M］.长沙:国防科技大学出版社，2001.