基于终端角度约束的滑模制导律设计

李志平，郭建国，周军

(西北工业大学精确制导与控制研究所，陕西西安 710072)

引言

比例导引律通常是工程最易实现的制导律，也是一种最优制导律，但是随着当前导弹技术的发展，它已经不能适应导弹制导发展的需求［1］。如对于空地导弹，要求它能够按照指定的角度攻击地面目标，给制导系统设计提出了新的需求。

对于具有终端角度约束的制导律设计问题，通常是基于最优控制的方法来完成设计［1-6］。最简单的情况是在垂直平面内利用线性二次型最优控制方法设计攻击匀速运动目标的制导律［1］，从而满足终端角度约束的条件。文献［2-3］分别基于线性二次型最优控制理论和最小值原理的方法推导出了两种形式的终端角度约束制导律，但这种最优控制的方法往往都依赖于剩余时间的估计。文献［4-5］不仅给出剩余时间估计方法，而且给出了终端角度约束最优制导律的闭环解的形式。

此外，非线性控制的方法也应用于这种特殊制导律的设计中。针对固定目标，文献［6］基于制导控制一体化的思想设计了变结构制导律。文献［7-8］分别采用H∞控制方法和Nussbaum-type增益技术，设计了两种自适应终端角度约束制导律。

为解决有终端角度约束条件制导问题，本文基于变结构控制方法，根据终端角度约束条件，提出一种新的非线性的滑动模态，设计了一种新的具有角度约束的鲁棒自适应非线性变结构末制导律，并利用Lyapunov稳定理论证明了在滑动模态区的有限时间可达性和稳定性。最后通过数字仿真证明了设计方法的有效性。

1 弹目相对运动学模型

考虑空地导弹和目标在末端三维相对运动学的关系，如图1所示的视线坐标系为末制导过程的参考坐标系。原点O位于导弹质心;Oxyz为惯性坐标系;Ox4y4z4为末制导开始的视线坐标系，其中Ox4轴与弹目视线重合，由导弹指向目标为正;Oy4轴位于纵向平面，向上为正;Oz4轴按右手法则来确定，且位于侧向平面内。设视线坐标系相对于惯性坐标系的转动角速度为Ω，那么惯性牵连坐标系可认为经过两次旋转后与视线坐标系重合，两次旋转的角速度大小分别为，，若惯性牵连坐标系与各轴对应的单位矢量分别为i，j，k，那么导目相对距离R二次求导可得:

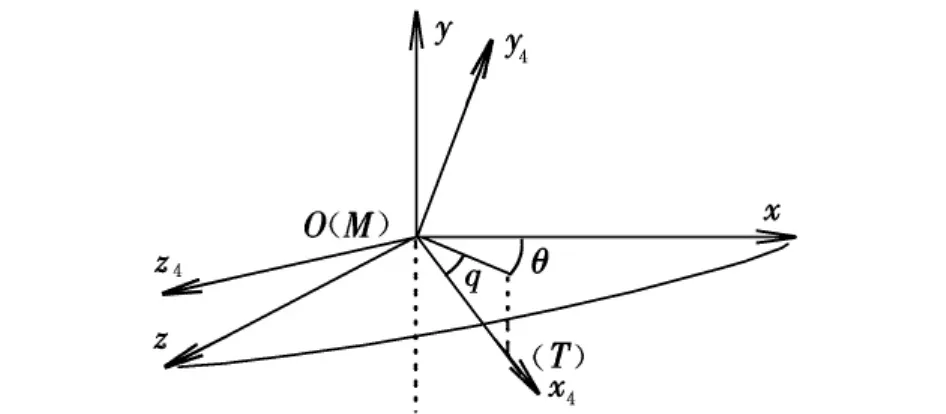
图1 弹目相对运动学关系

同时有:式中，a1=2;a(x)=cosqsinq;b=1/R;u=aM;aT=aty，设目标机动运动的加速度是有界的，即|aT|≤d。

2 非线性滑模制导律设计

2.1 末端角度约束问题

考虑到对命中目标有一定的终端角度约束，即要求在命中点处导弹的弹道倾角为期望的碰撞角度θf。假设qf为命中点处期望的视线角，且目标不机动情况下，有下列关系［9］:

显然，地面目标速度相对导弹速度较小，因此若忽略其速度，则由式(2)知，sin(θm－qf)≈0，故 θm≈qf，所以当qf= θf，则 θm≈θf，从而实现了终端角度的约束条件。

2.2 滑模制导律设计

针对纵向平面内弹目相对运动学模型(2)，利用变结构控制方法，设计一种新型的具有角度约束的制导律。

根据制导系统的设计原理，即准平行接近原理。在末制导段，期望弹目视线角速率在制导过程中趋向于零，即→0。同时考虑到qf=θf的条件，令x1m=qf，选取滑动模态s为:

式中，k＞0;0＜c1(t)d/R＜ε。则在有限时间内制导系统的弹目视线角速率为零，既保证了末制导系统的稳定性，也实现了终端角度x1m的约束。

证明:

(1)有限时间的可达性:

对滑动模态s求一次导，得:限时间内达到终端视线角x1m，同时也实现了x2=0的要求;当e(t)=0，即x1(t)=x1m时，可求出有限到达时间为:

由以上证明知，系统状态在控制律式(4)的作用下在有限时间内进入选定滑动区域，并在有限时间内到达理想的终端视线角，式(4)为导弹在纵向平面的制导指令。

注意:

(1)在末制导过程中，a(x)的值较小时，变结构对系统参数摄动有鲁棒性，同时考虑到抖振问题，故将式(4)变为:

(2)制导指令式(4)、式(5)也是由比例导引项和非线性补偿项组成，这样它的形式同一般的变结构导引律的形式相同。

(3)当终端角度x1m=0，可认为是无终端角度的要求时，式(5)变为:

特别地，当c1(t)=c1，c2(t)=c2，m=n=1 时，即为常规变结构控制方法中的线性滑动模态;而当c1(t)=R，c2(t)=0，k=k'||/R时，就为文献［10］设计的滑动模态和制导指令。

3 数字仿真与分析

下面通过数字仿真对本文所设计的具有终端角度约束的滑模制导律进行数字仿真验证。

考虑初始末制导的距离为5 km;导弹飞行马赫数为Ma=0.75;目标分别为固定目标和运动目标，运动速度为20 m/s;初始弹道倾角为0°;最大过载为6;非线性滑模制导律仿真参数为c1(t)=c2(t)=R，n=3，m=5;期望在命中时刻导弹的弹道倾角θf=－90°。仿真结果如图2～图4所示。

由图可知，对于固定目标，导弹飞行时间为22.14 s，命中点弹道倾角θ为－89.81°，最终视线角q为－89.9°，视线角速率保持在零值附近。

对于机动目标，导弹飞行时间为23.84 s，同样能够获得如图2～图4所示的弹道倾角、视线角以及视线角速率的变化趋势，命中点弹道倾角 θ为－85.49°，最终视线角q仍为 －89.9°，视线角速率仍保持在零值附近。相对于固定目标，弹道倾角与期望的－90°的角度有了一定的误差，主要原因是对于式(2)，当目标固定，则完全能得到θf=qf，而当目标在机动时，则有θf≈qf。所以目标的运动影响到命中点弹道倾角实现的精度。

图2 弹道倾角θ变化曲线

图3 视线角q变化曲线

图4视线角速率变化曲线

最后采用本文的制导律，固定目标时脱靶量为0.13m，目标运动时的脱靶量为0.04 m，从而保证了制导系统的精度。以上的仿真结果验证了所设计的非线性滑模制导律的有效性和适用性。

4 结论

本文利用期望弹道倾角和命中视线角的关系，设计了非线性滑模制导律，通过数学仿真，得到如下结论:基于准平行接近原理的思想，借助于控制命中点视线角的非线性变结构控制方法，可以较为有效地解决空地导弹具有终端角度约束的制导问题，便于带有复合制导系统的工程应用。

［1］ Kim M，Crider K V.Terminal guidance for impact attitude angle constrained flight trajectories［J］.IEEE Transactions on Aerospace and Electronic Systems，1973，9(6):675-683.

［2］ Song T L，Shin S J.Time-optimal impact angle control for vertical plane engagements［J］.IEEE Transaction on Aerospace and Electronic Systems，1999，35(2):738-742.

［3］ Song T L，Shin S J，Cho H J.Impact angle control for planar engagements［J］.IEEE Transaction on Aerospace and Electronic Systems，1999，35(4):1439-1444.

［4］ Ryoo C K，Cho H J，Tahk M J.Closed-form solutions of optimal guidance with terminal impact angle constraint［J］.IEEE Transaction on Aerospace and Electronic Systems，2003，39(2):504-509.

［5］ Ryoo CK，Cho H J，Tahk M J.Optimal guidance lawswith terminal impact angle constraint［J］.Journal of Guidance，Control，and Dynamics，2005，28(4):724-732.

［6］ Hou M Z，Duan G R.Integrated guidance and control of homingmissiles against ground fixed targets［J］.Chinese Journal of Aeronautics，2008，21(4):162-168.

［7］ 郭建国，周军.具有终端角度约束的H∞制导律设计［J］.火力与指挥控制，2009，34(12):44-46.

［8］ Guo JG，Zhou J.Guidance law design under impact angle constrain based on nussbaum-type gain technique［J］.Journal of China Ordnance，2010，6(4):253-257.

［9］ Byung SK，Jang G L.Homing guidance with terminal angular constraint against non-maneuve-ring and maneuvering target［R］.AIAA-97-3474，1997.

［10］ Zhou Di，Mu Chundi，Xu Wenli.Adaptive sliding-mode guidance of a homing missile［J］.Journal of Guidance，Control，and Dynamics，1999，22(4):589-594.