基于单调初等函数的缓冲算子构造

罗 党，孙玉玲，陈 玲

（华北水利水电学院，河南 郑州 450011）

灰色系统的特色是研究“小样本”与“贫信息”等不确定性问题，充分开发利用已占有的信息来挖掘系统本身固有的规律是灰色系统理论的基本准则．可以通过社会、经济、生态等系统的行为特征数据来寻求因素之间或自身的变化规律．灰色系统理论认为，尽管客观系统的表象复杂，数据离乱，但它们总有自身的整体功能，必然蕴藏某种内在的规律，关键是如何选择适当的方法来挖掘和利用它们．众多学者把缓冲算子的构造与函数联系起来，从而推广了缓冲算子的类型．文献［5］利用反函数定理构造了2类新强化缓冲算子;文献［6］构造了2类新弱化缓冲算子，并将其与党氏弱化缓冲算子进行比较，论证了党氏弱化缓冲算子为新算子的特例;文献［7］构造了2类新强化缓冲算子，并将其与谢氏强化缓冲算子进行比较，论证了谢氏强化缓冲算子为新算子的特例;文献［8］利用反函数定理，构造了4类新强化缓冲算子，并将其与关氏强化缓冲算子进行比较，论证了关氏强化缓冲算子为新算子的特例．笔者在他们工作的基础上，又构造出2大类基于初等函数的新缓冲算子，并研究其特性及其内在关系，从而使序列前一部分增长（减缓）速度过慢，而后一部分增长（衰减）速度过快的冲击扰动系统数据序列在建模预测过程中常常出现的定量预测结果与定性分析结论不符的问题得到了解决．

1 基本概念

定义1 设系统行为数据序列为X=（x（1），x（2），…，x（n）），若

3）若存在k，k'∈ {2，3，…，n}，有

称X为振荡序列．

定义2 设X为系统行为数据序列，D为作用于X的算子，X经算子D作用后所得数据序列记为

则称D为序列算子．称XD为一阶算子作用序列［1］．

序列算子的作用可以进行多次，相应地，若D1，D2，D3皆为序列算子，称D1D2为二阶算子，并称

为二阶算子作用序列．

同理称D1D2D3为三阶算子，并称

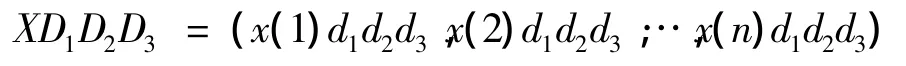
为三阶算子作用序列．

公理1 （不动点公理）设X为系统行为数据序列，D为序列算子，则D满足

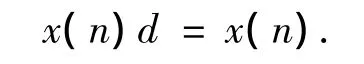
公理2 （信息充分利用公理）系统行为数据序列X中的每一个数据x（k），k=1，2，…，n都应充分地参与序列算子作用的整个过程．

公理3 （解析化、规范化公理）任意的x（k）d，（k=1，2，…，n），皆可由一个统一的x（1），x（2），…，x（n）的初等解析式表达．

满足上述3个公理的序列算子称为缓冲算子，XD称为缓冲序列［2］．

定义3 设X为系统行为数据序列，D为缓冲算子，当X分别为单调增长序列、单调衰减序列或振荡序列时：

1）若缓冲序列XD比原始行为数据序列X的增长速度（或衰减速度）减缓或振幅减小，则称缓冲算子D为弱化缓冲算子．

2）若缓冲序列XD比原始行为数据序列X的增长速度（或衰减速度）加快或振幅增大，则称缓冲算子D为强化缓冲算子．

缓冲算子具有以下性质［2］：

性质1 设X=（x（1），x（2），…，x（n））为系统行为数据序列，缓冲序列记为

性质2 设X=（x（1），x（2），…，x（n））为系统行为数据序列，缓冲序列记为

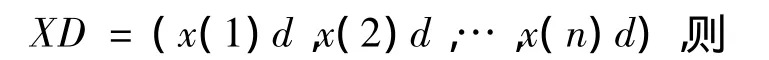
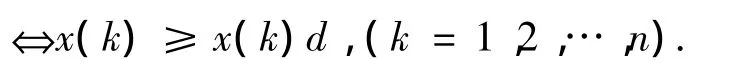
2）设X为单调衰减序列时，D为强化缓冲算子

2 缓冲算子的构造

2．1 强化缓冲算子的构造

定理1 设系统原始行为数据序列为x（k）＞0，令

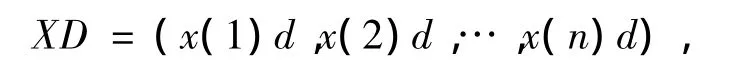
式中：x（k）d=f（x（k））eg（x（k））且f（x（n））=1，g（x（n））=lnx（n），f（x（k））关于x（k）单调递增，那么

1）当{x（k）}关于k单调递增，g（x（k））≤0时，D为强化缓冲算子．

2）当{x（k）}关于k单调递减，g（x（k））≥0时，D为强化缓冲算子．

证明：容易验证

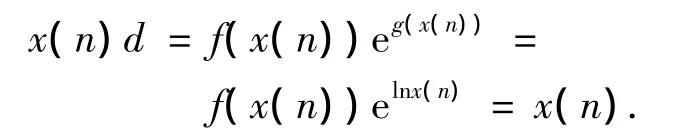
即D满足缓冲算子公理1．因而D为缓冲算子．

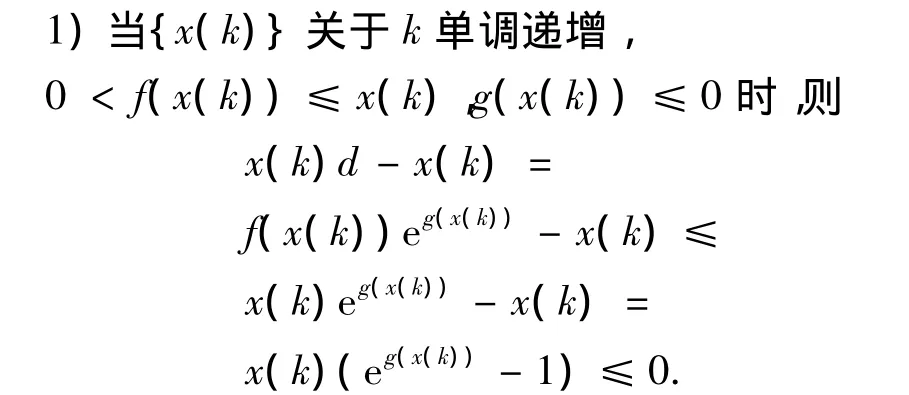
所以，x（k）d≤x（k），故D对单调增长序列为强化缓冲算子．

2）当{x（k）}关于k单调递减，

所以，x（k）d≥x（k），故D对单调递减序列为强化缓冲算子．

定理2 1）若g（x（k））关于x（k）单调递增，则定理1中的强化缓冲算子D对行为数据序列X作用后的序列算子其单调性不变．

2）若g（x（k））关于x（k）单调递减，则定理1中的强化缓冲算子D对行为数据序列X作用后的序列算子其单调性不变．

证明：1）当{x（k）}关于k单调递增，g（x（k））关于x（k）单调递增，g（x（k））≤0时，则

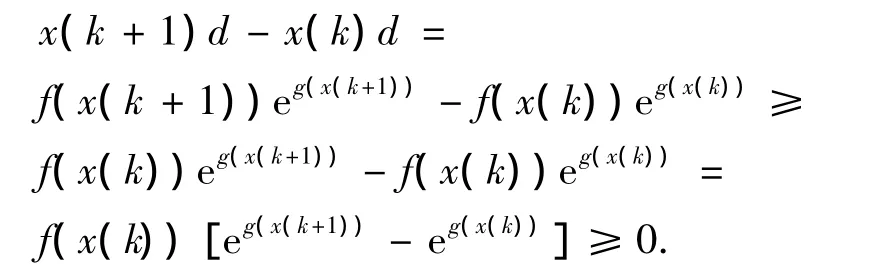
所以，x（k+1）d≥x（k）d，即XD关于k递增．

2）当{x（k）}关于k单调递减，g（x（k））关于x（k）单调递减，g（x（k））≥0时，则

所以，x（k+1）d≤x（k）d，即XD关于k递减．

2．2 弱化缓冲算子的构造

所以，x（k）d≤x（k），故D对单调递减序列为弱化缓冲算子．

定理4 定理3中的弱化缓冲算子D对行为数据序列X作用后的序列算子其单调性与X相反．

证明：1）当{x（k）}关于k单调递增，f（x（k）），g（x（k））关于x（k）单调递增，

证明：直接验证此处f（x（k）），g（x（k））满足定理3中条件即可．

3 应用实例

3．1 强化缓冲算子的应用

以文献［9］中的企业新产品1月至7月的月销售额（具体见表1）作为系统数据序列，用于说明所构造的强化缓冲序列在冲击扰动数据建模预测过程中的应用．

计算该企业月销售额的增长率分别为2．96%，4．95%，7．12%，9．94%，12．01%，11．65%，前半部分增长速度较后半部分较缓，用强化缓冲算子进行作用，以消除原始数据序列所受到冲击扰动因素的干扰．

表1 企业新产品月销售额 万元

以1—6月份数据为建模数据，以7月份数据为模拟检验数据．

用新强化缓冲算子

对原始数据进行强化，得到新的强化数据序列为

无缓冲算子进行作用时，

缓冲算子D进行作用时，

计算可得到7月份预测结果及和实际值相对误差见表2．

表2 预测数据及效果对比

由表2可以看出，用作用后的序列算子再建模，取得了良好的预测效果，显著降低了预测相对误差．因此，前文提出的强化缓冲算子有一定的实用性．在定理1中，将f（x），g（x）做一定的对称变换，可以得到相应的弱化缓冲算子．由于原理基本相同，这里不再证明．

3．2 弱化缓冲算子的应用

以上海市国际互联网用户数为例［10］，验证构造的弱化缓冲算子在GM（1，1）模型预测中的应用．选取该市2001—2007年国际互联网用户数（单位：万户）作为原始数据，有

从原始数据可以发现，上海市上网用户数增长势头很猛，年平均增长率为19．52%，如此高的增长率不可能一直保持下去，因此直接用原始数据建模，预测结果令人难以相信．笔者经过分析认为，上海市上网用户数猛增与Internet的刚刚兴起，以及政府的大力推广等因素有关，因此要进行若干年后上网用户数的预测，必须弱化其增长趋势，即将上述政策因素附加到过去的年份中，从而消除前期政策因素对后期上网用户数增加速度的影响，使得模型预测精度更高，预测结果与实际情况相符合．

以2001—2006年数据作为建模数据，以2007年数据为模拟检验数据．

用弱化缓冲算子

利用数据XD1求得对应参数：

对应的GM（1，1）模型及其时间响应式分别为：

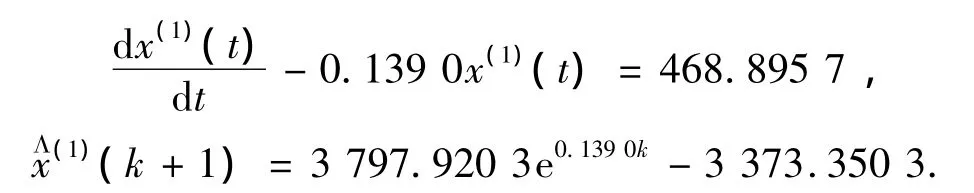
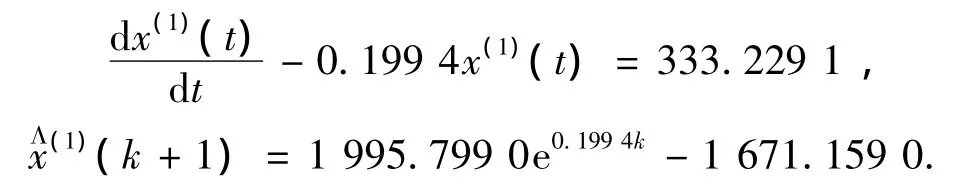
通过计算得到平均相对误差和一步预测误差的比较结果，见表3．

利用数据XD2求得对应参数：

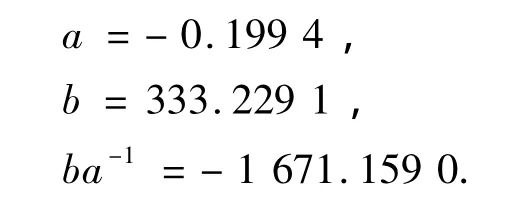
对应的GM（1，1）模型及其时间响应式分别为：

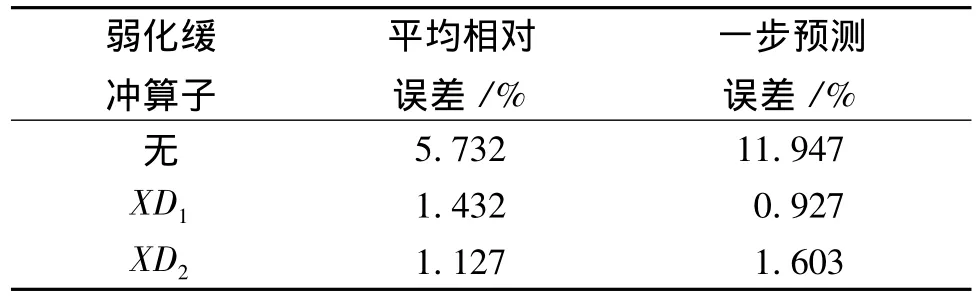
弱化缓冲算子平均相对误差/%一步预测误差947 XD1 1．432 0．927 XD2 1．127 1．603/%无5．732 11．

由表3可以看出，用缓冲作用后的数据再建模，取得了良好的预测效果，显著降低了平均相对误差．因此，这里提出的弱化缓冲算子有一定的实用性．在定理3中，将f（x），g（x）做一定的对称变换，可以得到相应的强化缓冲算子．由于原理基本相同，这里不再证明．

4 结语

在缓冲算子的构造过程中，以前都是一个一个去构造，构造相对繁琐，这里将缓冲算子的构造与函数联系起来，一次构造一大类缓冲算子，为解决扰动数据序列的建模提供了多种选择，但在运用缓冲算子对建模数据预处理的实际应用中，对于基于指数函数的缓冲算子x（k）d=f（x（k））eg（x（k））和基于余切函数的缓冲算子x（k）d=f（x（k））cot（g（x（k）））而言，函数f（x），g（x）的选取非常重要，在任何情况下选取何种函数和何种缓冲算子，使得它们相互结合后达到最佳的建模效果，此问题仍需进行深入地研究．

［1］刘思峰．冲击扰动系统预测陷阱与缓冲算子［J］．华中理工大学学报，1997，25（1）：25 －27．

［2］刘思峰，党耀国，方志耕．灰色系统理论及其应用［M］．5版．北京：科学出版社，2010．

［3］党耀国，刘思峰，刘斌．关于弱化缓冲算子的研究［J］．中国管理科学，2004，12（2）：108 －111．

［4］党耀国，刘斌，关叶青．关于强化缓冲算子的研究［J］．控制与决策，2005，20（12）：1332 －1336

［5］吴正鹏，刘思峰，米传民，等．基于不动点的新强化缓冲算子及其性质研究［J］．控制与决策，2010，25（9）：1338－1342．

［6］吴正朋，刘思峰，崔立志，等．基于单调函数的新弱化缓冲算子研究［J］．控制与决策，2009，24（7）：1055－1058．

［7］吴正朋，刘思峰，米传民，等．基于单调函数的若干实用强化缓冲算子的构造［J］．系统工程，2009，27（5）：124－126．

［8］胡小莉，吴正朋．基于单调函数的4种新强化缓冲算子及其关系研究［C］∥第19届灰色系统全国会议论文集，2010．

［9］关叶青，刘思峰．基于不动点的强化缓冲序列算子及其应用［J］．控制与决策，2007，22（10）：1189 －1192．

［10］上海统计局．上海统计年鉴［M］．上海：上海统计出版社，2008．