基于径向基神经网络滞环电流跟踪控制的有源电力滤波器

何益宏，张立涛

（五邑大学信息学院，广东 江门 529020）

随着电力电子设备及非线性负荷的大量应用，电力系统的无功需求和谐波污染日益严重．而各类电网用户对电能质量的要求却日益提高，尤其是各种数字化设备．有源电力滤波器（APF）作为柔性交流输电系统（FACTS）的核心设备之一，是近些年发展起来的一种抑制电网谐波的有效设备［1－2］．笔者在滞环跟踪控制策略的基础上建立了一个基于径向基（RBF）神经网络的滞环控制比较器取代传统的滞环控制器．该控制比较器保持了神经网络自身具有的并行处理能力和容错能力，能够实现对电流的快速跟踪和最高开关频率的限制，避免了过高的开关频率对开关器件的损害．

1 有源电力滤波器

1．1 并联式有源电力滤波器的数学模型

三线三相制并联型有源电力滤波器系统如图1所示［3］．

1．1．1 指令电流运算电路

该电路是根据补偿目的，计算出需要的补偿电流指令信号，其核心是谐波与无功电流的检测计算．

1．1．2 电流跟踪控制电路

该电路是根据指令运算电路运算得到的补偿指令，生成补偿电流，注入到电网中，从而达到有源电力滤波器抑制谐波和无功补偿的效果［4－7］．其核心由驱动电路和主电路共同组成，称作补偿电流发生电路，如图2所示．电流跟踪控制电路是APF系统中非常重要的一个部分，电流控制方法的优劣直接决定了系统补偿效果的好坏．

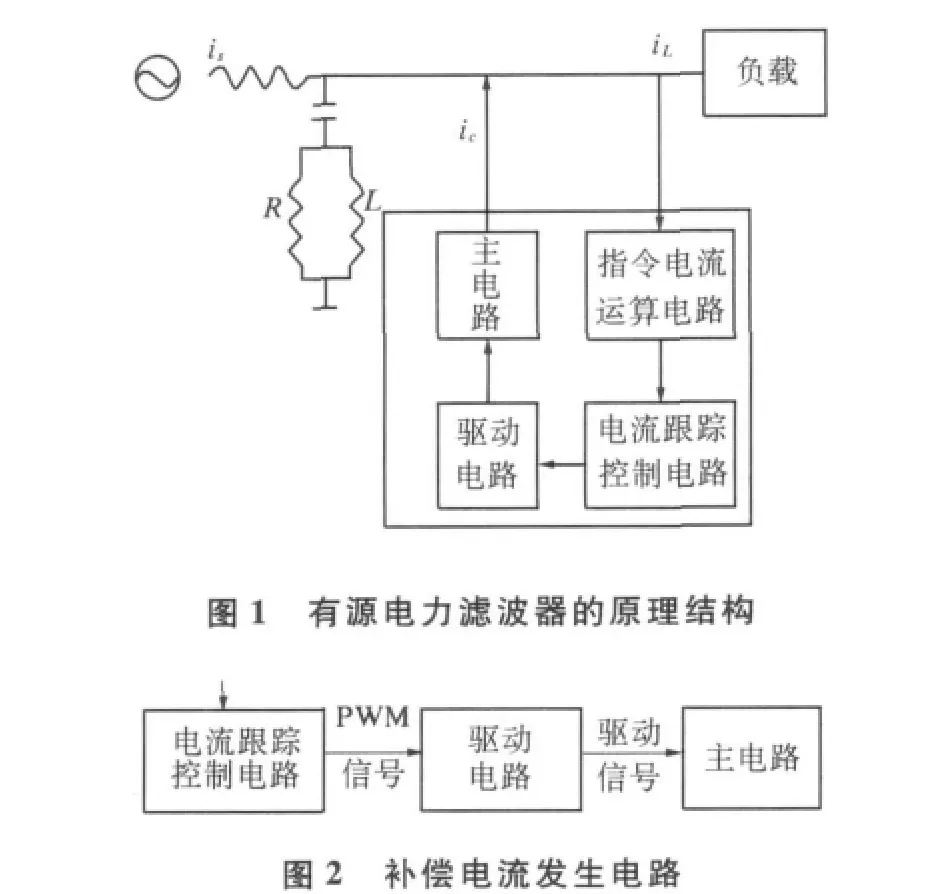
1．1．3 驱动电路

驱动电路是将电流跟踪控制电路生成的逻辑信号转换为主电路电子器件的驱动信号，控制器件的导通与断开，具有信号转换和功率放大的功能．

1．1．4 主电路

主电路的作用是根据电流跟踪控制电路和驱动电路产生的逻辑信号，生成随补偿电流指令信号变化而变化的补偿电流．

1．2 传统的滞环比较方式下的工作频率

图3是传统的滞环电流跟踪控制示意图，从图中可以看出，滞环比较器的输入是实际补偿电流信号与指令电流信号的差，这个差值经过滞环控制比较器产生控制开关信号．

图3 滞环比较电流控制原理

图4为单相有源电力滤波器拓扑结构图，在传统的滞环比较方法中，给定参考电流=Isin（nωt），并且认定在一个电流周期内不变．APF工作时直流侧电压为UDC，网侧电压为Us．

图4 单相APF结构图

假定忽略逆变器上桥臂开关器件通断时的死区时间，当开关管S1，S4导通时，则

由滞环比较器动作条件，可得到开通时间

当开关管S2，S3导通，S1，S4关断时，逆变器内部桥臂换流，有

由滞环比较器动作条件，可得到关断时间为

则器件的开关周期为两者的和，为

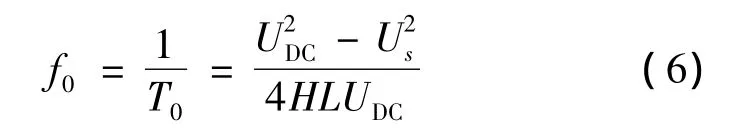
因为在整个周期内，网测电压Us是一个时变的正弦量;而直流电压UDC基本保持不变，可以看作是一个恒定的量．所以，整个周期内的开关频率是不断变化的，将f0对时间求导可得

则器件的开关频率为

由式（7）可以得出，当电网电压经过零点时，器件的开关频率最高;如果滞环宽度不变，开关器件的开关频率受电流变化幅度的影响比较大;当电流变化幅度很大时，并且电流幅值较小时，因为环宽固定，这样可能造成补偿电流的性能较差，误差也可能变大;当电流值很大时，环宽固定，会使开关器件的开关频率随之增大，可能损坏开关器件［4］．所以传统的滞环比较器虽然具有响应快且精度高的优点，但是开关频率波动很大，在器件最大开关频率的容许范围内，无法得到较高的跟踪精度［3］．

为避免此种情况，近年来很多文献提到了定时滞环比较电流的跟踪控制方法，如图5所示．这种方法是在传统滞环比较的方法上增加一个定时比较器，比较时间固定，所以可以避免因为开关器件开关频率太高而损坏的现象，同时开关器件的频率固定不变．但这种方法会造成很大的跟踪电流误差［1］．

笔者在滞环控制策略的基础上训练一个RBF神经网络滞环控制比较器最终取代传统的滞环控制器，以避免过高的开关频率对开关器件的损害．

图5 定时滞环比较电流控制原理

2 径向基神经网络

2．1 人工神经网络

人工神经网络（Artificial Neural Network，ANN）本身具有强大的学习能力，可以实现非线性映射过程，并且具有大规模计算的能力，而在计算机、自动化及人工智能方面都得到广泛的应用［8－13］．

人工神经网络的特点如下：①对输入、输出信号不需要明确的函数关系;②高度的全局非线性作用，能够使其充分逼近复杂的非线性关系，实现任意的非线性映射;③具有高度的并行性，使其具有较高的运算能力和比较快的运算速度;④自适应的学习能力，使其具有能够学习没有见过的模式等［8］．

由于电力滤波器（APF）本身就是一个具有强耦合性的非线性系统，用传统的自动控制理论对电力滤波器（APF）进行解析模型上存在的误差．将人工神经网络应用于APF控制策略可实现：①计算量小且检测精度高;②数据敏感度低，对参数的依赖性小;③实时性良好;④抗干扰能力好，能克服噪声等的影响．这些优点可解决APF的技术瓶颈．文中主要研究如何将神经网络算法移植到APF系统中的谐波指令电流跟踪环节上．

2．2 径向基神经网络

径向基函数（RBF）神经网络（如图6所示）是一个只含一个隐含层的3层前馈型神经网络．隐含层的转换函数是局部响应的高斯函数．由于局部响应的特点，其网络的神经元数目比较多，所需要的训练时间少很多，且可以任意精度地逼近连续函数［9］．

图6 单径向基神经网络模型

输出层的输入为隐含层神经元输出的加权求和．由于激励函数为纯线性函数，所以输出为

RBF的训练过程分2步：第1步为无教师学习，确定训练输入层与隐含层的权值w1;第2步有教师学习，确定训练隐含层与输出层权值w2．在训练前要提供输入矢量X和对应的目标矢量T．训练的目的是求取2层的最终权值w1，w2和阈值b1，b2．

3 径向基神经网络的滞环跟踪控制

传统滞环控制器是将误差信号直接送入滞环比较器得出PWM驱动信号，而径向基神经网络滞环控制的滞环比较功能是通过训练才能获得．径向基神经网络滞环控制器的基本思路是训练一个神经网络实现滞环控制的基本功能，并同时保持神经网络自身的并行处理能力、容错能力，能够实现对电流的快速跟踪．径向基神经网络滞环控制器的样本是通过对带有实际滞环控制比较器的电路采样获得，对于规律变化的负载，一个周期的训练样本即可［14－17］，神经网络的输出逼近期望的滞环控制器的PWM控制波形．

训练样本的获得是通过对普通滞环比较器有源滤波器的输入、输出进行采样得到的．选择500组采样数据对径向基神经网络进行训练，训练后选择10组数据进行处理验证，将神经网络输出的数据与理想PWM信号数据进行比照，符合PWM信号产生模块的驱动要求．数据对比见表1．

表1 3种数据结果的对比

训练好的径向基神经网络编写入MATLAB中的S－函数并封装成S－函数模块，用能够实现滞环控制功能的S－函数模块代替仿真模型中的滞环比较器，通过实时采样Δic信号并运算处理输出控制电流逆变电路的PWM信号，从而实现电流的跟踪．

4 仿真结果

使用MATLAB/Simulink软件搭建了有源滤波器的仿真模型，选用三相三线制输电线路，以三相晶闸管全桥整流电路作为非线性负荷谐波源负载，APF系统的仿真参数为：①电网线电压有效值Us=380 V;②进线电感值L=1 mH;③直流侧电容值C=4 500 μF．

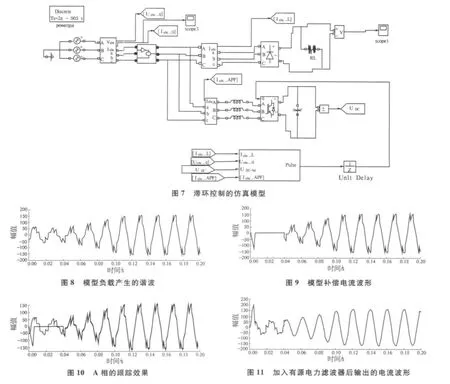
在此基础上对提出的基于径向基神经网络滞环控制算法进行验证．仿真模型如图7所示，模型负载产生的谐波如图8所示，模型补偿电流波形如图9所示．

在模型仿真0．04 s时加入电流跟踪模块后产生的电流补偿波形如图9所示．Δic电流（A相）的跟踪效果如图10所示．在0．04 s时APF开始加入系统进行工作，0．01 s后Δic的跟踪正常，满足设计要求．加入有源电力滤波器后电源的输出电流波形如图11所示．从图11可以看出，在0．1 s时系统电源输出波形趋于稳定，且呈正常正弦波形．

5 结语

提出的滤波器跟踪控制算法相对于传统的滞环控制电流跟踪算法，降低了开关器件因开关频率过高引起损坏的几率．实验结果进一步验证了该算法的电流跟踪效果以及对非线性装置产生的系统谐波的补偿能力．该算法不仅能够满足动态性能和控制精度的要求，同时具有较强的鲁棒性和自适应性．

［1］何益宏，梁春贤，欧阳．基于DSP的有源电力滤波器控制系统研制［J］．广西电力，2002（3）：64－66．

［2］卓放，何益宏，李红雨，等．大容量有源电力滤波器实现方法的研究［J］．电力电子技术，2001（2）：13－15．

［3］刘毅，徐世．基于改进的滞环控制策略的并联型有源电力滤波器仿真研究［J］．工矿自动化，2010（6）：34－37．

［4］林海雪，孙树勤．电力网中的谐波［M］．北京：中国电力出版社，1998：43－55．

［5］姜齐荣，赵东元，陈建业．有源电力滤波器·结构·原理·控制［M］．北京：科学出版社，2005：20－68．

［6］ Elmitwally A，Abdelkader S，Elkateb M．Universal power quality manager with new control scheme［J］．IEEE Proceedings—Generation Transmission and Distribution，2000，147（3）：183 －189．

［7］ Vinod Khadkikar，Ambrish Chandra．A novel structure for three-phase four-wire distribution system utilizing unified power quality conditioner（UPQC）［J］．IEEE Transactions on Industry Applications，2009（45）：1897 －1902．

［8］罗四维．大规模人工神经网络理论基础［M］．北京：清华大学出版社，2004：35－46．

［9］田雨波．混合神经网络技术［M］．北京：科学出版社，2009：59－73．

［10］噶哲学，孙志强．神经网络理论与MATLAB2007实现［M］．北京：电子工业出版社，2007：117－131．

［11］周开利，康耀红．神经网络模型及其MATLAB仿真程序设计［M］．北京：清华大学出版社，2005：101－110．

［12］刘新平，唐磊，金有海．一种简单的BP网络隐层扩展模型及其训练算法研究［J］．化工自动化及仪表，2008，35（2）：21 －24．

［13］史峰，王小川，郁磊，等．MATLAB神经网络30个案例分析［M］．北京：北京航空航天大学出版社，2010：11－19．

［14］罗安．电网谐波治理和无功补偿技术及装备［M］．北京：中国电力出版社，2006：15－47．

［15］徐德鸿．电力电子系统建模及控制［M］．北京：科学出版社，2006：9－31．

［16］尹慧，许彦．有源电力滤波器的研究现状及前景展望［J］．电力电容器与无功补偿，2010（3）：27 －32．

［17］刘心肠，王杰，王昕，等．源滤波器的模糊阈值变环宽滞环电流跟踪控制策略［J］．电力系统保护与控制，2011，39（11）：116 －122．