形态学分水岭算法在粘连图像分割中的应用

张 芹，侯德文

（山东师范大学 信息科学与工程学院，山东 济南 250014）

图像分割是将图像中有意义的特征或者需要应用的特征提取出来，这些特征可以是图像的原始特征（如物体占有区的像素灰度值、物体轮廓曲线和纹理特征等），也可以是空间频谱或直方图特征等。图像分割是图像处理进入到图像分析的关键步骤，也是图像理解的基础，一方面，它是目标表达的基础，对特征测量有重要的影响；另一方面，由于图像分割及其基于分割的目标表达、特征提取和参数测量等将原始图像转化为更抽象、更紧凑的形式，使更高层的图像分析和理解成为可能。

常用的图像分割算法有阈值分割算法[1]、区域分割算法[2]、边缘检测算法[3-4]以及分水岭算法等[5-6]。 其中，分水岭算法因具有计算速度快、边界定位准确等优点而被广泛应用到粮食颗粒分割领域，但它本身存在严重的过分割问题，因此，有效降低过分割问题是目前人们研究的焦点之一。

目前主要有两类方法解决分水岭算法的过分割问题：一类是对原图像进行预处理，它是基于标记提取的分水岭分割算法[7]，每一个标记对应着图像中的一个物体；另一类是对图像分割后再进行处理[8]，根据某种准则进行区域合并。本文重点研究第一类解决方法。

1 数学形态学理论

1.1 形态学基本理论

数学上，膨胀定义为集合运算。A被B膨胀，记为A⊕B，定义为：

腐蚀的数学定义与膨胀相似，A被B腐蚀记为AΘB，定义为：

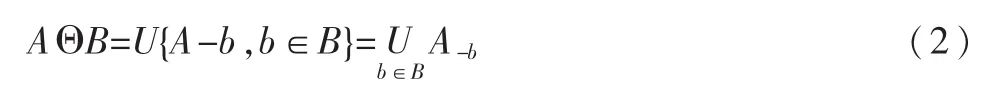
集合B对集合A作开运算是指集合A被集合B腐蚀后再用B来膨胀腐蚀结果，表示为AoB，其定义为：

集合B对集合A作闭运算是指集合A被集合B膨胀后再用B来腐蚀膨胀结果，表示为 A·B，其定义为：

1.2 形态学梯度

形态学梯度的计算是为了突出图像中灰度级变换较大的部分，因此，可以利用原始图像与图像腐蚀或膨胀处理之后的图像进行差分来计算形态学梯度。对于图像A以及结构元素B，常用的形态学梯度有以下几种定义方法[9]：

定义1 膨胀图像与腐蚀图像之间的算术差：

定义2 原始图像与腐蚀图像的算术差：

定义3 膨胀图像与原始图像之间的算术差：

图1给出了在圆形结构元素作用下得到的不同的形态学梯度。用尺寸为1的圆形结构元素作膨胀，得到的图像边界向外扩张了一个单位像素宽度，作腐蚀得到的图像边界向内收缩一个单位像素宽度，因此用定义1得到的梯度图像边界扩大了两个单位像素宽度，而用定义2和定义3得到的梯度图像的边界宽度不变。

2 分水岭变换算法及其改进

2.1 算法原理

分水岭分割算法的思想源于测地学中的地膜形态模型。VINCENT L[10]于1991年提出了著名的基于浸沉的分水岭算法。其原理描述如下：首先将一幅图像视为跌宕起伏的地貌模型，图像中每个像素的灰度值对应地形中的高度（即海拔），将均匀灰度值的局部极小区域视为盆地，并在最低处穿孔，使水慢慢地均匀浸入各个孔，当水将填满盆地时，在某两个或多个盆地之间修建大坝。随着水位的不断上升，各个盆地完全被水淹没，只剩没被淹没的各个大坝，并且各个盆地也完全被大坝所包围，从而可以得到各个大坝（即分水岭）和各个被大坝分开的盆地（即目标物），最终达到分割粘连物体的目的。

2.2 顶帽变换

顶帽（top-hat）变换即从原图像中减去开运算的图像，这样，原图像中与结构元素相匹配的区域就得到增强，从而达到从图像中提取给定目标体的目的。

本文对顶帽变换后的图像进行处理，首先用尺度为1～n的结构元素对图像进行腐蚀，当腐蚀到所有的目标都分离时停止腐蚀。然后用尺度为2～n的结构元素进行膨胀。图 2（a）为顶帽变换的图像，图 2（b）为对顶帽变换进行改进的图像。从图2可以看出，经过对顶帽变换图像的处理，物体之间的粘连明显减少。

2.3 形态学多尺度梯度

考虑式（6）的形态学梯度，结构元素的尺寸和形状会对梯度图像产生一定影响[11]。

不同尺度结构元素的形态学梯度如图3所示。图3（a）为原始图像，图 3（b）～图 3（h）为用尺度为 1～7 的圆形结构元素得到的梯度图像，图 3（i）～图 3（l）与图 3（m）～图 3（p）分别是用尺度为 1～4的菱形和方形结构元素得到的梯度图像。从图3可以看出，随着结构元素尺度的增大，得到的梯度图像的边界厚度也在增大；此外，不同结构元素产生的梯度图像也有所不同。这充分说明在形态学运算中结构元素选择的重要性。结构元素形状的选择由原始图像中包含的形状特征而定，如对于大米图像，结合其椭圆形的形状特性，一般用圆形结构元素来处理。

为了减少结构元素的尺寸对梯度图像边界的影响，通常采用多尺度形态学梯度[9]：

本文采用改进的多尺度形态梯度，其定义为：

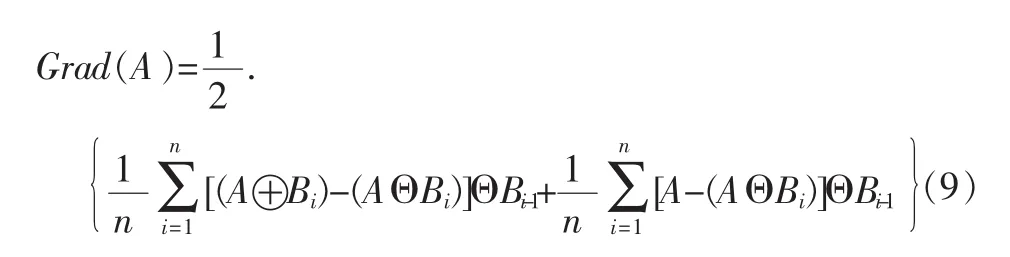
式（8）为对于尺度为i的梯度图像利用尺度为 i-1相同结构元素对其进行腐蚀来减小边界，但边界减少的同时也使边界变得模糊，因此本文采用式（9），以使边界既清楚又不至于太粗。图4给出了由式（5）得到的梯度图像图、由式 （8）得到的多尺度梯度图像图和由式（9）得到的改进的多尺度梯度图像。

从图4可以看出，改进的多尺度梯度图像解决了由结构元素的尺寸增大而引起的梯度图像边界增大的问题，而且边界更加清晰。

3 实验结果

3.1 分割算法实现

分割算法实现的步骤如下：

（1）将大米图像进行顶帽变换，并对顶帽变换的图像进行处理；

（2）应用Ostu方法局部阈值处理步骤（1）得到的图像；

（3）运用多尺度梯度获得梯度图像；

（4）运用分水岭算法分割图像。

图5给出了使用不同阈值处理方法得到的图像。其中，图5（a）为应用 Ostu方法进行的局部阈值处理的图像，图5（b）为应用全局阈值处理的图像。

由图5可以看出，局部阈值处理能够很好地解决光照不均、背景灰度变化以及全局阈值不宜分割图像等问题。

3.2 实验结果

为了验证本算法的有效性，分别采用本算法和标记分水岭算法在Matlab7.0中对米粒图和按钉图进行了分割，结果如图6和图7所示。本算法与标记分水岭算法在分割区域个数与执行时间上的对比如表1所示。

表1 标记分水岭算法与本文算法的对比

由图6和表1可以看出，虽然本算法比控制标记符的分水岭算法执行的时间长，但分割效果更好，几乎不存在过分割和欠分割现象。

本文通过运用顶帽变换和改进的多尺度形态学梯度来改进形态学分水岭算法，有效地改善了光照不均、噪声和结构元素的形状和尺寸对图像分割的影响，在一定程度上改善了分水岭算法的过分割问题。实验证明，该算法有效减少了分割区域的个数。单就形态学分水岭算法而言，虽然计算复杂性增加了，但对于粘连分割的效果理想，为后续的工作奠定了良好的基础。

[1]崔明，孙守迁，潘云鹤.基于改进快速分水岭变换的图像区域融合[J].计算机辅助设计与图形学学报，2005，17（3）：546-552.

[2]高丽，杨树元，李海强.一种基于标记的分水岭图像分割 新 算 法[J].中 国 图 象 图 形 学 报 ，2007，12（6）：1025-1032.

[3]张立东，毕笃彦.一种基于洪水消退模型的快速分水岭算法[J].模式识别与人工智能，2006，19（3）：349-360.

[4]许向阳，宋恩民，金良海，等.边缘和区域多阶段结合的图像分割[J].小型微型计算机系统，2011，32（5）：943-946.

[5]张鲲，王士同.一种顺序无关的改进分水岭图像分割算法[J].计算机应用，2008，28（4）：969-972.

[6]蔡念，唐孝艳，许少睿，等.基于分水岭算法的 MELK图像分割[J].计算机应用研究，2009，26（8）：3175-3176.

[7]Gao Hai， Siu Wanchi， Hou Chaohuan.Improved techniques for automatic image segmentation[J].IEEE Transactions on Circuits and Systems forVideo Technology， 2001，11（12）：1273-1280.

[8]O′CALLAGHAN R J， BULL D R.Combined morphologicalspectral unsupervised image segmentation[J].IEEETransactions on Image Processing， 2005，14（1）：49-62.

[9]谢文娟.基于改进分水岭算法的细胞图像分割[D].武汉：中南民族大学，2010.

[10]VINCENT L， SOILLE P.Watersheds in digital spaces：an efficient algorithm based on immersion simulations[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1991，13（6）：583-598.

[11]商艳丽，夏志成.基于形态学多尺度算法的肺部CT图像边缘检测[J].自动化与仪器仪表，2008（1）：43-45.

[12]GONZALEZ R C， WOODS R E， EDDINS S L.数字图像处理（MATLAB版）[M].阮秋琦，译.北京：电子工业出版社，2009.