稳定的特征选择研究*

李云

（南京邮电大学 计算机学院，江苏 南京 210003）

随着信息技术和生物技术的快速发展，在现实生活及科学研究中产生大量的高维海量数据。为了从大规模数据中挖掘出有用的知识，特征选择已成为高维数据分类或者回归中的关键问题[1]，目前已被广泛应用于文本分类、图像检索、基因分析和入侵检测等。所谓特征选择就是从一组特征中挑选出一些最有效的特征以达到降低特征空间维数或者发现自然模型真实变量的过程，其通常包括两个关键问题：搜索策略和评价准则。参考文献[2-4]对已有特征选择方法以及特征选择统一框架进行了全面的综述。特征选择算法根据训练的数据集中样本有无标记通常分为监督、非监督和半监督特征选择算法。在评价过程中，监督的特征选择方法通常通过评价特征与类别之间的关联性或者特征的分类性能来获取特征的相关性。非监督的特征选择方法通常通过探究未标记数据分布特性来获取特征的相关性。半监督特征选择方法则同时利用标记的和未标记的样本。此外，根据评价准则，特征选择又可以分为过滤器、封装器以及嵌入式三类基本模型[2]。过滤器模型是将特征选择作为一个预处理过程，利用数据的内在特性对选取的特征子集进行评价，独立于学习算法。封装器模型则将后续学习算法的结果作为特征子集评价准则的一部分。嵌入式模型则试图利用前两种模型的优点，在不同的搜索阶段利用不同的评价准则。一般而言，过滤器的时间复杂度比封装器低，且结构相对简单，因此广泛用于对高维数据的处理。如果根据输出结果来区分，特征选择又可以分为两种[3]：一种是输出所有特征权重，并对其进行排序，如 Lmba[5]、SQP-FW[6]等；另一种是输出选择的特征子集，如 SVM-RFE[7]等。

1 稳定性分析

特征选择的一个重要特性是发现自然模型的真实变量，在很多应用场景下，特征选择所选取的特征或者变量应该是具有可解释性的。如在文本分类中，本研究利用一些先验知识很容易检查所选择的单词对分类是否有意义。此外在基因数据处理中，所选择的基因也可以解释。但是，如果当收集的某种病例样本发生变化时，特征选择算法获取的基因子集或者排序结果差别较大，那么专家就会对基因选择结果产生疑虑，而且也给结果的验证带来不便，从而难以确切获得解释该疾病的相关基因组。因此在某些领域，特征选择的稳定性也是至关重要的。特征选择的稳定性是对所选择的特征子集相似性度量。它主要研究当样本或者算法自身的参数有变化时，特征选择算法的鲁棒性。也就是说，对于高维数据的分类或者回归，其主要任务有两个：一个是设计尽可能好的算法，以获取对未知样本较高的预测能力；另一个是除了进一步提高算法的性能，还要能深入理解特征与样本输出之间的关系[1]。对于这第二个任务来说，除了要提高特征选择的分类性能外，还需要关注其稳定性，否则第二个任务将难以完成。不稳定的特征选择结果将带来很多歧义，难以获取可以理解的真实特征（变量）。

1.1 稳定性因素

产生不稳定特征选择结果的主要因素有：

（1）数据扰动。数据扰动包括两个方面：①数据本身变化，包括数量变化和训练样本分布的不同；②添加噪声特征。

（2）算法本身没有稳定机制。已有的算法在设计特征选择评价准则时，只是考虑了分类性能或者聚类性能，而没有关注算法的稳定性。

（3）当特征集里含有大量的冗余特征时，由于冗余特征之间的关联性较强，具有相似的（分类）性能，也会产生多个具有近似性能的特征子集，从而影响算法的稳定性。

（4）高维小样本。由于这类数据的训练样本较少，而特征维数非常高，如基因数据等，虽然训练样本只有细微的变化，而特征选择的结果将发生很大变化。

为了有效提高特征选择算法的稳定性，目前主要有基于经典特征选择算法的集成特征选择[8]、基于样本加权的算法[9]和特征组群的方法[10]。

1.2 稳定性度量

特征选择的稳定性是对所选择的特征子集相似性度量。它主要研究当样本或者算法自身的参数有变化时，特征选择算法的鲁棒性。所有特征选择结果的相似性越大，则认为特征选择的稳定性越高。而整体的稳定性就是所有特征选择结果的相似之和的平均值：

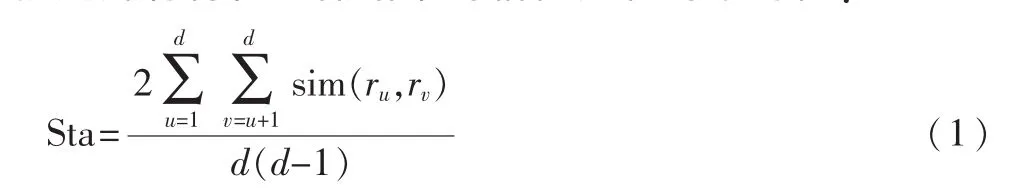
式中，如果以特征排序为例，其中ru、rv表示第u和第v个特征排序结果，其长度为特征的维数n；sim表示排序结果之间的相似性；d为特征排序结果的个数。采用Spearman排序关联系数来计算特征排序结果之间的相似性：

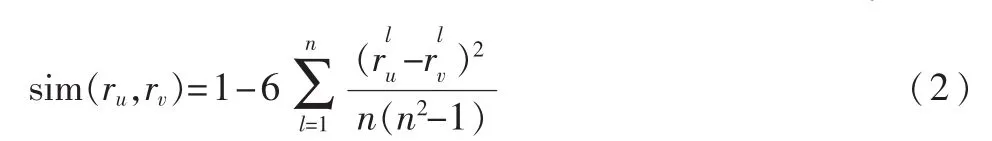
式中，rlu表示第l个特征在ru中的排序值，一般假定按降序排序，则排在最顶端的特征其排序值为n，而后依次减1。

2 集成特征选择

与集成学习相类似，集成特征选择包括两个必不可少的步骤：一是产生多个不同的基特征选择器，二是将每个基特征选择器的结果进行集成。而生成不同的特征选择结果可以采用不同的方法，如采用不同的特征选择方法、基于不同的训练子集等。而结果的集成可以采用加权投票等，假设对于包含有m个特征排序结果的集合，则利用加权投票得到的集成特征选择结果可以表示为：

3 样本加权

已有理论分析结果表明，特征选择的稳定性与特征选择结果的偏差相关，而有效减少方差的方法是：可以根据样本对特征相关性的影响赋予不同的权重，然后基于带权的训练样本进行特征选择。也就是对重要区域内的样本赋予较高的权重，而不重要区域内的样本赋予较小的权重。其中方法之一是根据样本中不同特征相关性的局部轮廓（Local Profile）来获取样本的权重。而对于某个样本 x，其第 j个特征的局部轮廓 x′j的定义如下：

式中，xM表示与x不同类的最近邻样本，而xH表示与x同类的最近邻样本。特征的局部轮廓是样本的假设间隔在各个特征维上的分解。

将原始空间上的样本映射到由各个特征的局部轮廓所构建的间隔矢量特征空间，则对特征相关性有着不同影响的样本偏离对特征相关性具有类似影响的样本比较远；具有类似影响的样本通常比较多，占大多数，而其他样本比较少。为了提高特征选择的稳定性，需要对那些偏离大多数的样本赋予较小的权重，减少它们的影响。其权重计算公式如下：

式中，x′为样本x在间隔矢量空间上的映射样本。

本文对特征选择研究的热点——稳定的特征选择（包括稳定性的定义、因素和度量等）进行了详细的分析，并详细介绍了集成特征选择和样本加权两种提高特征选择稳定性的方法，以供参考。

[1]FAN J Q，LV J C.A selective overview of variable selection in high dimensional feature space[J].Statistical Sinica，2010（10）：101-148.

[2] LIU H， YU L. Toward integrating feature selection algorithms for classification and clustering[J].IEEE Transaction on Knowledge and Data Engineering， 2005， 17（3）：1-12.

[3]ZHAO Z.Spectralfeature selection forminingultrahigh dimensional data[M].Arizona State University PhD Dissertation，2010.

[4]GUYON I，ELISSEEFF A.An introduction to variable and feature selection[J].Journal of Machine Learning Research，2003，3（3）：1157-1182.

[5]LI Y，LU B L.Feature selection based on loss margin of nearest neighbor classification [J]. Pattern Recognition，2009，42：1914-1921.

[6]TAKEUCHI I，SUGIYAMA M.Target neighbor consistent feature weighting for nearest neighbor classification[C].Conference on Advances in Neural Information Processing Systems（NIPS）， 2011：1-9.

[7]GUYON I， WESTON J， BARNHILT S， et al.Gene selection for cancerclassification using supportvectormachine s[J].Machine Learning， 2002，46：389-422.

[8]SAEYS Y， ABEL T， PEER Y V.Robust feature selection using ensemble feature selection techniques[C].Proceeding of the European Conference. on Machine Learning and Principles and Practice of Knowledge Discovery in Databases（ECML-PKDD）， Lecture Notes on Artificial Intelligence，2008，5212：313-325.

[9]YU L， HAN Y， BERENS M E.Stable gene selection from microarray data via sample weighting[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics， 2012，9 （1）：262-272.

[10]LOSCALZO S， YU L， DING C.Consensus group stable feature selection[C].Proceeding ACM SIGKDD Conference.on Knowledge Discovery and Data Mining （KDD）， Paris France， June 28-July 1.2009：567-575.