基于有限元仿真技术的曲轴疲劳强度分析

骆清国， 杨良平， 王旭东， 马 强

(装甲兵工程学院，北京 100072)

当前，高功率密度柴油机已经成为重要的发展趋势.德国MTU公司开发的小缸径高功率密度(HPD)MT890系列柴油机的单位体积功率达到1200－1300 kW/m3.其中，12V890柴油机较其相同功率的MT883Ka-501柴油机，整机质量和体积均减少约50%［1］.提高功率密度意味着减小曲轴尺寸，因此，曲轴的疲劳强度分析变得尤为重要，与基于试验的传统方法相比，有限元疲劳仿真能够在设计阶段判断零部件的疲劳寿命薄弱位置，避免不合理的寿命分布，同时能缩短产品的开发周期，降低设计成本［2］.文中采用有限元仿真技术对某中大型柴油机曲轴进行自由模态分析和疲劳寿命计算，为曲轴的优化设计提供理论依据.

鉴于试验验证需要大量的人力物力和漫长的实验周期，对曲轴材料S-N曲线的相关试验数据进行拟合修正，建立曲轴的疲劳累积损伤半经验公式，对仿真得到的曲轴寿命进行了验证.

1 动力学仿真

1.1 曲轴有限元模型的建立

建立某中大型柴油机的曲轴模型，并进行有限元网格划分，得到65 493个节点，41 265个单元.设置曲轴材料为42CrMo，弹性模量为2.1e11Pa，泊松比为0.3，密度为7 850 kg/m3.在曲轴的连杆轴颈、主轴颈和飞轮连结处建立外接节点单元，即MPC-RBE2单元，为了实现MPC-RBE2单元在刚-柔性体间的载荷传递功能，其位置与曲轴在Adams中各运动副的Marker点位置必须完全一致.曲轴有限元模型及MPC-RBE2单元位置见图1.

图1 曲轴的有限元模型

1.2 刚柔耦合模型的建立

图2 曲柄连杆机构刚柔耦合模型

1.3 约束和外载荷

根据曲柄连杆机构的实际运动关系建立运动副．根据发动机台架实验测得的数据建立气缸压力样条曲线，将其施加在活塞顶上.在多体动力学模型中，6个气缸按照一定的相位关系，以曲轴转角为自变量分别调用各缸气体作用力数据文件.图3是转速为1 500 r/min时，一个工作循环内各缸气体作

将模态分析后得到的曲轴模态中性文件通过Adams/FLEX模块导入Adams替换原刚性曲轴，得到刚柔耦合动力学模型.采用多柔体动力学仿真分析计算曲轴应力、应变，一方面可以考察曲轴的强度、应力集中等是否满足要求，同时也为准确分析曲轴的疲劳寿命提供条件，曲柄连杆机构刚柔耦合模型见图2.用力曲线.各缸出现峰值的间隔为120度曲轴转角.

测量曲轴转角α和连杆摆角β，并依此为自变量，求得发动机的输出转矩

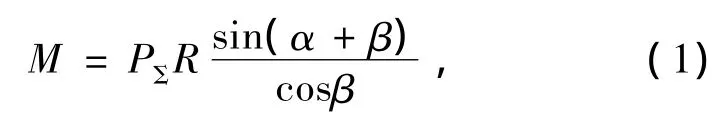
式中：PΣ为作用在活塞销中心处的合力;R为曲柄臂长度.将此转矩作为阻力矩加在曲轴输出端，使发动机运转保持平稳.

1.4 刚-柔性体动力学仿真分析

将曲轴进行柔性化处理以后，在活塞顶部加载4个工作循环的气体压力，并在Adams中进行动力仿真，仿真持续时间t=8×60/1500=0.32 s，设置步长为320.仿真过程中，曲轴整体受力及应力云图如图4所示.

图4 曲轴动态加载及应力云图

可以看出，曲柄销与曲柄臂的过渡圆角处为应力集中最严重的部位，其应力值在90.58 MPa至432.92 MPa之间.

2 曲轴的模态分析和模型降阶

2.1 曲轴模态分析

曲轴的柔性体含有11个连接点 (MPC-RBE2单元)，即模型的约束模态为66个.根据经验设定模型标准模态为26个，因此，必须在Adams中定义92个模态.计算过程如下．

约束模态：6DOF×11连接点=66模态

26个标准模态+66个约束模态=92个总模态

标准正交化后相当于：

6个刚体模态+86个弹性体模态=92个总模态［3］．

在有限元软件Patran中，采用Lanczos法计算曲轴的模态，得出曲轴各阶自由模态的固有频率和振型，舍去前6阶的刚体模态，以曲轴不为零的固有频率作为第1阶模态频率.前6阶模态频率和振型如表1所示.

表1 曲轴前6阶模态频率和振型

通过对曲轴的各阶模态振型进行分析得到曲轴在低阶频率下，主要是以弯曲模态为主，并且弯曲变形的最大部位出现在曲柄臂和曲柄销结合处，如图5所示;随着模态频率的提高，扭转模态振型趋于明显，如图6所示;随着模态频率进一步提高，出现各部分不同步的弯曲、扭转或弯扭组合振动以及复杂的局部振动，如图7所示;当模态频率超出一定范围，它们所对应的临界转速远远超出曲轴的转速范围，发生扭转共振的概率几乎为零，研究中不予考虑，如图8所示.曲轴的裂纹大多是由弯曲力矩疲劳破坏产生的，因此，研究曲轴的低阶模态在外加载荷作用下的动态应变，对曲轴的疲劳强度分析具有十分重要的作用.

图5 第1阶模态振型

2.2 曲轴模型降阶

为解决动态仿真分析和寿命计算中自由度数目多、求解困难的问题，进行模型降阶意义重大．经过有限元模态分析和动力学仿真验证，得知有些模态 (大多是较高阶的模态)对系统动力响应影响很小，首先将频率在3 000 Hz以上的模态舍去，然后根据各阶模态对应变能的贡献大小进行模型降阶，最终模型的模态数由原来的86阶降至25阶．

3 曲轴的疲劳寿命计算与验证

3.1 曲轴的疲劳寿命计算

柴油机在工作过程中，曲轴承受的实际载荷非常复杂，所受到的平均应力不会刚好为零，因此，在用Fatigue进行疲劳计算时采用Goodman法对平均应力进行修正.在输入曲轴的材料特性后，Fatigue将曲轴在外载荷作用下所受到的应力值与曲轴材料的疲劳极限结合起来，计算出曲轴的疲劳寿命.疲劳寿命云图如图9所示.

图9 曲轴疲劳寿命云图

从图中可以看出曲轴最先产生疲劳破坏的部位和图4显示的应力集中部位一致，位于曲柄销和曲柄臂的过渡圆角处，节点27 542在最大工况 (1500 r/s)下经过4.57×106次循环加载，即柴油机运行1.828×107个工作循环曲轴产生疲劳破坏.

3.2 曲轴的疲劳寿命计算验证

以应力值50 MPa为起点，每50 MPa作为一个应力分段，对曲轴最大应力节点27 542四个工作循环仿真得到的应力时间历程用雨流计数法进行计数，得到的结果如表2所示.

表2 节点1754应力历程雨流计数法统计结果

根据雨流计数结果，将连杆的载荷幅值分为4级，各级幅值与最大值之比依次为：0.85，0.725，0.275，0.125［4］.由此可得到各级应力幅值由高至低依次为：367.98 MPa，313.82 MPa，119.05 MPa，54.12 MPa.

针对曲轴的材料特性 (42CrMo钢)，对Basiquin 方程［5］进行拟合得到式中：σa和Nf分别是作用应力幅和对应的疲劳断裂周次 (材料的S-N决定);σ'f和b分别是材料疲劳强度系数和疲劳强度指数.通过对42CrMo的S-N曲线的相关试验数据［6］进行拟合修正，求得σ'f=489.75，b=0.29，由式 (2)变形有

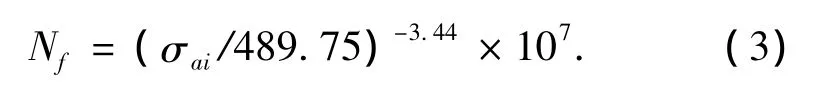
将曲轴有限元模型中最大应力节点的应力时间历程经雨流计数法计数得到的各分级应力代入拟合公式 (3)中，计算得到各分级应力对应的疲劳周次，如表3所示.

表3 各级应力对应疲劳周次

采用线性Miner法则，分别对仿真过程各级应力损伤和进行统计，可以得到其损伤和

由于柴油机在运行过程中，其载荷谱随着各缸的做功状况发生着改变，载荷谱的高、低载荷的排列形式和作用次序决定了Miner法则中D的分散性，大量试验研究结果表明，D值的范围为0.3－3.0之间.因此，D=1.114在合理范围之内，可以判定基于有限元仿真技术的疲劳强度分析结果是合理的.

5 结论

1)对曲轴进行了模态分析，从模态振型图可以看出，曲轴的结构振动模态在低频段为简单弯曲、扭转振动模态;在高频段为各部分不同步的弯曲、扭转或弯扭组合振动以及复杂的局部振动模态.

2)建立了曲柄连杆机构的刚柔耦合模型，进行了刚-柔性体系统动力学仿真分析，得到了曲轴工作过程中的应力分布云图，用Fatigue软件得到了曲轴的疲劳寿命云图，发现连杆疲劳破坏最先产生于曲柄臂和曲柄销的过渡圆角处.

3)对通过Fatigue软件得到的曲轴疲劳寿命进行理论验证.采用雨流计数法和线性Miner法则验证了基于有限元仿真技术的曲轴疲劳强度分析结果是合理的.

［1］ 张玉申．高功率密度柴油机及其关键技术 ［J］．车用发动机，2004(3)：5-8．

［2］ 周传月，郑红霞，罗慧强，等．MSC．Fatigue疲劳分析应用与实例 ［M］．科学出版社，2005．

［3］ 李 军，刑俊文．ADAMS实例教程 ［M］．北京理工大学出版社，2002．

［4］ 赵少汴，王忠保．抗疲劳设计—方法与数据 ［M］．机械工业出版社，1997．

［5］ Jorge Rodraiguez Duraan，Jaime Tupiassau Pinho de Castro．Prediction of Fatigue Crack Propagation Under Complex Loading Using Gen Parameters［C］．SAE Technical Paper，2001：4063-4067．

［6］ 王威强，徐楠山，贺庆强．42CrMo硬齿面齿轮虚拟全寿命的试验与分析 ［J］．农业机械学报，2006(3)：126-129．