小波神经网络研究

左东广，周 帅，张欣豫

(第二炮兵工程大学一系，西安 710025)

小波分析是20世纪80年代中期发展起来的一门新的数学理论和方法，是时间―频率分析领域的一种新技术。小波分析的基本思想类似于傅里叶变换，用信号在一簇基函数张成的空间上的投影表征该函数。神经网络起源于20世纪40年代，是由大量的、简单的处理单元(神经元)广泛地互相连接形成的复杂网络系统，它反映了人脑功能的许多基本特征，是一个高度复杂的非线性动力学系统［1］。由于小波变换能够反映信号的时频局部特性和聚焦特性，而神经网络在信号处理方面具有自学习、自适应、鲁棒性、容错性等能力。如何把二者的优势结合起来一直是人们所关心的问题，而小波神经网络就是小波分析和神经网络相结合的产物。

1 小波神经网络的基本结构

小波变换被公认为傅里叶发展史上一个新的里程碑，它克服了傅立叶分析不能作局部分析的缺点，是傅立叶分析划时代发展的结果［2］。随着小波理论日益成熟，其应用领域也变得十分的广泛，特别是在信号处理、数值计算、模式识别、图像处理、语音分析、量子物理、生物医学工程、计算机视觉、故障诊断及众多非线性领域等，小波变换都在不断的发展之中。

神经网络是在现代神经学的研究基础上发展起来的一种模仿人脑信息处理机制的网络系统，它具有自组织、自学习和极强的非线性处理能力，能够完成学习、记忆、识别和推理等功能［3］。神经网络的崛起，对认知和智力本质的基础研究乃至计算机产业都产生了空前的刺激和极大的推动作用。

目前小波分析与神经网络主要有两种结合方式［4］:一种是“松散型”，如图1所示，即先用小波分析对信号进行预处理，然后再送入神经网络处理;另一种是“紧致型”，如图2所示，即小波神经网络(Wavelet Neural Network)或小波网络，它是结合小波变换理论与神经网络的思想而构造的一种新的神经网路模型。其方法是将神经网络隐含层中神经元的传递激发函数用小波函数来代替，充分继承了小波变换良好的时频局部化性质及神经网络的自学习功能的特点，被广泛运用于信号处理、数据压缩、模式识别和故障诊断等领域。“紧致型”小波神经网络具有更好的数据处理能力，是小波神经网络的研究方向。在图2中，有输入层、隐含层和输出层，输出层采用线性输出，输入层有m(m=1，2，…，M)个神经元，隐含层有k(k=1，2，…，K)个神经元，输出层有 n(n=1，2，…，N)个神经元。

根据基函数gk(x)和学习参数的不同，图2中小波神经网络结构可分如下三种形式［5］:

1)连续参数的小波神经网络。这是小波最初被提出采用的一种形式。令图2中基函数为

则网络输出为

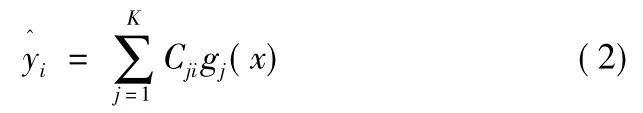
2)由框架作为基函数的小波神经网络。由于不考虑正交性，小波函数的选取有很大自由度。令图2中的基函数为

则网络输出为

根据函数f的时频特性确定j，k的取值范围后，网络的可调参数只有权值，其与输出呈线性关系，可通过最小二乘法或其他优化法修正权值，使网络能充分逼近f(x)。

这种形式的网络虽然基函数选取灵活，但由于框架可以是线性相关的，使得网络函数的个数有可能存在冗余，对过于庞大的网络需考虑优化结构算法。

3)基于多分辨分析的正交基小波网络。网络隐节点由小波节点Ψ和尺度函数节点φ构成，网络输出为

当尺度L足够大时，忽略上式右端第二项表示的小波细节分量，这种形式的小波网络的主要依据是Daubechies的紧支撑正交小波及Mallat的多分辨分析理论［6］。

尽管正交小波网络在理论上研究较为方便，但正交基函数的构造复杂，不如一般的基于框架的小波网络实用。

2 小波神经网络的训练算法

小波神经网络最早是由法国著名的信息科学机构IRISA的Zhang Qinghua［7］等人1992年提出来的，是在小波分析的基础上提出的一种多层前馈模型网络，可以使网络从根本上避免局部最优并且加快了收敛速度，具有很强的学习和泛化能力。小波神经网络是用非线性小波基取代通常的非线性sigmoid函数，其信号表述是通过将所选取的小波基进行线性叠加来表现的［8］。

3)对于预制光缆长度较短的工程应用，由于预制光缆长度可精准控制，推荐采用双端预制光缆；对于控制室与场地端(含二次预制舱及智能控制柜)间的预制光缆，由于控制室端熔接环境好，推荐采用单端预制光缆；对于场地端间的预制光缆，由于双端均不具备良好熔接环境的预制光缆，建议采用双端预制光缆。

设小波神经网络有m个输入节点、N个输出节点、n个隐层节点。网络的输入和输出数据分别用向量X和Y来表示，即:

若设xk为输入层的第k个输入样本，yi为输出层的第i个输出值，wij为联接输出层节点i和隐含层节点j的权值，wjk为连接隐含层节点j和输入层节点k的权值。令wi0是第j个输出层节点阈值，wj0是第j个隐含层节点阈值(相应的输入x0=－1)，aj为第j个隐含层节点的伸缩因子，bj为第j个隐含层节点的平移因子，则小波神经网络模型［9］为

给定样本集 { (xi，yi)}，i=1，2，…，N 后，网络的权值被调整，使如下的误差目标函数达到最小

式中:di为网络的输出向量;W为网络中所有权值组成的权向量，W∈Rt。网络的学习可以归结为如下的无约束最优化问题:

小波神经网络采用梯度法，即最快下降法来求解该问题，那么小波网络的权值的调整规则处理过程分为两个阶段:一是从网络的输入层开始逐层向前计算，根据输入样本计算各层的输出，最终求出网络输出层的输出，这是前向传播过程;二是对权值的修正，从网络的输出层开始逐层向后进行计算和修正，这是反向传播过程。两个过程反复交替，直到收敛为止。通过不断修正权值W，使E(W)达到最小值。

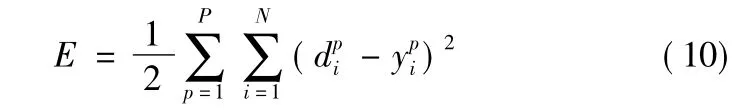
则由以上式子可以计算得到下列偏导数:

在网络权值的调整过程中，往往是在学习的初始阶段，学习步长选择大一些，以使学习速度加快;当接近最佳点时，学习速率选择小一些，否则连接权值将产生振荡而难以收敛。学习步长调整的一般规则是:在连续迭代几步过程中，若新误差大于旧误差，则学习速率减小;若新误差小于旧误差，则增大学习步长。

3 小波神经网络结构设计

3.1 小波函数的选择

小波的选择具有相对的灵活性，对不同的数据信号，则需要选择恰当的小波作为分解基。小波变换不像傅里叶变换是由正弦函数唯一决定的，小波基可以有很多种，不同的小波适合不同的信号。

1)Mexican hat和Morlet小波基没有尺度函数，是非正交小波基。其优点是函数对称且表达式清楚简单，缺点是无法对分解后的信号进行重构。采用Morlet小波(r通常取值为1.75)构造的小波网络已经被用于各种领域。

2)Daubechies是一种具有紧支撑的正交小波，随着N的增加，dbN小波的时域支撑长度变长;矩阵阶数增加;特征正则性增加，幅频特性也越接近理想。当选取N值越大的高阶db小波时，其构成可近似看成一个理想的低通滤波器和理想的带通滤波器，且具有能量无损性。

通常在信号的近似和估计作用中，小波函数选择应与信号的特征匹配，应考虑小波的波形、支撑大小和消失矩阵的数目。连续小波基函数都在有效支撑区域之外快速衰减。有效支撑区域越长，频率分辨率越好;有效支撑区域越短，时间分辨率越好。如果进行时频分析，则要选择光滑的连续小波，因为时域越光滑的基函数，在频域的局部化特性越好。如果进行信号检测，则应尽量选择与信号波形相近似［10］的小波。

3.2 隐含层节点的选取

隐含层节点的作用是从样本中提取并存储其内在规律，每个隐含层节点有若干个权值，而每个权值都是增强网络映射能力的参数。隐含层节点数量太少，网络从样本中获取信息的能力就差，不足以概括和体现训练集中的样本规律;隐含层节点数量太多，又可能把样本中非规律性的内容也会牢记，从而出现所谓的“过拟合”问题，反而降低了网络的泛化能力。此外，隐含层节点数过多会增加神经网络的训练时间。

4 仿真与结果分析

采用指数函数验证小波神经网络的数据拟合能力，自变量范围为［－5，5］，采样间隔为0.1，共101个样本点，其中前70个样本点作为训练样本，后31个样本点作为检验样本。小波神经网络采用“紧致型”结构，将神经网络隐含层中的神经元传递函数用小波函数来代替，采用通常用于信号分类的小波基函数Morlet小波函数(r通常取值为1.75)作为网络隐含层的激励函数，即:

式中，t为函数的输入，其小波函数的图形如图3。

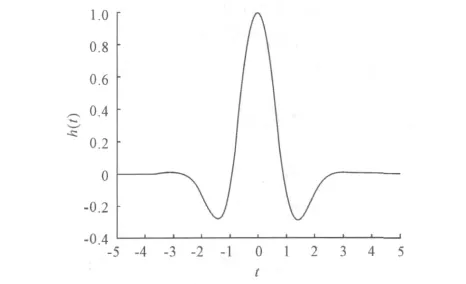
图3 Morlet小波函数

经过Matlab编程仿真得到的指数函数的逼近结果如图4。从预测结果来看，小波神经网络具有拟合能力较强，计算速度较快，精度高等优点，具有广泛的应用前景，但是该算法还存在着网络权值、尺度因子和平移因子的初值选取困难等缺点，这有待于进一步的研究。

图4 小波神经网络的预测结果

5 结束语

小波神经网络是小波分析和神经网络理论相结合的产物，继承了小波变换良好的时频局部化性质及神经网络的自学习功能的特点，它最初应用于函数逼近和语音识别，随后应用领域逐渐推广到非参数估计、天气预报、多属性决策、故障诊断与检测、系统辨识、数据压缩等。虽然小波分析理论和神经网络理论为小波网络的研究应用提供了坚实的理论基础，但小波网络的理论研究毕竟刚刚起步，迄今还存在许很大的发展空间。

［1］ 董长虹.matlab神经网络与应用［M］.北京:国防工业出版社，2007.

［2］ 张红英，吴斌.小波神经网络的研究及其展望［J］.西南工学院学报，2002(1):8－10.

［3］ 王永庆.人工智能原理与方法［M］.西安:西安交通大学出版社，1998.

［4］ 虞和济.基于神经网络的智能诊断［M］.北京:冶金工业出版社，2000.

［5］ 李洋.小波过程神经网络相关理论及其应用研究［D］.哈尔滨:哈尔滨工业大学，2008.

［6］ 秦前清，杨宗凯.实用小波分析［M］.西安:西安电子科技大学出版社，1998.

［7］ Zhang Qinghua，Bmvenlste A.Wavelet networks［J］.IEEE Trans.On Nellml Networks.1992，3(6):889 －898.

［8］ 王鸿斌，陈惠明.一种小波神经网络的优化算法［J］.忻州师范学院学报，2006(2):40－42.

［9］ 许慧，申东日.一种用于非线性函数逼近的小波神经网络［J］.自动化与仪器仪表，2003(6):4－6.

［10］侯木舟.基于构造型前馈神经网络的函数逼近与应用［D］.长沙:中南大学，2009.

［11］高隽.人工神经网络原理及仿真实例［M］.北京:机械工业出版社，2003.

(责任编辑周江川)