弹性体振动主动控制技术的研究现状

魏广威，王汉平，杨 鸣，王绍助，王林鹏

(北京理工大学 宇航学院，北京 100081)

在航空系统中，飞行器的气动弹性会引起一系列的振动，如自激振动引起的蒙皮颤振、翘曲发散、跨音速区因气流分离而产生的强迫振动即抖振效应等，例如德国的V－2导弹在荷兰的普里伯特˙马萨试验时就多次发生因蒙皮颤振而引起的事故。推力偏心、质量偏心以及阵风、紊流、气动力等各种不对称因素也都会使导弹在飞行过程中产生弹性振动(弯曲)，从而加大了导弹的攻角和偏角，对其控制系统性能造成一定程度的影响，弹性振动引起的弹体失稳而发生的事故有很多。如某弹道式导弹在设计稳定系统时，将弹看成了绝对刚体，没有考虑弹的弯曲振动的影响，结果在靶场试验时，在飞行的第8 s钟，导弹由于失稳而严重偏离弹道，在最后60 s落地坠毁。在关世义译的文献中列举了20种飞机和21种导弹的失稳事例，可以说明这一问题的严重性和研究意义［1］;随着大长径比导弹的发展，长径比的增加使得导弹的抗弯刚度和横向振动的固有频率降低，在发射过程中也会产生横向弯曲振动，会引起起始扰动，而且弹身的振动将给整个导弹系统带来一系列影响，导致导弹所携带仪器的工作精度下降、影响控制系统的控制精度，影响发射特性、飞行特性以及射击精度等等，这些影响叠加在一起最终会影响到导弹的技术战术性能，严重时甚至会直接导致导弹的损毁。Choi H D研究了KSR(Korea Sounding Rocket)－II型两级音速火箭的控制问题，该型火箭长径比达到26，箭体的弹性振动相当明显，他们通过研究发现弹性振动会通过反馈通道叠加到控制器的输出上，从而对控制系统的稳定运行造成影响，甚至导致系统不稳定，作者通过采用自适应滤波技术，在反馈通道中滤掉这种影响，从而保证系统的稳定性［2］。因此，弹性体导弹的振动主动控制问题已经成了必须要解决的问题，是振动控制要拓展应用的一个重要领域。

在航天领域，大型化、低刚度与柔性化是各类航天结构的一个重要发展趋势，这类大型柔性结构的模态阻尼小，对这些弹性体的振动进行主动控制更是必不可少的。以大型运载火箭为例，需要减振控制的部位很多，例如仪器仓，由于安装有火箭的控制、遥测等各种仪器，对振动环境有严格的要求;船箭或星箭接口支架，它传递发动机点火、级间分离等引起的对飞船或卫星的冲击，振动控制可以减少冲击对飞船或卫星的影响;飞船逃逸系统的栅格翼打开后，要保证飞船运动的稳定，振动控制是重要的保证措施。随着一些事故的发生，弹性体的振动控制越来越引起人们的关注和研究，所以，在航天航空领域，弹性体的振动控制是振动主动控制急需拓展的领域。

1 振动主动控制研究现状

1955年，美国科学家率先提出了振动主动控制技术的研究报告，进入上世纪70年代振动主动控制才进入广泛的探索阶段，如1972年Jnares等首先提出结构振动主动控制的概念，1979年国际理论和应用力学协会(IUTAM)召开了首届振动主动控制学会研讨会。尽管如此，上世纪70年代仍是被动控制技术占主导地位，振动主动控制技术只停留在研究和探索阶段，应用很有限。上世纪80年代，现代控制理论—尤其是随着信号处理技术的成熟，振动主动控制技术得到蓬勃发展。发展到上世纪90年代，振动主动控制技术已日趋成熟，其研究对象己经从简单的线性系统发展到复杂的非线性系统，控制系统从简单的单输入单输出发展到多输入多输出系统，控制方法也在不断改进，如近年来出现的模糊控制、神经网络控制等智能控制新型方法均有在振动主动控制中得到应用。

振动主动控制技术是指在振动控制过程中，根据所检测到的结构振动，应用一定的控制策略，经过适时计算，驱动作动器对结构施加某种影响，将结构振动控制在允许的范围以内。振动主动控制的控制方程是二阶常微分方程组，其一般形式:

式(1)中，M、C、K分别为系统的质量、阻尼、刚度矩阵，且均为n×n阶矩阵;p(t)、x(t)分别为系统的n维输入、输出向量，u(t)为施加于结构的控制力向量。主动控制的目的就在于寻求最佳的主动力u(t)，使结构在给定的输入情况下，其输出x(t)满足一定的要求。

下文就振动主动技术的研究现状，主要从作动器和控制律两方面进行分析:

1.1 振动主动控制中的作动器

对于主动控制系统，作动器是不可缺少的重要器件。传统型有液压作动、气压作动、电磁作动3种;新型的有压电陶瓷(PZT)、压电薄膜(PVDF)、电致伸缩陶瓷(ES)、形状记忆合金(SMA)、磁致伸缩合金(MS)、电流变流体(ERF)等6种。

振动主动控制技术研究的重点课题之一就是用主动控制技术控制弹性航天器结构的振动。利用机敏(智能)材料作为传感器和作动器元件控制弹性结构振动已引起广泛的关注，而压电智能材料以其优良的机电耦合特性被越来越多的应用于航空、航天器结构的振动主动控制当中，代表了目前研究和应用中的一个广阔而又活跃的领域。文献［3］提出了采用压电元件作为传感器和作动器，基于神经网络技术的柔性结构主动振动控制方法，对柔性梁在正弦和伪随机信号激励下的振动进行了主动控制实验，取得了较好的控制效果。David Ertur将压电作动器应用在柔性结构的振动控制中［4］。文献［5］使用压电作动器和PVDF薄膜做模态传感器对板振动进行主动控制试验。文献［6］利用压电陶瓷作为作动器采用独立模态控制法对柔性悬臂梁的前两阶模态实施主动控制，控制后明显增加了柔性悬臂梁的结构阻尼。EdwardF.Crawley给出了压电陶瓷与宿主结构作用的详细模型［7］。文献［8］以压电陶瓷作为作动器，研究表明基于主动振动控制方法设计的SRF补偿器可以大幅度地提高挠性结构振动模态的阻尼，抑制挠性结构的振动。文献［9］以多柔性机械臂为研究对象，采用PID模糊控制融合的方法建立控制系统，利用压电陶瓷作为作动器，搭建了实验平台，控制了柔性机械臂的弹性振动。Giurgiutiu介绍了压电晶片传感器在航空航天中的应用［10］。Suleman对压电作动器用于飞机的气动弹性振动控制的可行性进行了研究［11］。Hansson研究了压电单元用于火车体的竖向弹性振动控制［12］。文献［13］提出并设计制作了一种新颖的弓型压电作动器，将其应用在弹性梁振动主动控制中，实验结果表明这种弓型压电作动器具有良好的作动效能。

压电材料在目前的振动控制中使用比较广泛，其中压电材料的位置分布是目前振动主动控制中一个很活跃的研究课题。Ning采用遗传算法研究了结构主动振动控制中压电作动器的最优数量和位置问题［14］。Li Y等以控制系统能耗最大为基础，提出了一种新的同时考虑压电致动器/传感器和控制器反馈增益优化方法［15］。Kumar K等将压电致动器/传感器位置描述为零一优化问题，以 LQR控制系统的性能指标函数最小化为目标函数用遗传算法求解零一问题，获得了致动器/传感器的最优位置［16］。Roy等首先基于系统可控性指标采用遗传算法获得了压电致动器/传感器的最优位置，进而又以闭环系统阻尼比为目标函数研究了最优控制器中权矩阵的优化［17］。

1.2 振动主动控制技术算法

主动控制的算法决定了控制系统是否能达到预期控制效果，不同的环境条件、不同的要求精度、不同的控制对象要求的控制算法有所不同，振动主动控制器的控制算法列举如下，其中就模糊控制、神经网络等智能控制进行了详细论述。

传统的控制算法主要有以下几种:

1)独立模态空间控制方法。将无限自由度系统转化为在模态空间内少量几个模态的控制，即把具有分布参数特征的弹性体离散化为模态序列，通过控制振动的主模态对弹性体进行控制。Baz和Poh研究提出了用少于受控模态的作动器实现模态控制的修正的独立模态空间控制方法［18］。

2)最优控制法。它是现代控制理论中的控制方法，用极值原理、最优滤波、动态规划、随机分析原理等最优化方法设计控制算法。Hsiao利用最优控制在模态空间中得到了较好的结果［19］。Huang利用一种新的最优控制方法，减少了实时计算量［20］。

3)自适应控制法。自适应控制可分为自适应前馈控制、自校正控制和模型参考自适应控制，自适应控制的研究对象是具有不确定性的系统，被控对象的数学模型不是完全确定的，其中包含一些未知因素和随机因素。Rodellar研究了混合结构系统的直接自适应控制方法［21］。

4)直接输出反馈和前馈控制。直接输出反馈可以避免独立模态空间控制方法中的模态溢出等问题，但是控制系统是否稳定则存在争议，R.L.Clark认为控制系统如果考虑传感器件动力学和电路信号放大、调节的情况，控制系统将面临稳性、鲁棒性的问题［22］。前馈控制的作用是从扰动施加到系统时开始的，要比反馈控制系统反应快。Sungkook KANG指出只有在扰动的动态特性已知时，前馈控制的作用才是显著的［23］。

5)极点配置法。它是根据对被控系统动态品质的要求，确定系统特征值与特征向量的分布，通过状态反馈或输出反馈来将系统的闭环极点放在复平面中预定的位置，从而实现预定的要求。文献［24］在常规极点配置法的基础上，提出了同时优化系统极点和传感器/作动器位置的联合优化设计方法。

实际应用的弹性体结构一般是一个非线性时变动态系统，通过理论分析建立较为准确的动力学模型十分困难，如在弹性体导弹主动减振控制领域，振动主动控制应用还不是很广泛，原因主要有两点:其一是现有导弹振动大都仍在容许的范围内，且工程上更偏向于从材料和结构上解决导弹的振动问题;其二是从减振控制的角度进行减振设计本身存在诸多难点，它首先要求精确的描述弹体的整个耦合关系，由于导弹的横向振动受到各种因素影响，这种耦合关系的描述较为困难。所以急需解决具有不确定性、非线性、时变和滞后的复杂系统的建模与控制问题，传统的振动控制方法在这一领域受到了严重的挑战，从而要求人们探索新的振动控制方法。故一些新型的控制算法就得到了蓬勃发展，也是近期主动控制领域研究的重点。目前弹性体振动控制律研究较多的主要有模糊控制、H∞鲁棒控制、神经网络控制等，下面就这些控制算法的研究进行分析。

鲁棒控制选择线性反馈律，使得闭环系统的稳定性或性能对于扰动具有一定的抵抗能力。当系统有一个小扰动时，实际模态可能发生很大的变化，必须考虑鲁棒性问题。Liu等人利用μ理论研究了结构中刚度参数含不确定性的鲁棒控制问题［25］。Nishitani给出了使用降阶模型的H∞结构响应控制。H∞控制将鲁棒性直接反映在控制性能指标上，设计出的控制律具有其他方法无可比拟的稳定鲁棒性［26］。Friang J P探讨了弹性体导弹的弹性变形环节所带来的参数不确定性问题以及建模不确定性问题，用H∞回路成形方法设计鲁棒控制方案，并对系统性能进行了分析［27］。文献［28］运用附加作动力进行主动减振，提出了弹性体导弹主动减振组合控制方案，仿真分析了控制器的减振效果。他们针对解耦的刚性子系统设计H∞控制器模拟弹性体导弹的刚体控制器，针对弹性子系统设计LQR控制器，再基于耦合关系对H∞控制器和LQR控制器进行组合，得到主动减振组合控制器。

模糊控制是智能控制的一个重要分支，模糊控制理论的产生和发展为振动主动控制带来了新的活力，它不仅提供系统的客观信息，而且可以将人类的主观经验和直觉纳入控制系统，这就为非线性、存在不确定因素、难以建立精确数学模型的复杂系统进行振动主动控制提供了更为有力的理论方法。模糊控制直接采用语言型控制规则，在设计中不需要建立被控对象的精确数学模型。模模糊控制系统的鲁棒性强，干扰和参数变化对控制效果的不利影响被大大减弱，尤其适合于非线性、时变及纯滞后系统的控制。

模糊控制系统的组成类似于一般的数字控制系统，组成如图1所示。

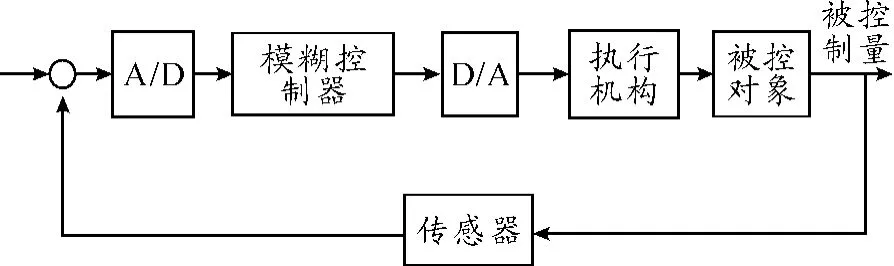
图1 模糊控制系统的原理

模糊控制器的控制是通过微机采样获取被控制量的精确值，然后将此量与给定值比较得到误差信号E，把误差信号E的精确量进行模糊化成模糊量，误差E的模糊量可用响应的模糊语言来表示，由误差E的模糊语言集合的一个子集e和模糊控制规则R根据推理合成规则进行决策，得到模糊控制量u

式(2)中u是一个模糊量。在模糊控制理论中，由于被控对象的不同，以及对系统静态、动态特性的要求和所应用的控制策略的不同，可以构成各种类型的控制器:如Fuzzy-PID复合控制，常见的是Fuzzy-PI双模控制形式;参数自整定模糊控制;模型参考自适应模糊控制;自组织模糊控制;具有自学习功能的模糊控制;多变量模糊控制等。

自从L.A.Zadeh首先提出了用模糊集合描述事物以来，模糊数学及应用的发展十分迅速，为解决不易或无法建模的复杂系统控制问题提供了有力的手段，模糊技术在振动控制中得到了较广泛的应用。Joghataie A利用模糊推理规则改进神经元网络控制器［29］。文献［30］将模糊控制与优化方法相结合，提出转子系统横向振动的模糊控制方法。文献［31］将模糊控制和PI控制相结合应用于压电挠性结构的振动主动控制，采用Fuzzy-PI双模控制方法，对瞬态激励作用下挠性悬臂梁的振动主动控制问题进行了研究。文献［32］在已有模糊控制和自适应方法相结合的控制基础上，提出了一种基于模糊逻辑的自适应前馈振动控制方法，针对柔性悬臂梁结构的仿真计算结果表明模糊自适应前馈滤波达到了预期的控制效果。文献［33］提出了一种模糊自整定PID算法，将模糊控制和PID控制结合起来，构成一个模糊自整定PID控制器，通过模糊控制规则在线调整PID控制器参数，自动实现对PID参数的最佳整定，从而实现柔性机械臂的振动主动控制。文献［34］结合模糊控制方法智能化的特点，设计出一种不依赖模型参数且可以自动调节控制器增益的控制算法，试验表明，模糊变增益控制方法保留了普通PID控制的稳定性能，并且结合模糊控制方法智能化的特点，使系统具备了更强的适应能力和适用范围。Qu Wenzhong在柔性结构上研究了自适应模糊振动主动控制算法的有效性。试验中采用了两种模糊控制器，一种模糊控制器用来辨识柔性结构非线性系统的误差通道，抑制参考信号对非线性系统的扰动;另一种模糊控制器通过非线性压电作动器进行振动主动控制。试验结果表明了这种控制算法的有效性［35］。Gustavo Luiz C.M.de Abreu和Jose F.Ribeiro以压电材料作为传感器利用自组织模糊控制算法对柔性结构进行振动主动控制研究。试验结果表明对于复杂系统这种控制策略能方便地执行，粘连在柔性结构上的压电作动器能对复杂结构进行控制且控制效果在预先设计的范围内［36］。目前模糊振动控制取得了一定的研究成果，也存在一些问题，如精度不太高，自适应能力有限，易产生震荡现象等，为进一步应用带来了挑战，同时也带来了研究的动力。

智能控制中最具代表性的就是神经网络控制，作为智能控制的一个重要分支，在“黑箱”系统的辨识与非线性控制方面表现出巨大的潜力。神经网络能大规模并行分布处理非线性系统，故在更高层次上体现了人类的智能行为。而控制系统所面临的愈来愈严重的挑战促进了神经网络控制的发展，目前这一研究正蓬勃发展、方兴未艾。

神经网络是指利用工程技术手段模拟人脑神经网络的结构和功能的一种技术方法。神经网络具有高度自适应学习能力、鲁棒性、容错性和自组织离散分布处理能力，不仅可以用于系统模型的辨识，也可用于系统振动控制，对于非线性具有很强的逼近或映射能力，尤其适用于描述复杂非线性系统。在实时控制中，由于神经网络运算过程中误差的反复计算和迭代过程计算量很大，会遇到耗时过长问题，因此较适用于大型复杂结构。目前控制中常用的神经网络为多层前馈神经网络(BP网络)。

目前已将神经网络和模糊技术互相结合，取长补短，形成了一种模糊神经网络技术，由此组成一种更接近人脑的智能信息处理系统。由于神经网络控制有其他控制法所不具有的优点，故在工程上得到了广泛的应用。文献［37］将最优控制算法与人工神经网络相结合，采用BP神经网络模型，实现了受随机波浪力作用下的海洋平台的振动主动控制。文献［38］采用基于神经网络的间接自适应控制策略对弹性连杆机构实施了振动主动控制，设计了神经网络辨识器与神经网络控制器，取得了比较理想的减振效果。Kavous Jorabchi等人基于多层前馈神经网络，采用反馈线性化控制方法(NARMA－L2模型)对智能尾翼结构减振系统进行辨识和控制，并通过闭环测试跟PID控制器进行控制效果的比较［39］。文献［40］采用间接神经参考模型自适应控制方法对悬臂梁结构进行了振动主动控制研究。文献［41］采用线性人工神经网络对系统动态特性进行在线辨识，并利用辨识得到的信息，采用BP神经网络对系统进行控制，将该算法应用于飞机机翼振动主动控制数值仿真。文献［42］分别利用模态控制法和神经网络模型参考控制方法对简支梁进行振动主动控制，并进行了计算机仿真和实验验证。文献［43］以某型飞行器的垂尾模型为研究对象，利用人工神经网络进行了垂尾结构控制系统的非线性振动模型辨识和振动主动控制研究和实验。

2 主动控制技术展望

现有的振动主动控制技术的发展虽然取得了一些成果，但是还有一些理论和技术问题需要进一步的研究和探索。

1)研究智能主动控制算法，如连续分布系统的控制方法、存在非线性特性和结构的时变不确定性系统的控制方法。随着系统越来越复杂，传统控制算法受到很大限制，需要发展智能控制技术，如神经网络、模糊控制等，而智能控制技术在振动主动控制中亦尚有许多问题亟待解决。

2)要实现更精确的控制，开发高精度、智能化传感器、作动器和集成化传感作动部件已成必然之势，而压电材料具有正逆压电耦合效应，这使得其既可作为感知外部环境变化的传感器，又可作为对外部环境变化作出迅速反应调整结构自身适应能力的致动器，压电材料是发展的趋势。

3)结构控制一体化优化技术，即将传感器、作动器、控制器等有机地与结构集成。主动改变结构自身刚度和阻尼分布，自适应实现振动控制的目标。智能结构设计应综合结构设计，传感器、作动器设计及其配置、控制器设计等环节联合进行。这种智能结构在航空、航天、建筑等工程中有着广泛的应用前景。

［1］ 关世义译.关于气动弹性引起的飞行器控制系统丧失稳定性的调查［J］.外国海军导弹科技动态，1978(10):52－54.

［2］ Choi H D，Bang H.An adaptive control approach to the attitude control of a flexible rocket［J］.Control Engineering Practice，2000，18(9):1003 －1010.

［3］ 路小波，陶云刚.基于神经网络的柔性结构振动主动控制研究［J］.振动工程学报，2000，13(1):107 －110.

［4］ David Ertur.Adaptive vibration isolation for flexible structures［J］.Journal of Vibration and Acoustics，1999 12(1):440－445.

［5］ Y.Gu，R.L.clark，C.R.Fuller.Experiments on Active Control of Plate Vibration Using Piezoelectric Actuators and Polyvinylidene Fluoride(PVDF)Model Sensors［J］.Journal of Vibration and Acoustics，Transactions of the ASME.July 1994，116:303 －308.

［6］ 吴大方，刘安成，麦汉超.压电智能柔性梁振动主动控制研究［J］.北京航空航天大学学报，2004，2(30:)160－163.

［7］ Edward F.Crawley，Eric H.Anderson.Detailed Models of Piezoceramic Actuation of Beams［J］.Journal of Intelligent Material Systems and Struetures，1990(1):101 －103.

［8］ 朱良宽，马广富.挠性航天器鲁棒反步自适应姿态机动及主动振动抑制［J］.振动与冲击，2009，28(2):132－136.

［9］ 周刚.PID模糊控制融合的压电柔性机械臂振动主动控制研究［D］.北京:北京工业大学工学，2007.

［10］ Giurgiutiu V，Zagrai A，Bao J.Piezoelectric Wafer Embedded Active Sensors for Aging Aircraft Structural Health Monitoring［J］.Structural Health Monitoring，2002，1(1):41－61.

［11］ Suleman A，Costa A.Adaptive control of an aeroelastic flight vehicle using piezoelectric actuators［J］.Computers ＆Structures，2004，82(17 －19):1303 －1314.

［12］ Hansson J，Takano M，Takigami T，et al.Vibration Suppression of Railway Car Body with Piezoelectric Elements［J］.JSME International Journal Series C，2004，47(2):451－456.

［13］杨智春，王巍.一种新型压电作动器及在结构振动主动控制中的应用［J］.机械强度，2008，30(5):735 －738.

［14］ Ning H.Optimal number and placements of piezoelectric patch actuators in structural active vibration control［J］.Engineering Computations，2004，21(6):651 －665.

［15］ Li Y，Onoda J，Minesugi K.Simultaneous optimization of piezoelectric actuator placement and feedback for vibration suppression［J］.Acta Astronautica，2002，50(6):335－341.

［16］ Kumar K，Narayanan S.Active vibration control of beams with optimal placement of piezoelectric sensor/actuator pairs［J］.Smart Materials and Structures，2008，17:055008.

［17］ Roy T，Chakraborty D.Optimal vibration control of smart fiber reinforced composite shell structures using improved genetic algorithm［J］.Journal of sound and vibration，2009，319(1－2):15－40.

［18］ Baz A，Poh S.Experimental Implementation of the Modified Independent Modal Space Control Method［J］.Journal of Sound and Vibration，1990，139(1):76 －79.

［19］ Min-Hung Hsiao.An Optimal Modal-Space Controller for Structural Damping Enhancements［C］//Maryland:Proceedings of the American Conf.，Baltimore，June，1994.

［20］ Shiuh-Jer Huang etc.Active Optimal Vibration Control for a Lumped System［J］.Computers ＆ Structures，1994，51(6):45－47.

［21］ Rodellar J.Response analyses of buildings with a new nonlinear base isolation system［C］//Los Angeles:Proc.First World Conf on Struct Control，1994:31 －40.

［22］ Clark R L.Moving Away from Collocated Control［J］.J.of Sound ＆ Vib，1996，190(1):81 －83.

［23］ Sungkook KANG etc.Criterion Functions and Their Control Characteristics for Active Vibration Control［J］.JSME International Journal，Series C，1994，37(3):89 －91.

［24］陈大跃，胡宗武，范祖尧.振动控制的特征结构配置［J］.振动工程学报，1991，2(2):75 －81.

［25］ Liu D D，Mao J Q，Zhang J.Structure control with stiffness uncertainty in earthquake zone［C］//Italy:IEEE International Conf.on Control App，1998.

［26］ Nishitani A.H∞structural response control with reduced-order controller［C］//Los An-geles:Proc.First World Conf.Struct.Control，1994，TP4:63 －72.

［27］ Friang J P，Gilles D，Bonnet J P.Robust autopilot for a flexible missile:Loop-Shaping H∞design and real analysis［J］.International Journal of Robust and Nonlinear Control，1998，18(2):129 －153.

［28］高强.弹性体导弹振动主动控制研究［D］.合肥:中国科技大学，2009.

［29］ Joghataie A.Neural networks and fuzzy logic in structural control［C］//Los Angeles:Proc.First World Conf.Struct.Control，1994，FA2:63 －72.

［30］ Yuan Y，Wen B C.Studies of a fuzzy control method for a rotor system transverse vibration［C］//Beijing:Proceeding of the International Conference on Vibration Engineering ICVE’94，1994:823 －827.

［31］魏井君，邱志成.基于模糊控制的压电挠性梁的振动主动控制实验研究［J］.振动与冲击，2008，27(12):91－96.

［32］侯新科，刘巍.基于模糊自适应控制的悬臂梁振动主动控制算法研究［J］.甘肃科学学报，2008，20(3):75－77.

［33］曹青松，周继惠.基于模糊自整定PID算法的压电柔性机械臂振动控制研究［J］.振动与冲击，2010，29(12):181－186.

［34］邵敏强，陈卫东.基于PID控制方法的模糊变增益振动主动控制试验研究［J］.南京航空航天大学学报，2012，44(1):20－24.

［35］ Qu Wenzhong，Sun Jincai，Qiu Yang.Active Control of Vibration using a fuzzy control method［J］.Journal of Sound and vibration.2004(275):917 －930.

［36］ Gustavo Luiz C.M.de Abreu，Jose F.Ribeiro.A Self-organizing fuzzy logic controller for the active control of flexible structures using piezoelectric actuators.Applied Soft Computing，2002(1):271 －283.

［37］周亚军，赵德有.基于人工神经网络的海洋平台振动主动控制［J］.船舶力学，2003，7(5):65 －69.

［38］宋轶民，马文贵.基于神经网络的弹性连杆机构振动主动控制［J］.自动化学报，2000，26(5):660 －665.

［39］ Kavous Jorabchi，Aghil Yousefi-Koma.A Neural Network Controller for Vibration Suppression of a Smart Fin［C］//47th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference，2006(5):1 －4.

［40］王玉辉.基于神经网络的悬臂梁振动主动控制研究［D］.南京:南京航空航天大学，2005.

［41］李伟，童中翔.基于神经网络的机翼振动主动控制［J］.机械与电子，2004(9):56－58.

［42］吴召明.梁的振动主动控制技术研究［D］.北京:北京邮电大学，2006.

［43］孙丽华.基于神经网络的飞机垂直尾翼振动主动控制［D］.南京:南京航空航天大学，2010.

(责任编辑周江川)